Casos especiais - Lugar geométrico das raízes
Produzido por Alexandre NunesTeoria
Polos e zeros complexos
Um caso que ainda não vimos é como esboçar o lugar geométrico das raízes quando temos polos e/ou zeros complexos. A função de transferência abaixo é um exemplo desses casos:
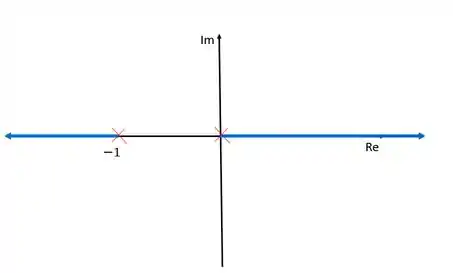
Essa função tem quatro polos, , e . Vamos expressá-los no diagrama de lugar das raízes:
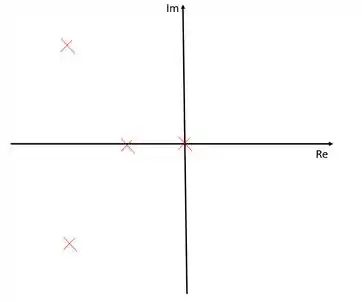
Temos esse par de polos complexos que não sabemos muito bem como lidar. Antes de começar a resolver esse problema, vamos fazer o que já sabemos. Temos quatro polos e nenhum zero, o que significa que precisamos de quatro zeros no infinito, ou seja, quatro assíntotas. Vamos calcular essas assíntotas como aprendemos na teoria de lugar das raízes.
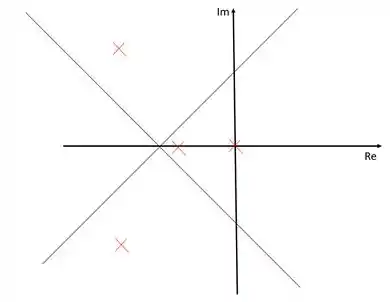
Uma das regras do lugar das raízes é que os ramos nascem nos polos e morrem nos zeros, sendo assim, podemos traçar os ramos nos polos que estão sobre o eixo dos reais:
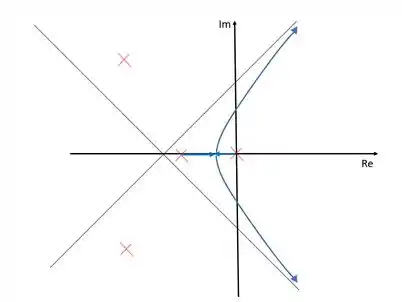
Os ramos, então, nascem nos polos e morrem nos zeros no infinito determinados pelas assíntotas, nada novo até aqui. A novidade é que os ramos não saem do eixo dos reais exatamente no meio do intervalo entre e . O que acontece é que os polos imaginários têm o efeito de “empurrar” o lugar das raízes para longe deles, e por isso, o ponto em que os ramos deixam o eixo dos reais está mais próximo de do que de .
Mais para frente vamos aprender a calcular esse ponto.
Agora precisamos esboçar os ramos que saem dos polos imaginários e tendem aos outros dois zeros no infinito. Para fazer esse esboço, precisaremos usar a propriedade de que a soma dos ângulos do lugar das raízes é um múltiplo ímpar de :
Isso quer dizer que a soma dos ângulos formados entre todos os polos e zeros em qualquer ponto do lugar das raízes é igual a um múltiplo ímpar de .
Para fazer o esboço, precisamos saber o ângulo com que o lugar das raízes sai do polo imaginário, para isso vamos calcular os ângulos de todos os polos com o polo imagiário:
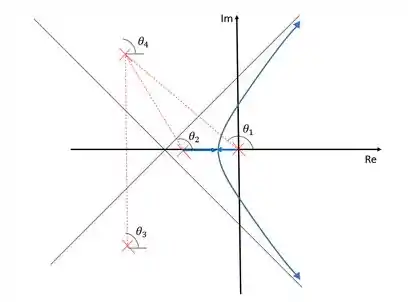
Uma vez que encontremos os ângulos , e , podemos calcular o ângulo .
Para esse caso, encontraremos , sendo assim, o ramo do lugar das raízes sai do polo imaginário formando um ângulo de e depois tende ao zero no infinito determinado pela assíntota.
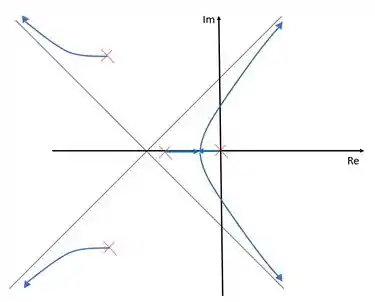
Pontos de saída e entrada sobre o eixo real e cruzamento com o eixo
Como vimos acima, nem sempre será direto a determinação do ponto onde o lugar das raízes deixa e chega no eixo dos reais.
Entretanto, existe um método bem direto de se determinar esses pontos.
Para determinar esses pontos, devemos maximizar/minizar a expressão para o ganho. A equação característica de um sistema é:
Isolando o ganho:
Para encontrar o ponto em que o lugar das raízes deixa o eixo dos reais devemos substituir por e depois encontrar os valores de que maximizam ou minimizam o ganho.
Em seguida, derivamos o ganho em relação a sigma e encontramos os valores de que satisfazem a igualdade:
Para determinar o ponto em que o lugar das raízes cruza o eixo dos imaginários (eixo ), podemos usar o método da substituição direta.
Esse método nos fornece o ganho e a frequência final, ou seja, o ganho e a frequência que tornam o sistema instável.
Sendo assim, o ponto que o lugar das raízes cruza o eixo dos imaginários é:
Se você não estiver com esse método fresquinho na cabeça, seria legal dar uma revisada nesse conteúdo.
Lugar das raízes com realimentação positiva
Vimos até agora, como esboçar o lugar das raízes quando temos um sistema com realimentação negativa.
Sistemas com realimentação negativa é o mais comum e o mais usado em controle de processos, entretanto, podemos encontrar casos de realimentação positiva, como no diagrama de blocos abaixo:
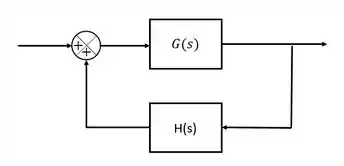
Esses sistemas, tem função de transferência do tipo:
O que muda é o sinal do denominador que em vez de ser “mais” será “menos”.
Para esses sistemas, todas as regras e conceitos da construção do lugar das raízes são as mesmas, com duas exceções:
- O lugar das raízes existe no eixo dos reais se estiver à esquerda de um número par de polos e zeros;
- A soma dos ângulos de partida é um múltiplo par de .
Além disso, para se calcular as assíntotas, as fórmulas para os ângulos das assíntotas também será alterada:
Pontos de saída e entrada sobre o eixo real e cruzamento com o eixo ω i
Lugar das raízes com realimentação positiva
Exercícios Resolvidos
Exercício Resolvido #1
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.3a
Esboce o lugar geométrico das raízes e suas assíntotas para um sistema de retroalimentação unitária com a seguinte função de transferência:
Passo 1
Vamos começar representando tanto os zeros como os polos da função de transferência em malha aberta no diagrama de lugar das raízes.
Para essa função de transferência temos dois zeros em e e dois polos em .
Passo 2
Neste caso o número de zeros finitos é igual ao número de polos infinitos, ou seja, não teremos zeros no infinito, e se não temos zeros no infinito, não precisamos calcular as assíntotas.
Além disso, como os polos estão exatamente no meio dos dois zeros, o lugar onde o rmo vai entrar no eixo dos reais é a metade do caminho entre e , ou seja, .
Desenhando os ramos:
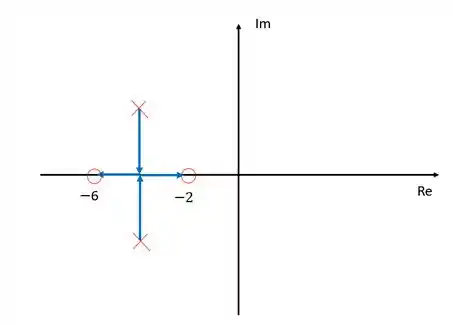
Nosso diagrama está obedecendo a todas as regras:
- Os ramos nascem nos polos e morrem nos zeros;
- O número de ramos é igual ao número de polos em malha aberta;
- Simetria em relação ao eixo dos reais existe;
- Só existe ramos sobre o eixo dos reais nos locais onde à esquerda existe um número ímpar de polos e zeros.
Portanto, nossa resposta está correta.
Resposta
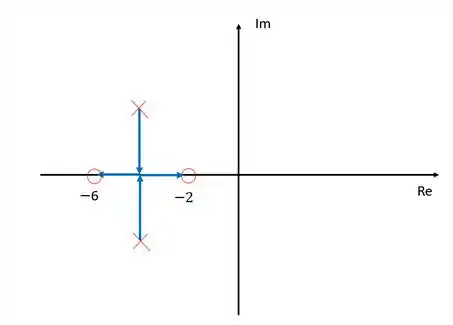
Exercício Resolvido #2
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.3b
Esboce o lugar geométrico das raízes e suas assíntotas para um sistema de retroalimentação unitária com a seguinte função de transferência:
Passo 1
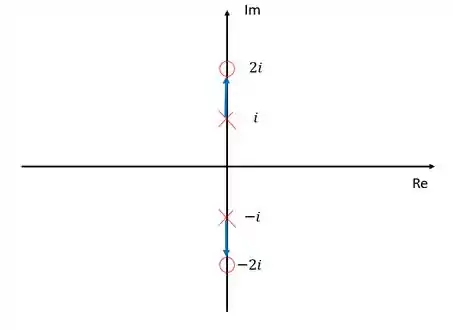
Nessa função de transferência temos dois polos complexos e dois zeros, também complexos. Tanto os polos como os zeros são complexos puros, sendo os polos e os zeros .
Vamos representa-los no diagrama de lugar das raízes:
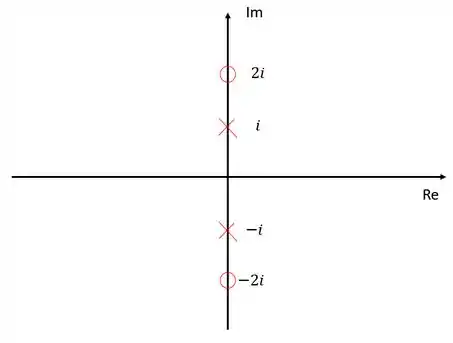
Passo 2
Neste caso o número de polos em malha aberta é igual ao número de zeros em malha aberta, snedo assim, não precisaremos calcular as assíntotas, pois não teremos zeros no infinito.
Além disso, tanto os polos quanto os zeros se encontram sobre o eixo dos imaginários, e pelo arranjo que eles se encontram, podemos perceber que os ramos jamais cruzarão o eixo dos reais. Sendo assim, se seguirmos todas as regras, já podemos esboçar o diagram de lugar das raízes para essa função de transferência.
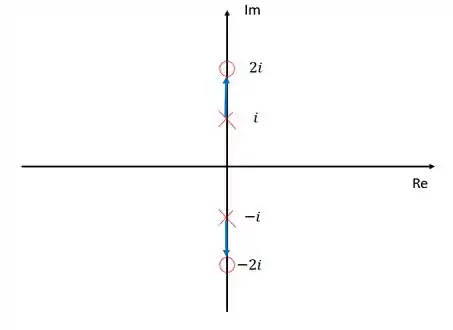
Vamos conferir se todas as regras foram atendidas:
- Os ramos nascem nos polos e morrem nos zeros;
- O número de ramos é igual ao número de polos em malha aberta;
- Simetria em relação ao eixo dos reais existe;
- Só existe ramos sobre o eixo dos reais nos locais onde à esquerda existe um número ímpar de polos e zeros (não vem ao caso porque não temos ramos sobre o eixo dos reais).
Portanto, nossa resposta está correta.
Resposta
Exercício Resolvido #3
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 8.3
Determine os pontos de entrada e saída do lugar de saída de um sistema com realimentação unitária e função de transferência:
Passo 1
Para obter os posntos de entrada e saída, primeiramente devemos encontrar a expressão para , para em seguida poder maximizá-la/minimizá-la:
Isolando :
Passo 2
Agora só precisamo substituir por e derivar a expressão encontrada:
Passo 3
Para encontrar os pontos onde o lugar das raízes entra/sai do eixo real, precisamos maximizar/minizar a função , ou seja, encontrar os valores de que anulam a sua derivada.
Sendo assim:
Resposta
Exercício Resolvido #4
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.6
Considere um sistema com realimentação unitária e função de transferência mostrada abaixa.
Esboce o lugar as raízes e diga para quais valores de , o sistema é instável.
Passo 1
Primeiramente, vamos representar os polos e zeros no diagrama de lugar das raízes.
A função de transferência tem dois zeros: e , e dois polos: e .
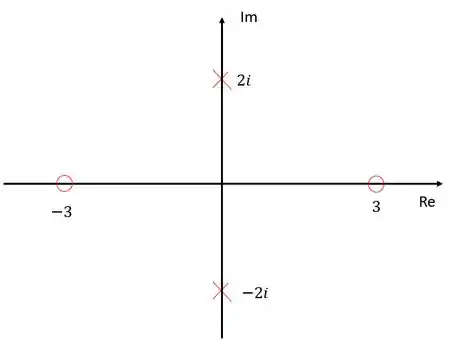
Passo 2
Agora vamos fazer nosso nosso esboço.
Devemos nos lembrar que os ramos nascem nos polos e morrem nos zeros, e que a simetria com relação ao eixo dos reais deve ser obedecida.
Além disso, os ramos só podem existir sobre os eixos dos reais se a esquerda dele houver um número ímpar de polos e zeros.
Como os polos se enontram exatamente no meio do caminho entre os dois zeros, podemos garantir que os ramos vão entrar no eixo dos reais exatamente no meio do intervalo entre os dois zeros.
Tendo tudo isso em mente, já podemos esboçar nosso diagrama:
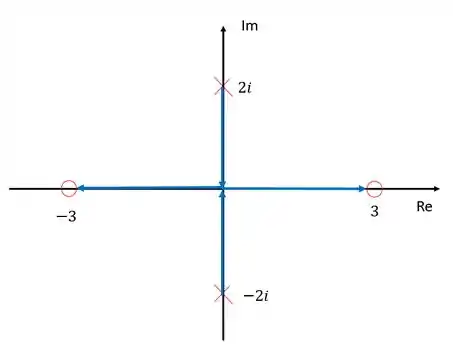
Passo 3
Agora, precisamos encontrar qual valor de faz com que o sistema fique instável. Vamos analisar a equação característica do sistema:
Para que o sistema seja estável, todos os termos devem ter o mesmo sinal. Não existe nenhum valor de que faça ambos os termos ficarem negativos, então vamos avaliar os valores de que faça os termos ficarem positivos:
Como no lugar das raízes trabalhamos com valores de que vão de até , podemos dizer que o sistema é instável para:
Resposta
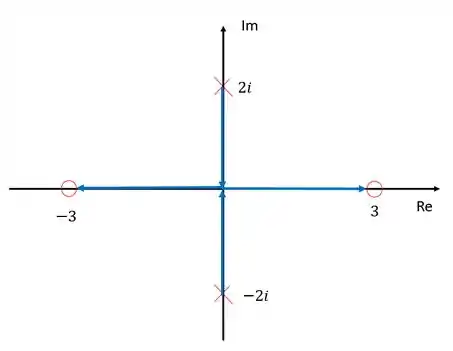
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.6
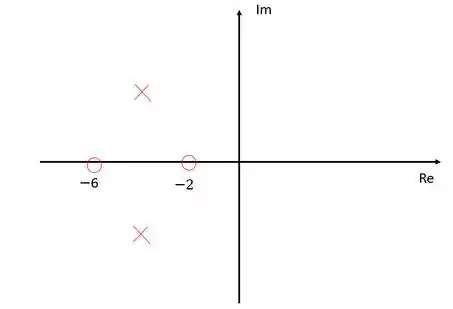
Para o diagrama de polos e zeros em malha aberta mostrado na figura abaixo, esboce o lugar geométrico das raízes e determine o ponto de entrada.
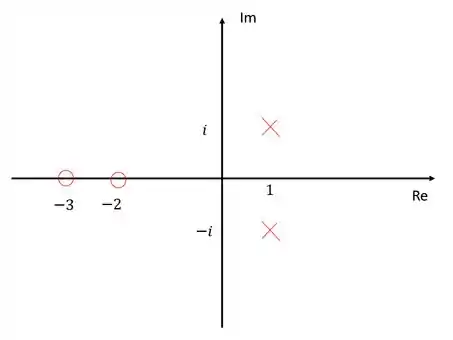
Passo 1
Temos então um diagrama de lugar das raízes de uma função de transferência em malha aberta com dois polos e dois zeros, sendo os zeros e , e os polos, .
Vamos então escrever a função de transferência para esse diagrama:
Passo 2
Nessa função temos dois polos e dois zeros, o que quer dizer que não teremos nenhum zero no infinito, então, não precisamos calcular as assíntotas.
Entretanto existem outras duas coisas que precisamos saber para fazer um bom esboço do diagarama de lugar das raízes: em que ponto o diagrama entre no eixo dos reais e com qual ângulo os ramos saem dos polos.
Se pensarmos um pouco sobre as regras que dizem que os ramos saem dos polos e morrem nos zeros, e que o diagrama é simétrico em relação ao eixo dos reais, poderemos imaginar que os ramos vão sair do polo e entrar no eixo dos reais em algum ponto entre os dois zeros, mas não sabemos com que ângulo essa saída se dá nem em que ponto eles entram no eixo dos reais.
Passo 3
Vamos começar pelo ponto de entrada.
Para isso, devemos maximizar\minimizar na expressão:
Isolando :
Substituindo por , e derivando em relação a , teremos:
Os valores de que satisfazem essa igualdade são e . Como o ponto de entrada está entre os dois zeros, o valor que nos satisfaz é .
Passo 4
Agora devemos encontrar o ângulo com que os ramos saem dos polos, para isso precisamos fazer a soma de todos os ângulos, o resultado deve ser um múltiplo ímpar de .
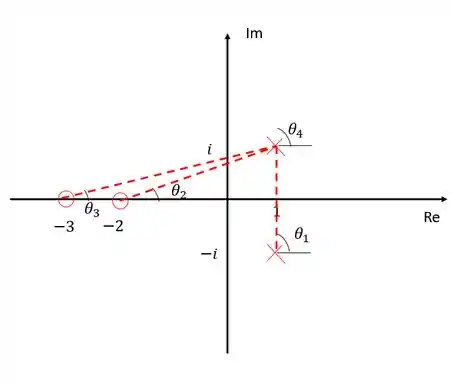
Para achar basta somar tudo e encontrar um ângulo cuja a soma seja um múltiplo ímpra de . Lembre-se sempre que os polos contribuem positivamente e os zeros negativamente:
Passo 5
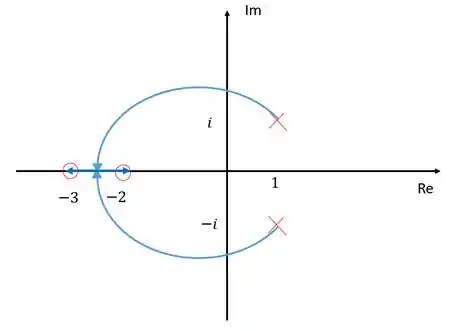
Agora já podemos fazer nosso esboço:
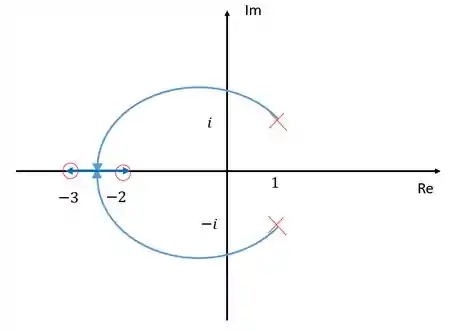
Resposta
Exercício Resolvido #6
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.14a. Adaptado
Esboce o lugar geométrico das raízes para um sistema com realimentação unitária e a seguinte função de transferência em malha aberta:
Passo 1
Primeiramente, vamos marcar no nosso diagrama todos os zeros e polos:
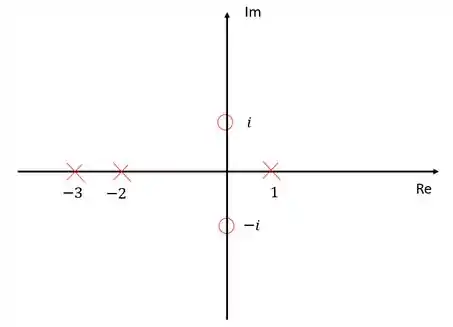
Passo 2
Temos um polo a mais que zero, o que significa que precisamos calcular uma assíntota que indique onde se encontra o zero no infinito.
Termos então uma assíntota com ângulo de que se encontrará sobre o eixo dos reais. Sendo assim, não precisamos calcular o ponto de interseção dessa assíntota sobre o eixo.
Passo 3
Vamos agora calcular o ponto em que o lugar das raízes deixa o eixo dos reais. Para isso precisamos maximizar na expressão:
Substituindo por , e derivando em relação a :
Existem dois valores para que satisfazem a igualdade: e , entretanto, não pode existir lugar das raízes em pois à esquerda desse ponto existem dois polos, e a condição para que exista lugar das raízes sobre o eixo real é que à esquerda deve existir sempre um número ímpar de zeros e polos.
Portanto, o lugar das raízes sairá do eixo dos reais em e para fins de esboço e práticos, vamos aproximar esse valor para .
Passo 4
Agora devemos encontrar o ângulo com que os ramos saem dos polos, para isso precisamos fazer a soma de todos os ângulos, o resultado deve ser um múltiplo ímpar de .
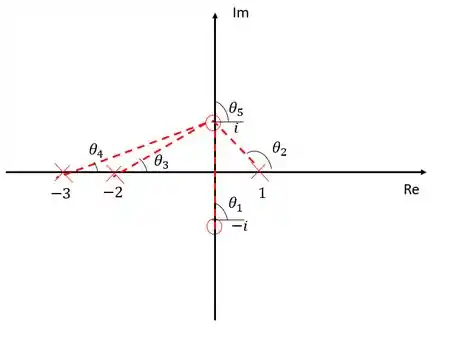
Para achar basta somar tudo e encontrar um ângulo cuja a soma seja um múltiplo ímpra de . Lembre-se sempre que os polos contribuem positivamente e os zeros negativamente:
Passo 5
Agora já podemos fazer nosso esboço:
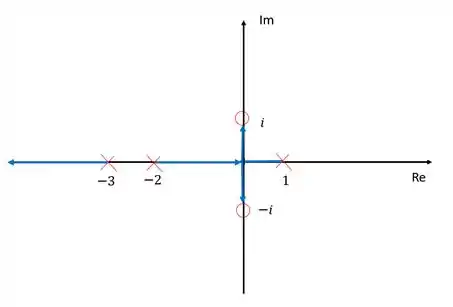
Os ramos que saem dos polos e saem do eixo dos reais em e morrem nos dois zeros finitos fazendo um ângulo de e .
Além disso, o ramo que nasce no em tende a infinito conforme a assíntota que calaculamos.
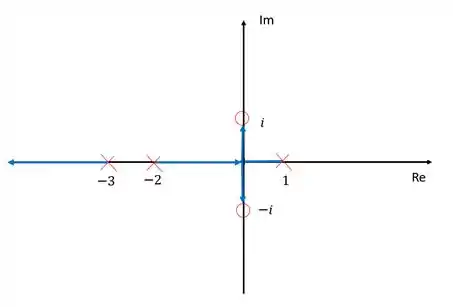
Resposta
Exercício Resolvido #7
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Problema 8.24. Adaptado
Esboce o lugar geométrico das raízes para um sistema com realimentação unitária positiva e a seguinte função de transferência em malha aberta:
Passo 1
Trata-se de um sistema com realimentação positiva, isso quer dizer que todas as regras que usamos até aqui são válidas com exceção de duas: o lugar das raízes existe no eixo dos reais se à sua esquerda existir uma quantidade par de polos e zeros, e a soma de todos os ângulos em qualquer ponto do lugar das raízes é um múltiplo par de .
Vamos começar, como sempre, representando os nossos polos e zeros no diagrama. Ness exercício temos dois polos: e .
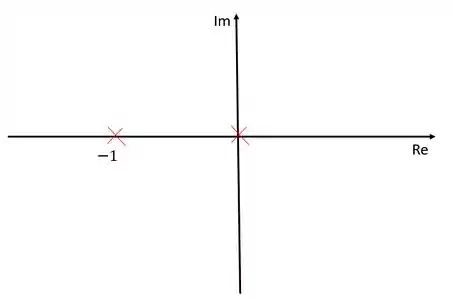
Passo 2
Nesse caso, temos dois polos a mais que zeros, o que significa que vamos ter dois zeros no infinito, e que precisaremos de duas assíntotas para nos mostrar onde esses zeros no infinito se encontram. Como é um sistema de realimentação positiva, a fórmula do ângulo da assíntota é um pouquinho diferente:
Repare que se , o ângulo é igual a , se , o ângulo será , e se r continuar aumentando, esses dois ângulos vão se repetir.
Sendo assim, teremos duas assíntotas sobre o eixo dos reais, cada uma apontando para uma direção.
Como as assíntotas estão sobre o eixo dos reais, não faz sentido calcular o ponto de interseção delas com essse eixo, concorda?
Passo 3
Agora, já temos tudo que precisamos e podemos fazer nosso esboço, olha só:
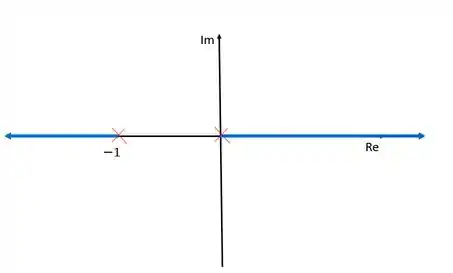
Como é um sistema de realimentação positiva, o lugar das raízes só existe se a sua esquerda houver um número par de polos e zeros. Por isso, não existe lugar das raízes entre os dois polos, uma vez que nesse intervalo só existe um polo à esquerda.
Como as assíntota indicam e , um dos ramos tede a sobre o eixo dos reais e o outro ramo tende a , também sobre o eixo dos reais.
Repare também que esse sistema é instável independente do valor de , já que não existe nenhum valor de que deixe as duas raízes negativas.
Resposta
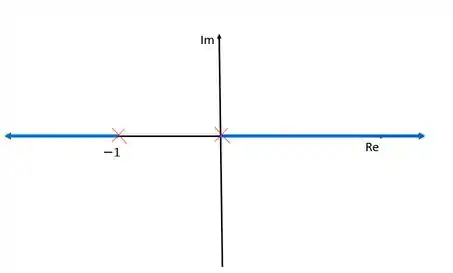
Exercício Resolvido #8
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exemplo 8.9. Adaptado
Esboce o lugar geométrico das raízes para um sistema com realimentação unitária positiva e a seguinte função de transferência em malha aberta:
Passo 1
Trata-se de um sistema com realimentação positiva. Isso quer dizer que todas as regras que usamos até aqui são válidas com exceção de duas: o lugar das raízes existe no eixo dos reais se à sua esquerda existir uma quantidade par de polos e zeros, e a soma de todos os ângulos em qualquer ponto do lugar das raízes é um múltiplo par de .
Vamos começar, como sempre, representando os nossos polos e zeros no diagrama. Nesse exercício temos dois polos: e .
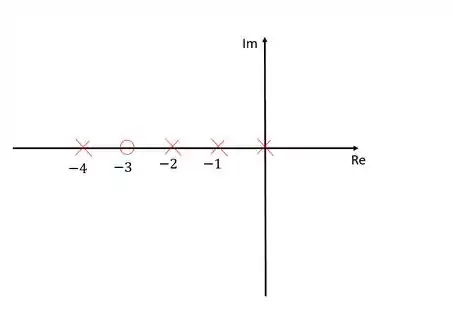
Passo 2
Nesse caso, temos três polos a mais que zeros, o que significa que vamos ter três zeros no infinito, e que precisaremos de duas assíntotas para nos mostrar onde esses zeros no infinito se encontram. Como é um sistema de realimentação positiva, a fórmula do ângulo da assíntota é um pouquinho diferente:
Repare que se , o ângulo é igual a , se , o ângulo será , se , o ângulo será e se r continuar aumentando, esses ângulos vão se repetir.
Sendo assim, teremos duas assíntotas sobre o eixo dos reais, cada uma apontando para uma direção.
Agora, vamos calular onde essas assíntotas interceptam o eixo dos reais para podermos representa-las:
Vamos representar as assíntoas agora:
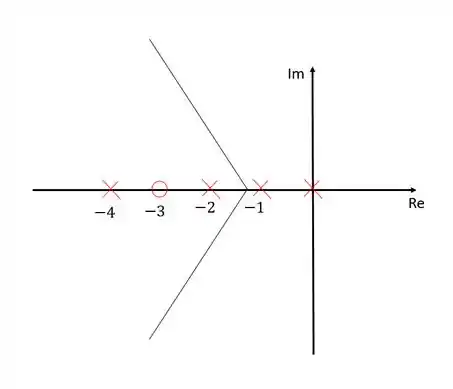
Uma assíntota tem inclinação , outra , e uma terceira tem inclinação e está sobre o eixo dos reais. Além disso essas assíntotas interceptam o eixo dos reais em .
Passo 3
Agora, já temos tudo que precisamos e podemos fazer nosso esboço, olha só:
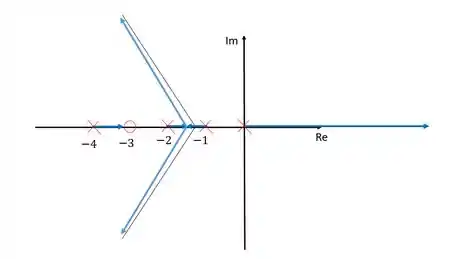
Como é um sistema de realimentação positiva, o lugar das raízes só existe se à sua direita houver um número par de polos e zeros. Além disso todas as outras regras foram satisfeitas: o número de ramos é igual ao número de polos, cada ramo nasce em um polo e morre em um zero e a simetria em relação ao eixo dos reais foi respeitada.
Nesse problema, a gente tinha três polos a mais que zero, e por isso três ramos tenderam aos zeros no infinito que são determinados pelas assíntotas.
Resposta