Substituição direta
Teoria
Introdução
No tópico anterior, nós vimos a técnica do lugar geométrico das raízes. Essa técnica nos mostrava em qual lugar do plano se encontrariam as raízes da equação característica, conforme nós variamos um parâmetro, o ganho por exemplo.
Agora nós veremos uma técnica parecida. O método da substituição direta vai ser uma ferramenta muito importante no nosso estudo do controle de processos. Esse método vai nos mostrar o limite superior do ganho da nossa malha.
Então por exemplo. Dado o seguinte sistema:
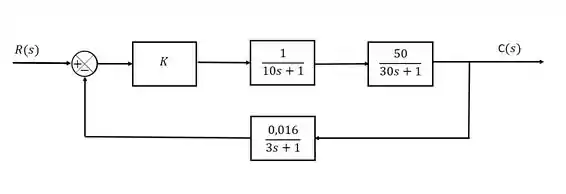
Nós vamos obter:
Que são os valores de ganho e período final, ou seja, os valores de ganho e período que fazem com que a resposta do sistema esteja no limite da estabilidade, ou em outras palavras, que o sistema seja marginalmente estável. Isso quer dizer que se aumentarmos um pouquinho que seja o ganho, o sistema já se torna instável.
O índice em e vem da palavra em inglês ultimate. E serve justamente para indicar o ganho ou período final (último).
Antes de mergulharmos de cabeça no método vamos relembrar umas coisas que nós vimos no nosso tópico de estabilidade. Vou destacar especialmente esses dois pontos:
- Para ser estável, um sistema precisa que todos os coeficientes da sua equação característica tenha o mesmo sinal. Esse é um critério necessário, porém não suficiente, o que quer dizer que caso o sistema não atenda a esse critério ele necessariamente é instável, porém, se ele atender não podemos determinar nada sobre sua estabilidade a partir desse critério;
- Para ser estável, todas as raízes da equação característica precisam necessariamente estar no semiplano complexo da esquerda, ou seja, terem a sua parte real negativa. Caso qualquer raiz da equação característica apresente parte real positiva, o sistema se torna automaticamente instável.
O método da substituição direta
Então vimos que para que um sistema seja estável, as raízes de sua equação característica precisam se encontrar todas no semiplano complexo da esquerda. Graficamente, isso quer dizer que elas precisam se encontrar na seguinte região:
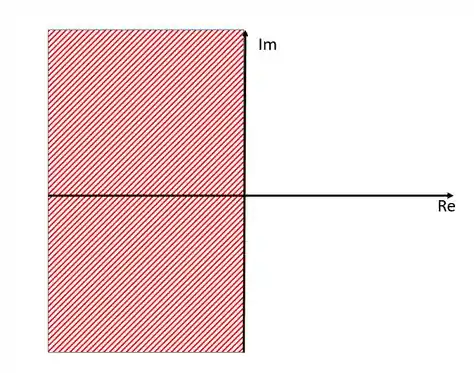
Ou seja, a raiz precisa ser um número com a parte real negativa, ou um número puramente real negativo se ele se encontrar sobre o eixo dos reais.
Pelo gráfico podemos ver que quando a raiz for um número imaginário puro (estiver sobre o eixo dos imaginários) o sistema estará no seu limite de estabilidade, ou seja, qualquer variação para a direita o tornará instável.
Então o método da substituição direta vai forçar que a raiz da equação esteja sobre o eixo dos imaginários, levando o sistema ao seu limite e encontrando os valores dos seus parâmetros que causam essa situação.
Por exemplo, uma raiz qualquer tem a seguinte fórmula geral:
Onde é a parte real, e é a parte imaginária.
Se quisermos encontrar o limite de estabilidade do nosso sistema, assumiremos que:
Ou seja, a raiz se encontra sobre o eixo dos imaginários.
Após fazer as substituições devemos separar a parte real da parte imaginária e encontrar os valores de ganho e frequência final que satisfazem ao sistema.
Com o valor de é possível encontrar através da fórmula:
Para organizar tudo na sua cabeça eu fiz um passo a passo:
- Obter a equação característica do seu sistema;
- Fazer as substituições:
- Separar a parte real da parte imaginária e igualar ambas as partes a ;
- Resolver o sistema resultante e encontrar os valores de e ;
- Encontrar o valor de período final pela fórmula:
Entendeu tudinho? Não entendeu? Acha que sim? Não faz pergunta difícil? Calma, vamos fazer um exemplo para tentar ver como tudo isso funciona na prática.
Botando a mão na massa
Vamos retomar então nosso exemplo lá do início:
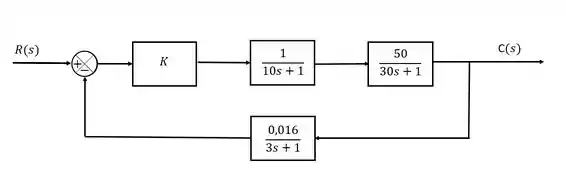
O primeiro passo é determinar nossa equação característica. Como esse é um feedback comunzão, nossa equação característica vai ficar assim:
Rearranjando:
Multiplicando os termos em parênteses:
Agora que já encontramos a nossa equação característica podemos fazer nossas substituições:
Substituindo na equação característica:
Sabendo que:
Temos:
Rearranjando:
Para que a igualdade acima seja verdadeira, tanto a parte real quanto a parte imaginário precisam ser iguais a , sendo assim:
Agora precisamos resolver esse sistema. Como a primeira equação só depende as frequência, podemos começar por ela
O resultado em que sempre será irrelevante para nós, então:
Agora, com o valor de , encontramos na segunda equação:
Aproximação de Padé
Em alguns casos, podemos encontrar processos com tempo morto.
O tempo morto é representado no domínio frequência como uma função exponencial:
Onde é o tempo morto.
Quando temos esse termo, não conseguimos resolver a nossa substituição direta normalmente porque a exponencial bagunça tudo.
Então a gente, que não é bobo nem nada, dá uma “trapaceada” e usa uma aproximação conhecida como aproximação de Padé.
Essa aproximação, some com o termo exponencial e transfora ele em um termo mais amigável que é bem mais fácil de trabalhar:
Então se nós o bloco do transmissor do nosso exemplo tivesse um tempo morto de , ele seria escrito da seguinte forma:
Quando fôssemos aplicar o método da substituição direta, não poderemos fazer com a função do jeito que está, precisaremos então aplicar a aproximação de Padé. A função de transferência ficaria então:
O método da substituição direta
Botando a mão na massa
Aproximação de Padé
Exercícios Resolvidos
Exercício Resolvido #1
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Problema 6-10. Adaptado
Um processo pode ser definido pela seguinte função de transferência:
Onde e são as constantes de tempo da válvula de controle e do transmissor, respectivamente. Considerando um controlador proporcional, encontre a faixa do ganho da malha, para a qual a malha é estável se e
Passo 1
Primeiramente devemos identificar noss malha para podermos encontrar a equação característica dela.
Como a função de transferência dada no exercício já envolve as dinâmicas da válvula e do transmissor, a malha pode ser simplificada da seguite maneira:
Onde é a função de transferência do processo, válvula e transmissor que foi dada no enunciada e é a função de transferência do controlador.
Como o enunciado diz que o controlador [e do tipo proporcional:
E como a malha é uma malha do tipo feedback, a função de transferência equivalente fica:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Com os valores das constantes dados, nossa função de transferência fica assim:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Uma vez que temos a equação característica bonitinha, o próximo passo é fazer a substituição:
Como:
Agora devemos separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Portanto:
Passo 4
O enunciado pede que a gente encontre a faixa de estabilidade pra , entretanto achamos apenas o limite superior.
Para achar o limite inferior, usamos o critério dos coeficientes, que diz que para a malha ser estável todos os coeficientes devem possuir o mesmo sinal.
Sendo assim:
Portanto, a faixa de estabilidade para o ganho da malha é:
Resposta
Exercício Resolvido #2
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Problema 6-8c. Adaptado
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Agora devemos substituir as funções de transferência do controlador e do processo na nossa equação característica:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Finalmente então, podemos aplicar a nossa substituição para encontrar o ganho e período finais:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #3
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Problema 6-8d. Adaptado
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Como estamos trabalhando com um controlador proporcional, a função de transferência para o controlador será:
E a do processo:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Fazendo aquela substituição marota:
Como:
Devemos então separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Substituindo o valor de :
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #4
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 254, Problema 6-8f. Adaptado
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Como estamos trabalhando com um controlador proporcional, a função de transferência para o controlador será:
Porém, aqui esbarramos com um problema. A função do processo tem um termo exponencial: o famoso tempo morto.
Sempre que precisarmos fazer substituição direta em uma função de transferência com tempo morto nós acionaremos o nosso megazord chamado aproximação de Padé.
Relembrando a fórmula da aproximação de Padé:
Para o nosso exercício então:
A nossa função de transferêncua para o processo será então:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Hora de aplicar nossa substituição:
Como:
Agora, já sabe né, devemos separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Da parte real:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #5
Elaboração própria
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Para o método da substituição direta, o que tilizamos é a equação característica da malha, que nada mais é que o denominador da função de gransferência queivalente, ou seja, a nossa equação característica é:
Passo 2
O nosso controlador é do tipo proporcional, portanto sua função de transferência será:
E a do processo:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Aplicando a nossa famosa substituição:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na expressão da parte real:
Substituindo o valor de :
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #6
Elaboração própria
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais sabendo que o controlador é do tipo proporcional e que:
Passo 1
Essa é aquela malha feedback mais clássica de todas, cuja função de trsnferência equivalente é a seguinte
Se você não se lembra como chegar nessa expressão, dá um revisadinha na aula de álgebra de diagrama de blocos, essa deduação tem que estar na ponta da língua.
Porém, para fazer a substituição direta precisamos mesmo é da equação característica, que é o denominador da função de transferência
Passo 2
Agora devemos substituir as funções de transferência do controlador e do processo na nossa equação característica:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Finalmente então, podemos aplicar a nossa substituição para encontrar o ganho e período finais:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #7
Elaboração própria
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais sabendo que o controlador é do tipo proporcional e que:
Passo 1
Nesse exercício temos uma malha feedback com controlador, válvula, processo e transmissor. Essa malha tem a seguinte função de transferência equivalente:
Se você não se lembra como chegar nessa expressão, dá um revisadinha na aula de álgebra de diagrama de blocos, essa deduação tem que estar na ponta da língua.
Sendo assim, nossa equação característica será:
Passo 2
Agora devemos substituir as funções de transferência do controlador e do processo na nossa equação característica:
Substituindo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Aplicando aquela substituição marota:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Multiplicando toda equação por :
Substituindo na expressão da frequência:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo:
Resposta
Exercício Resolvido #8
Elaboação própria
Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Como estamos trabalhando com um controlador proporcional, a função de transferência para o controlador será:
Só que dessa vez apareceu um termo exponencial que indica um tempo morto, ou seja temos que pedir ajuda para o nosso amigo Padé e sua aproximação:
Para o nosso exercício então:
A nossa função de transferêncua para o processo será então:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Fazendo aquela substituição esperta:
Mas:
Agora, já sabe né, devemos separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Substituindo na parte real:
Substituindo na expressão da frequência:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo: