Margem de ganho e margem de fase
Produzido por Alexandre NunesTeoria
Introdução
Agora que já aprendemos o que é resposta em frequência, já vimos como esboçar os diagramas de Bode e Nyquist e também como analisar a estabilidade de um sistema através deles, só está faltando uma coisinha para a gente fechar esse capítulo de resposta em frequência: entender o que é margem de ganho e margem de fase.
Esses dois conceitos estão diretamente relacionados ao estudo de resposta de frequência de um sistema e a sua estabilidade. Mas como assim?
Vamos continuar com o exemplo do último tópico. Nós vimos que para a função de transferência abaixo:
O diagrama de Bode resultante foi:
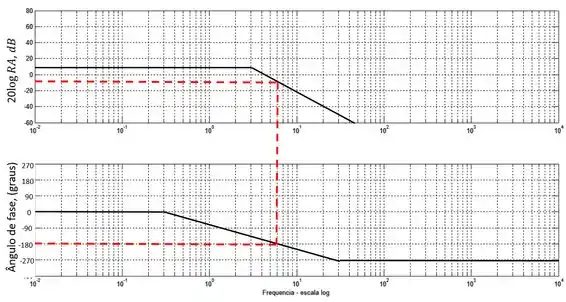
Como na frequência em que o ângulo de fase era a razão de amplitude em decibéis foi menor que , concluímos que o sistema é estável.
“Ok, se o sistema do jeito que tá ali é estável, quer dizer que eu posso aumentar um pouco o ganho dele certo?” Correto!
“Mas quanto eu posso aumentar até que ele fique instável?” É exatamente isso que os valores de margem de ganho e de fase e vão nos informar: o quanto podemos alterar uma função de transferência até que ela deixe de ser estável. Vamos aprender como obter esses valores tanto a partir do Diagrama de Bode quanto do Diagrama de Nyquist. Bora?
Definições
Antes de partirmos para a ação e ir para os diagramas, vamos entender um pouco melhor esses dois conceitos.
Margem de ganho representa o fator pelo qual o ganho total de um sistema deve aumentar para torna-lo instável. Ou seja:
Onde é o ganho final, ou seja, o valor máximo que o ganho pode ter para que o sistema não seja instável.
Dessa forma, se uma malha tem ganho total e margem de ganho , o ganho final da malha será , pois:
A margem de ganho também pode ser calculada pelo inverso da razão de amplitude de um sistema na frequência em que o ângulo de fase é . Ou seja:
Já margem de fase determina o quanto de atraso a malha ainda aguente antes de se tornar instável. Matematicamente ele é definido como a diferença entre e o ângulo de fase na frequência em que a razão de amplitude é igual a unidade. Ou seja:
O ganho de margem e ganho de fase são importantes porque muitas vezes eles servem como parâmetros de projeto e através deles é possível determinar quão bem projetado e sintonizado está o sistema.
Para que o sistema seja estável, ambas as margens devem ser positivas. Além disso, para um bom desempenho do sistema de controle é desejável que a margem de ganho esteja acima de 6 e a margem de fase esteja entre e .
Margem de ganho e fase pelo Diagrama de Bode
Uma das formas de se obter a margem de ganho e a margem de fase é através do diagrama de Bode.
A margem de ganho pode ser obtida encontrando a diferença entre a curva de razão de amplitude e a unidade na frequência em que o ângulo de fase é . Quando estivermos trabalhando com a razão de amplitude em decibéis (na maioria dos casos), devemos ver a diferença entre a razão de amplitude e a linha correspondente à razão de amplitude . O gráfico genérico abaixo mostra melhor isso.
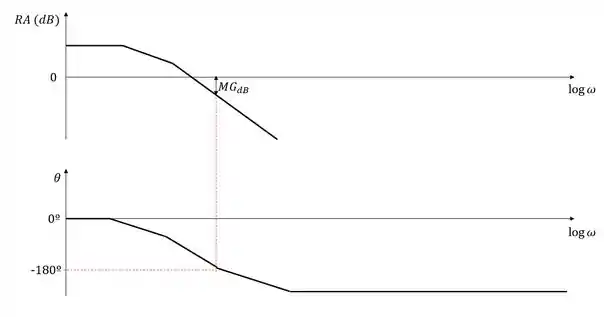
Sendo assim, para se obter a margem de ganho através do diagrama de Bode, devemos encontrar a frequência em que o ângulo de fase é e então ver a diferença da curva de razão de amplitude para a linha do zero nessa mesma frequência.
Para o caso acima, a margem de ganho é positiva e o sistema é estável. Caso na frequência em que o ângulo de fase é a curva da razão de amplitude fosse positiva, a margem de ganho seria negativa e o sistema é instável.
Além disso, quando o gráfico da razão de amplitude está em decibéis a margem de ganho também é dada em decibéis. Dessa forma, caso seja necessário fazer uma conversão, a relação entre as duas margens de ganho é a seguinte:
Para calcular a margem de fase devemos encontrar a frequência em que a razão de amplitude é (ou de o diagrama estiver em decibéis) e calcular a diferença da curva do ângulo de fase para nessa frequência. Para o mesmo gráfico genérico acima, vamos identificar a margem de fase:
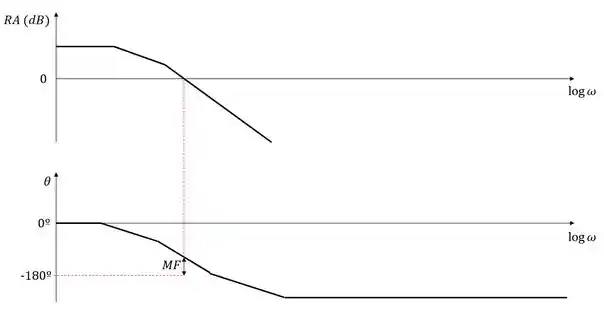
Quando a curva do ângulo de fase está acima de na frequência em que a margem de fase é positiva e o sistema é estável. Caso estivesse abaixo, a margem de fase seria negativa e o sistema seria instável.
Margem de ganho e fase pelo Diagrama de Nyquist
Agora vamos obter margem de ganho e de fase usando o Diagrama de Nyquist. Para entender como fazer isso vamos usar o diagrama hipotético abaixo:
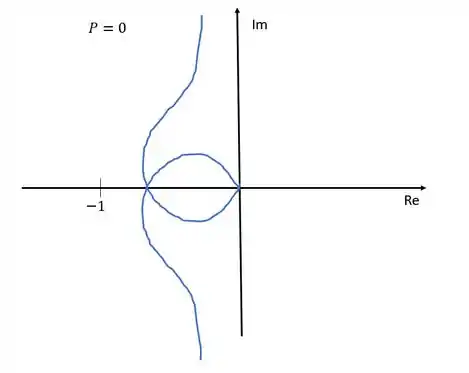
O critério de Nyquist diz que:
E para o sistema ser estável é necessário que . Como já está informado na imagem que precisamos que também seja para que o sistema seja estável. é o número de voltas em torno de . Dessa forma, enquanto o ponto em que o diagrama polar cruza o eixo dos reais estiver à direta de o sistema é estável. Se você não entendeu nada do que eu acabei de falar, seria legal dar uma revisada na aula de Critério de Nyquist.
Para achar a margem de ganho via Diagrama de Nyquist, nós precisamos da distância entre o ponto que o diagrama cruza o eixo dos reais e a origem. A margem de ganho será o inverso dessa distância.
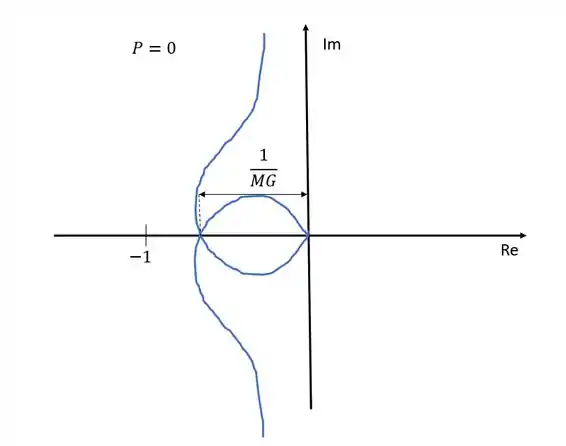
Se o ponto que o diagrama cruza o eixo dos reais fosse , por exemplo, a margem de ganho seria . O que quer dizer que o ganho total do sistema poderia ser dobrado sem ficar instável.
Para calcular a margem de fase, devemos encontrar um ponto do diagrama com módulo e calcular o ângulo dele com relação ao eixo dos reais.
Para conseguir identificar esse ponto cujo módulo é , podemos fazer um círculo com centro na origem e raio igual a . Onde esse círculo cruzar o diagrama é o ponto que precisamos.
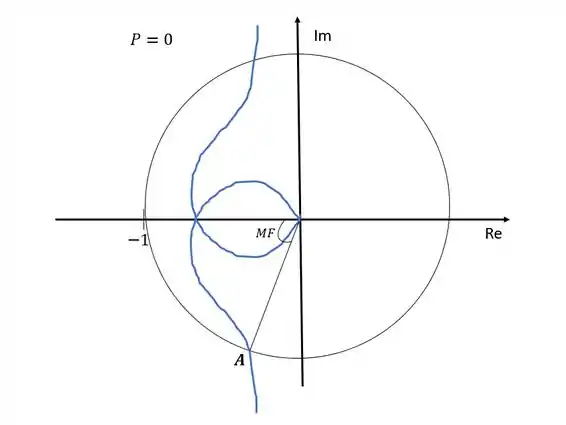
O ponto é o ponto que procuramos. Para determinar a margem de fase precisamos então da medida do ângulo entre a linha que liga esse ponto à origem e o eixo dos reais, como mostra a imagem acima.
Encontrar a margem de fase pelo Diagrama de Nyquist pode ser bem difícil e por vezes requer aproximações, o que acaba envolvendo muitas incertezas. Sendo assim, é bem mais confiável encontrar a margem de fase pelo Diagrama de Bode.
Definições
Margem de ganho e fase pelo Diagrama de Bode
Margem de ganho e fase pelo Diagrama de Nyquist
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um sistema tem ganho e margem de ganha . Qual o ganho máximo que o sitema pode operar?
Passo 1
Primeiramente vamos fazer a conversão do ganho para escala linear.
Como:
Teremos:
Portanto:
Passo 2
Pela definição, margem de ganho é o fator pelo qual o ganho pode ser aumentado antes que o sistema se torne instável.
Onde , é o ganho final.
Sendo assim:
Resposta
Exercício Resolvido #2
Transpetro 2006 – Engenheiro de automação – Questão 38
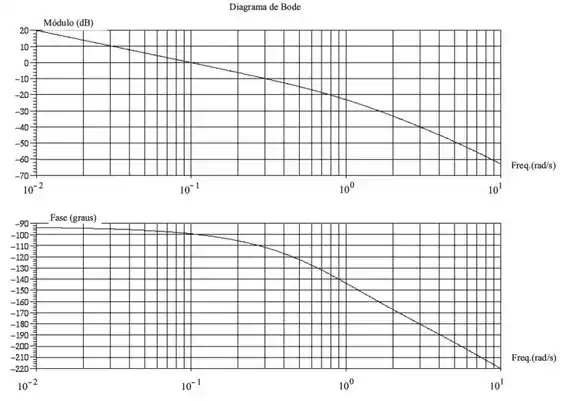
As figuras representam os diagramas de Bode para a função de transferência em malha aberta de um determinado cistema físico. A margem de ganho, em dB, e a margem de fase, em graus, valem respectivamente:
- 80 e 100
- 20 e 140
- 70 e 60
- 40 e 80
- 60 e 120
Passo 1
Primeiramente, vamos encontrar a margem de ganho.
Para isso, precisaremos encontrar a razão de amplitude na frequência em que a fase é .
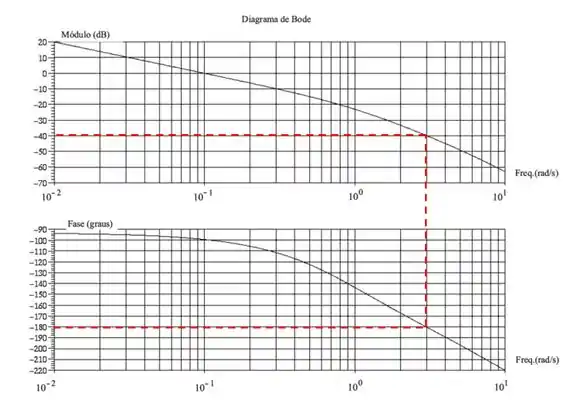
Pela imagem, podemos ver que na frequência crítica, a razão de amplitude é . A margem de ganho é:
Passo 2
Para encontrar a margem de fase, precisamos encontrar o ângulo de fase na frequência em que a razão de amplitude é .
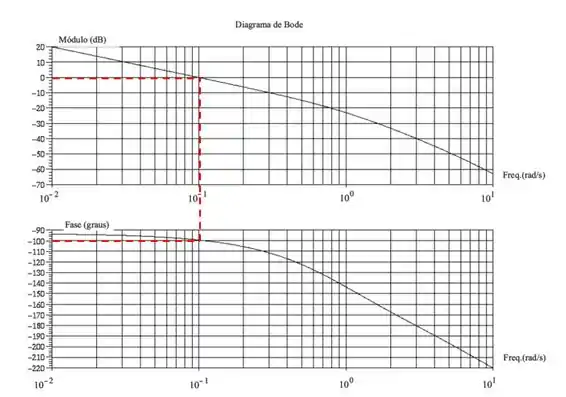
A margem de fase é calculada como a diferença entre esse ângulo de fase e . Sendo assim:
Resposta
d) 40 e 80
Exercício Resolvido #3
Elaboração própria
Dado o diagrama de Bode abaixo, encontre a margem de ganho e a margem de fase do sistema.
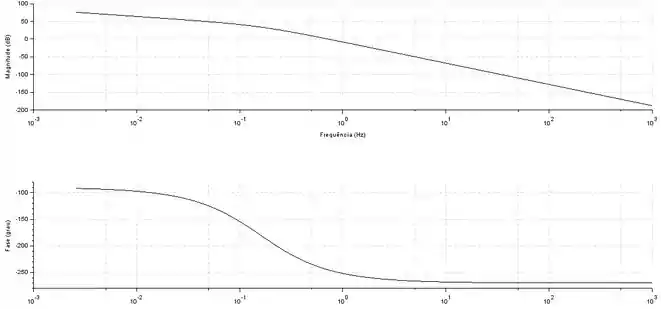
Passo 1
Primeiramente, vamos calcular a margem de ganho. A margem de ganho pode ser encontrada via diagrama de Bode através da razão de amplitude do sistema na frequência em que o ângulo de fase é . Vamos encontrar esse valor então:
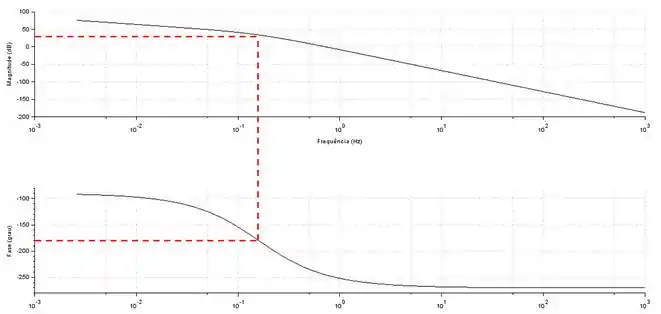
Pela figura, podemos ver que a razão de amplitude na frequência crítica é mais ou menos . A margem de ganho pode ser calculada como a diferença entre e esse valor de razão de amplitude. Sendo assim, a margem de ganho será:
Uma margem de ganho negativa indica que o sistema é instável, ou seja, tem um valor de ganho acima do ganho máximo.
Passo 2
Vamos agora calcular a margem de fase.
Para isso, precisamos encontar o valor do ângulo de fase na mesa frequência em que aa razão de amplitude é igual a .
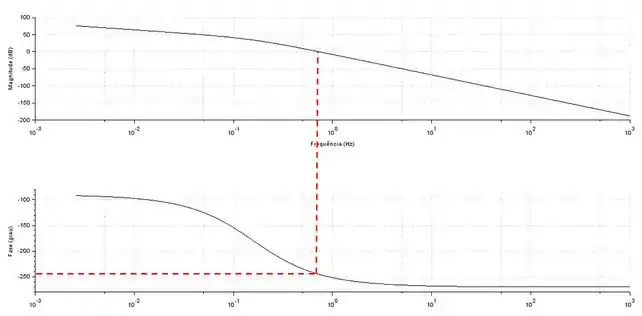
Pela figura, podemos estimar esse valor como aproximadamente .
A margem de fase é a diferença desse valor de ângulo de fase para . Sendo assim:
A margem de fase negativa indica que o sistema é instável, o que corrobora a conclusão que chegamos com a margem de ganho.
Resposta
Exercício Resolvido #4
Elaboração própria
Dado o diagrama de Bode abaixo, encontre a margem de ganho e a margem de fase do sistema.
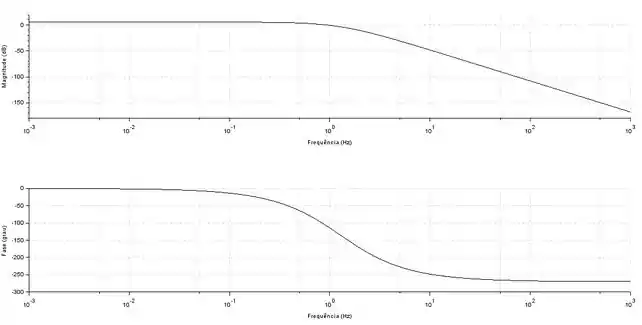
Passo 1
Vamos calcular a margem de ganho encontrando a razão de amplitude na frequência crítica.
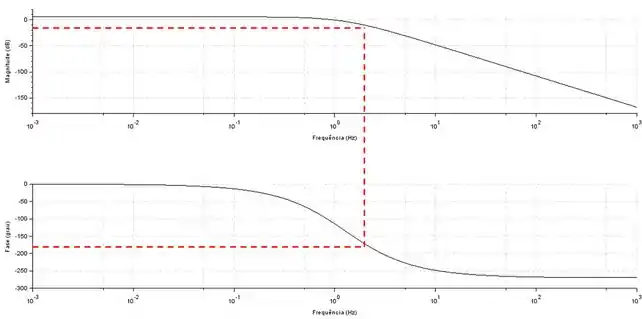
Pela figura, podemos ver que a razão de amplitude na frequência crítica é aproximadamente . A margem de ganho pode ser calculada como a diferença entre e esse valor de razão de amplitude. Sendo assim, a margem de ganho será:
Como a mergem de ganho é positiva, o sistema é estável.
Passo 2
Vamos agora calcular a margem de fase.
Para isso, precisamos encontar o valor do ângulo de fase na mesa frequência em que aa razão de amplitude é igual a .
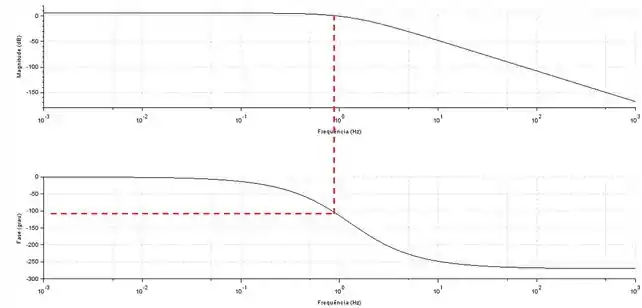
Pela figura, podemos estimar esse valor como aproximadamente .
A margem de fase é a diferença desse valor de ângulo de fase para . Sendo assim:
Lembrando que margem de fase positiva indica sistema estável.
Resposta
Exercício Resolvido #5
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 10.13. Adaptado.
Dado o diagrama de Nyquist abaixo:
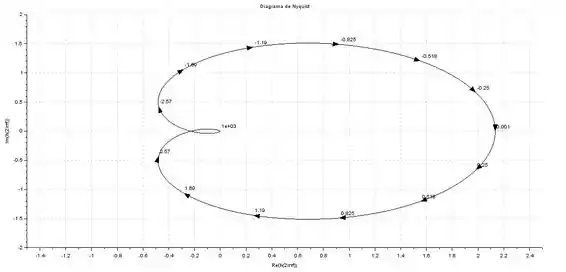
Calcule a margem de ganho e diga se o sistema é estável ou instável.
Passo 1
Para encontrar a margem de ganho, precisamos encontrar o ponto onde o diagrama de Nyquist cruza o eixo dos reais:
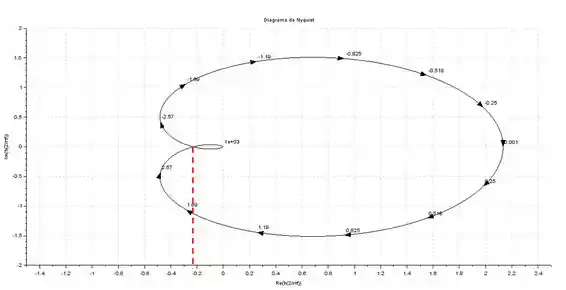
Esse ponto é aproximadamente .
Passo 2
Para encontrar a margem de ganho, precisamos apenas dividir por esse valor:
Como a margem de ganho resultou em um número maior que , o sistema é estável.
Se estivéssemos trabalhando com margem de ganho em decibéis, para o sistema ser estável, a margem de ganha precisaria ser maior que .
Resposta
Sistema estável.
Exercício Resolvido #6
Elaboração própria
Dado o diagrama de Nyquist abaixo:
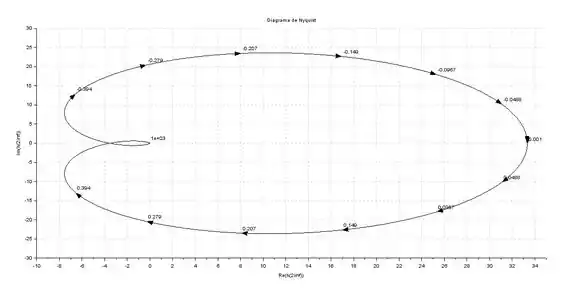
Calcule a margem de ganho e diga se o sistema é estável ou instável.
Passo 1
Para encontrar a margem de ganho, precisamos encontrar o ponto onde o diagrama de Nyquist cruza o eixo dos reais:
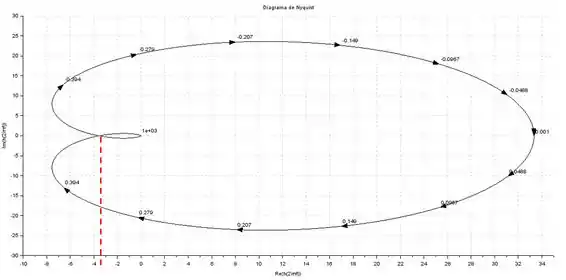
Esse ponto é aproximadamente .
Passo 2
Para encontrar a margem de ganho, precisamos apenas dividir esse valor por :
Como a margem de ganho resultou em um número menor que , o sistema é instável.
Se estivéssemos trabalhando com margem de ganho em decibéis, para o sistema ser estável, a margem de ganha precisaria ser maior que .
Resposta
Sistema instável.
Exercício Resolvido #7
Elaboração própria
Dado o diagrama de Nyquist abaixo:
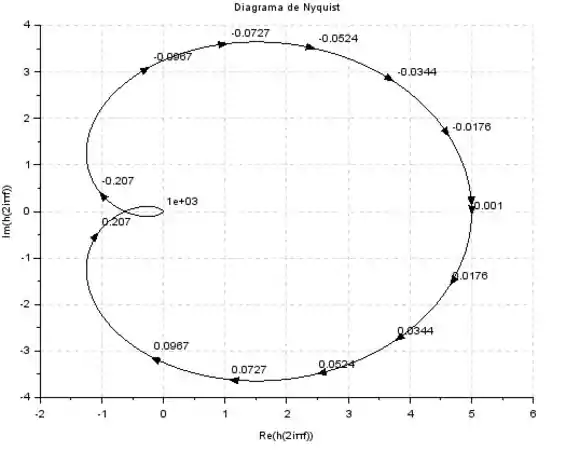
Calcule a margem de fase e diga se o sistema é estável ou instável.
Passo 1
Para calcular a margem de fase, precisamos traçar um segmento de magnitude e girá-lo para que a gente consiga encontrar um ponto do diagrama de Nyquist com módulo exatamente igual a .
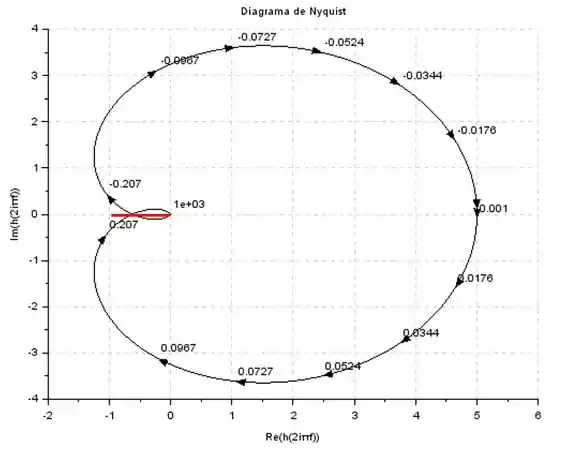
Passo 2
Agora, devemos girar esse segmento até encontrar a linha do diagrama de Nyquist:
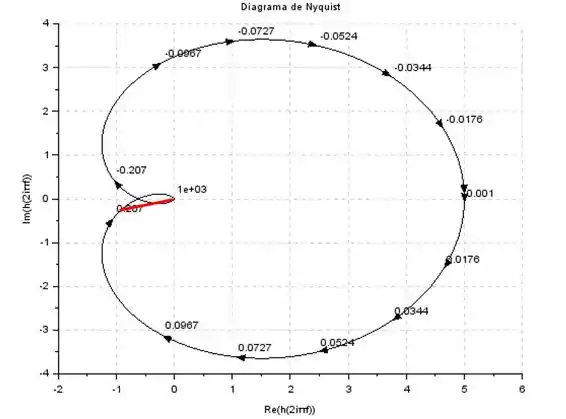
Passo 3
Para calcular a margem de fase, devemos calcular o ângulo que esse exato ponto do diagrama de Nyquist faz com o eixo real. Se tentarmos fazer uma aproximação no olhômetro mesmo, podemos chutar que esse ponto está em .
Sendo asism, a margem de fase será:
Resposta
Exercício Resolvido #8
Norman N. Nise, Engenharia de sistemas de controle, 6ª ed., Rio de Janeiro, 2012, Exercício 10.13. Adaptado.
Obtenha a margem de ganho, margem de fase, a frequência de e a frequência de para um sistema com realimentação unitária e função de transferência em malha aberta:
Passo 1
Para encontrar tudo isso que o exercício pediu, precisamos de um diagrama de Bode. Como ele não deu o diagrama de mão beijada pra gente mas deu a função de transferência em malha aberta. Vamos nós mesmo fazer o esboço do diagrama de Bode usando a aproximação assintótica.
O primeiro passo será reescrever a função de transferência deixando todos os zeros e polos (nesse caso só polos, pois não há zeros) no formato . Portanto:
Passo 2
Vamos começar o nosso esboço representando. cada um dos termos como uma linha no diagrama de Bode:
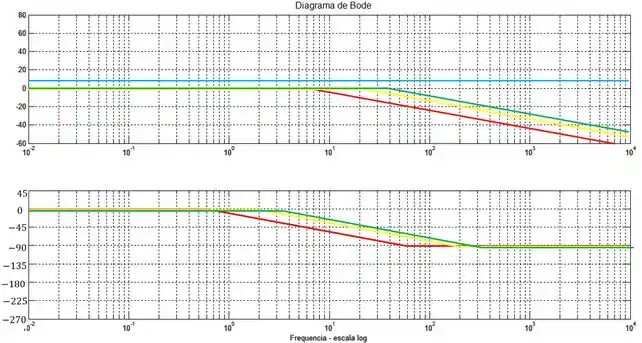
A linha azul representa a constante e as linhas vermelha, amarela e verde representam os polos com frequência de quebra em , e respectivamente
Se você não lembra as regras para traçar um esboço do diagrama de Bode através da aproximação por assíntotas, seria bacana dar uma revisadinha na aula de Diagrama de Bode.
Passo 3
Somando todas as assíntotas, teremos:
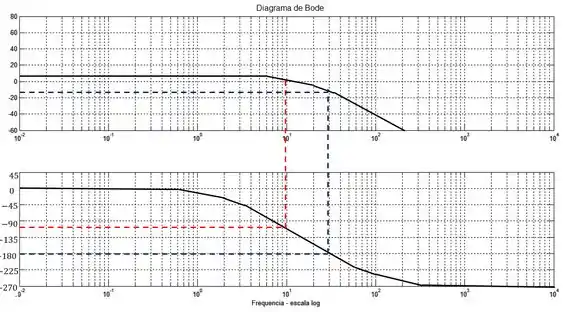
Primeiramente vamos ver a margem de ganho.
A margem de ganho é a diferença da linha do na razão de amplitude para o valor da razão de amplitude na frequeência onde o ângulo de fase é .
Pela figura (linha pontilhada azul), podemos ver que a frequência em que o ângulo de fase é é aproximadamente .
Nessa frequência a razão de amplitude é aproximadamente . Portanto:
Passo 4
Para achar a margem de fase, precisamos analisar o ângulo de fase na frequência de (linha pontilhada vermelha).
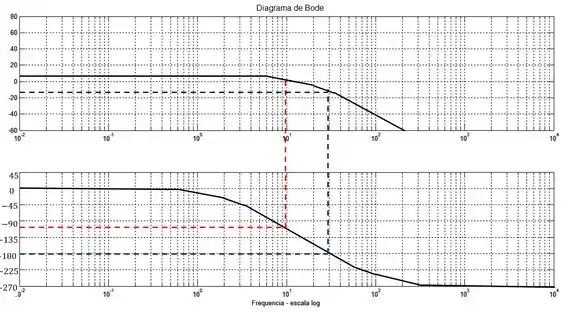
Sendo assim, a frequência de é aproximadamente .
Nessa frequência o ângulo de fase é aproximadamente . Portanto, a margem de fase será:
Lembrando que todos os valores que encontramos aqui são aproximados, uma vez que o diagrama de bode que a gente construí também é um diagrama aproximado. Além disso, pode acontecer erros de leitura na hora de determinar esses valores.