Método de Cohen-Coon e IAE
Teoria
Cohen-Coon
O método de Cohen-Coon se assemelha muito com o método de Ziegler-Nichols de malha aberta. Na verdade, o procedimento é basicamente o mesmo, o que muda é que o método de Cohen-Coon é muito melhor que o método de Zielger-Nichols quando o tempo morto do processo é muito grande.
Assim como no método de Zielger-Nichols de malha aberta, a primeira coisa que devemos fazer é analisar o gráfico do processo em malha aberta para uma entrada degrau:
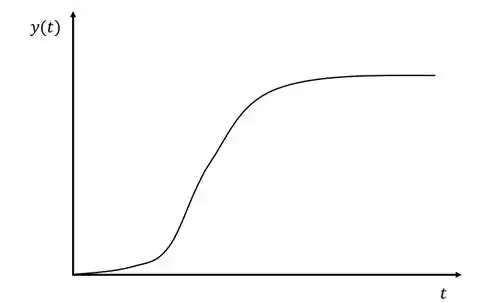
Em seguida, devemos tentar aproximar o gráfico do processo para uma função de primeira ordem com tempo morto:
Para fazer essa aproximação, devemos traçar a tangente com maior inclinação na curva de reação do processo, e determinar as constantes , e conforme a imagem abaixo:
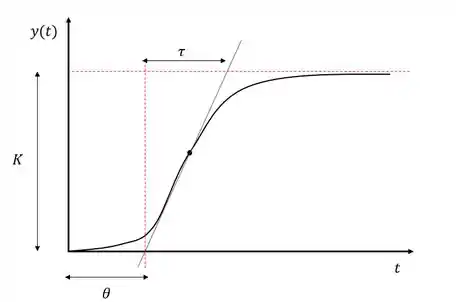
Após determinar as constantes, devemos checar se o método de Cohen-Coon poderá ser aplicado.
Esse método apresenta resultados razoáveis para a seguinte faixa:
Se a razão não estiver dentro da faixa acima, pode esquecer, o método não vai apresentar resultados bons.
Além disso, para o método não apresenta uma boa robustez, o que significa que a sintonia não é feita da melhor maneira Para sistemas com o método funciona mas não é o mais recomendado.
Sendo assim, após analisar o gráfico da curva de reação, traçar a tangente com maior assíntota, determinar , e e checar se o processo tem tempo morto alto o suficiente para usar o método de Cohen-Coon basta usar as correlações da tabela e ser feliz.
Essas correlações foram determinadas empiricamente e assim como as correlações de Ziegler-Nichols, têm como objetivo uma sintonia com decaimento , isto é, cada pico da resposta em malha fechada tem amplitude do pico anterior.
Lembrando mais uma vez que essas correlações só são úteis para os processos com na faixa adequada.
Método IAE
Um último método que veremos para sintonização de um controlador é o método da sintonização mínima integral, também chamado de IAE.
Esse método foi elaborado empiricamente com o objetivo de se reduzir o erro do processo com relação ao valor do estado estacionário para todos os pontos do processo.
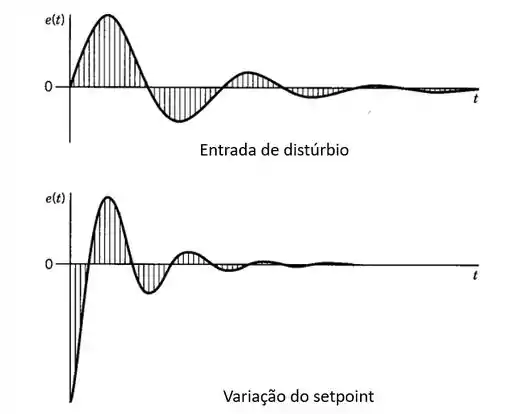
Sendo assim, o principal objetivo desse método é encontrar os parâmetros do controlador (ganho, constante de tempo integral e constante de tempo derivativa) que reduzem ao máximo o valor da integral do erro quando há a entrada de um distúrbio ou uma variação no setpoint.
Método IAE
O método da integral mínima do erro, assim como os métodos de Ziegler-Nichols de malha aberta e de Cohen-Coon utiliza-se dos valores de parâmetros do modelo aproximado de primeira ordem mais tempo morto (FOPDT) para chegar às correlações necessárias para calcular as constantes do controlador.
Isso quer dizer que, dado um processo cuja função de transferência é desconhecida, aplica-se um degrau em um distúrbio ou em um ponto fixo e mede-se o comportamento da resposta no tempo. Com o gráfico resposta versus tempo, estima-se uma função de transferência de primeira ordem com tempo morto (FOPDT) para o processo da mesma forma que fazemos para o método de Ziegler-Nichols em malha aberta e o método Cohen-Coon.
Uma vez que obtivemos os parâmetros para o modelo FOPDT, a sintonização do controlador é feita conforme as tabelas abaixo:
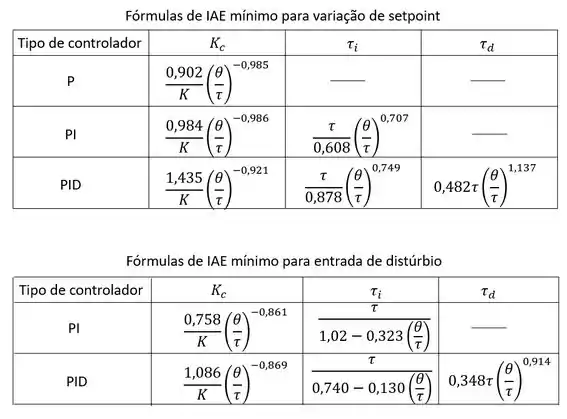
Para saber qual das duas tabelas usar, deve-se considerar o que é mais importante e que atinge o processo com mais frequência. Se o seu processo apresenta distúrbios que impactam a resposta com muita frequência o melhor é escolher a fórmula de IAE mínimo para a entrada de distúrbios. Entretanto, se o seu processo muda o setpoint constantemente, as melhores correlações serão aquelas para variação de setpoint.
As fórmulas para entrada de distúrbio e um controlador do tipo proporcional foram omitidas porque os desenvolvedores do método consideraram que esse tipo de controlador não é adequado para reduzir o erro causado por um distúrbio.
Além disso, deve-se ter em mente que o método é válido apenas para processos que se enquadram na seguinte faixa:
Método IAE
Método IAE
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Para o sistema representado pela curva de reação ao degrau abaixo, defina qual o melhor método de sintonização a ser usado: Cohen-Coon e método de integral mínima do erro (IAE).
Passo 1
Para saber qual o melhor método para usar, devemos aproximar o processo a uma função de transferência de primeira ordem com tempo morto (FOPDT), conforme o modelo abaixo:
Para isso, devemos conseguir os parâmetros , e da imagem utilizando o método ma máxima tangente. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
Passo 2
Vamos aplicar o método no nosso processo então:
Dessa forma, podemos estimar nossas constantes como:
E a função FOPDT ficará:
Passo 3
Para decidir qual o melhor método para usar, devemos olhar para a relação entre o atraso (tempo morto) e a constante de tempo.
O método de Cohen-Coon é ótimo para processos com com grandes atrasos. Geralmente se utiliza a faixa:
Já o método de integral mínima do erro IAE, funciona melhor com processos com tempo de atraso baixos e mais lentos (altos valores de ). A faixa mais adequada é:
Para o nosso processo, a relação entre essas duas constantes é:
Logo, a melhor opção é o método de IAE.
Resposta
Método de IAE.
Exercício Resolvido #2
Elaboração própria
Para o sistema representado pela curva de reação ao degrau abaixo, defina qual o melhor método de sintonização a ser usado: Cohen-Coon e método de integral mínima do erro (IAE).
Passo 1
Para saber qual o melhor método para usar, devemos aproximar o processo a uma função de transferência de primeira ordem com tempo morto (FOPDT), conforme o modelo abaixo:
Para isso, devemos conseguir os parâmetros , e da imagem utilizando o método ma máxima tangente. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
Passo 2
Vamos aplicar o método no nosso processo então:
Dessa forma, podemos estimar nossas constantes como:
E a função FOPDT ficará:
Passo 3
Para decidir qual o melhor método para usar, devemos olhar para a relação entre o atraso (tempo morto) e a constante de tempo.
O método de Cohen-Coon é ótimo para processos com com grandes atrasos. Geralmente se utiliza a faixa:
Já o método de integral mínima do erro IAE, funciona melhor com processos com tempo de atraso baixos e mais lentos (altos valores de ). A faixa mais adequada é:
Para o nosso processo, a relação entre essas duas constantes é:
Logo, a melhor opção é o método de Cohen-Coon.
Resposta
Método de Cohen-Coon.
Exercício Resolvido #3
Elaboração própria
Para o sistema representado pela curva de reação ao degrau abaixo, utiliza o método de Cohen-Coon para sintonizar um controlador PI.
Passo 1
Para aplicar o método de Cohen-Coon, devemos aproximar o processo a uma função de transferência de primeira ordem com tempo morto (FOPDT), conforme o modelo abaixo:
Para isso, devemos conseguir os parâmetros , e da imagem utilizando o método ma máxima tangente. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
Passo 2
Vamos aplicar o método no nosso processo então:
Com esse esboço, podemos estimar nossas constantes como:
E a função FOPDT ficará:
Antes de fazer a sintonização, vamos checar se o processo pode ser sintonizado pelo método de Cohen-Coon.
O método de Cohen- Coon é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado por Cohen-Coon
Passo 3
Agora só nos resta aplicar as correlações propostas por Cohen-Coon que estão na tabela abaixo:
Como queremos um controlador PI, vamos utilizar as fórmulas da segunda linha:
Portanto, o nosso controlador terá função de transferência:
Resposta
Exercício Resolvido #4
Elaboração própria
Para o sistema representado pela curva de reação ao degrau abaixo, utiliza o método de Cohen-Coon para sintonizar um controlador PID.
Passo 1
Para aplicar o método de Cohen-Coon, devemos aproximar o processo a uma função de transferência de primeira ordem com tempo morto (FOPDT), conforme o modelo abaixo:
Para isso, devemos conseguir os parâmetros , e da imagem utilizando o método ma máxima tangente. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
Passo 2
Vamos fazer os traços para encontarar esse parâmetros no nosso processo
Agora a gente já pode estimar as nossas constantes para conseguir fazer a sintonização:
E a função FOPDT ficará:
Mas antes da gente botar a mão na massa, precisamos conferir se realmente pe uma boa ideia usar Cohen-Coon para sintonizar nosso PID
O método de Cohen- Coon é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado por Cohen-Coon
Passo 3
Agora só nos resta aplicar as correlações propostas por Cohen-Coon que estão na tabela abaixo:
Como queremos um controlador PID, vamos utilizar as fórmulas da última linha da tabela:
Portanto, o nosso controlador PID ficará com a seguinte FT:
Resposta
Exercício Resolvido #5
Elaboração própria
Considere a curva de reação a uma perturbação degrau unitário mostrada abaixo. 
Para esse processo, sintonize um controlador P, PI e PID utilizando as correlações de Cohen-Coon.
Passo 1
Primeiramente, vamso tentar achar a função de primeira ordem com tempo morto aproximada que melhor descreve o processo da figura. Essa função, terá o seguinte formato:
Então precisamos determinar os parâmetros , e através do gráfico da curva de reação. A forma de se obter esses valores está mostrada no exemplo genérico abaixo:
Passo 2
Para facilitar a nossa visualização, vamos fazer alguns traços para ficar mais fácis de enxergar os pontos que precisamos.
Agora a gente já pode estimar as nossas constantes para conseguir fazer a sintonização:
E a função FOPDT ficará:
Antes de sintonizar os três controladores, precisamos primeiro verificar se realmente o método de Cohen-Coon é apropriado para o sistema do exercício.
O método de Cohen- Coon é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado por Cohen-Coon
Passo 3
Agora só nos resta aplicar as correlações propostas por Cohen-Coon que estão na tabela abaixo:
Primeiramente, vamos fazer a sintoniza para um controlador puramente proporcional:
Pela tabela:
Portanto, o controlador P terá função de transferência:
Passo 4
Para sintonizar um controlador PI, usaremos as fórmulas da segunda linha da tabela. O controlador PI tem a seguinte função de transferência padrão:
Aplicando as correlações de Cohen-Coon:
Sendo assim, teremos a seguinte FT para um controlador PI:
Passo 5
Por fim, vamos sintonizar um controlador PID para o processo:
Usando as correlações da última linha da tabela:
Portanto, o nosso controlador PID ficará com a seguinte FT:
Resposta
Controlador P:
Controlador PI:
Controlador PID:
Exercício Resolvido #6
Elaboração própria
Um engenheiro de controle precisa sintonizar um controlador PI para um determinado processo. Esse engenheiro sabe que é bem mais comum que haja mudanças no setpoint do que no distúrbio para esse processo em específico.
Sabendo disso, o engenheiro decidiu realizar o teste da perturbação degrau unitário no sistema e registrou o comportamento da resposta no gráfico abaixo:
Sintonize o controlador para o processo usando o método de Integral Mínima do Erro (IAE)
Passo 1
O método de IAE utiliza os parâmetros da função FOPDT do sistema. Sendo assim, precisamos encontrar os parâmetros que definirão essa função para o nosso sistema conforme o modelo abaixo.
Como foi nos dados a curva de reação do sistema, nós podemos definir os parâmetros da função FOPDT como mostrado no exemplo abaixo:
Passo 2
Vamos então tentar extrair essas informações do nosso gráfico:
Pelo gráfico, podemos assumir que:
A função FOPDT que aproxima o processo será:
Antes de fazer a sintonização, vamos checar se o sistema se encontra na faixa que método exige.
O método IAE é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado pelo método IAE.
Passo 3
Já podemos então partir para a sintonização. Como o processo apresenta muito mais variações no sepoint do que no distúrbio, vamos usar a tabela para IAE mínimo para variações no setpoint.
Como queremos um controlador PI, precisaremos projetar um controlador com a seguinte função de transferência:
Pela tabela:
Portanto, o controlador PI terá função de transferência:
Resposta
Exercício Resolvido #7
Elaboração própria
Para a curva de reação ao degrau unitário abaixo, sintonize um controlador PID utilizando o método de Integral mínima do erro para perturbações no distúrbio:
Passo 1
O primeiro passo, será definir os parâmetros da função FOPDT que melhor aproxima o sistema:
Como foi nos dados a curva de reação do sistema, nós podemos definir os parâmetros da função FOPDT como mostrado no exemplo abaixo:
Passo 2
Vamos então encontrar os três parâmetros que precisamos:
Pelo gráfico, podemos assumir que:
A função FOPDT que aproxima o processo será:
Vamos agora, conferir se os parâmetros estão dentro da faixa que precisamos.
O método IAE é indicado para a seguinte faixa:
Para o nosso processo temos:
Logo, está dentro da faixa, e pode ser sintonizado pelo método IAE.
Passo 3
Vamos então aplicar as correlações do método IAE para perturbações no distúrbio.
Como queremos um controlador PID, vamos usar a última linha da tabela:
Portanto:
Resposta
Exercício Resolvido #8
Elaboração própria
Dada a curva de reação para um distpurbio degrau no setpoint mostrada abaixo, sintonize um controlador PID pelo método de Cohen-Coon e pelo método de IAE mínimo.
Passo 1
O primeiro passo, será definir os parâmetros da função FOPDT que melhor aproxima o sistema:
Como foi nos dados a curva de reação do sistema, nós podemos definir os parâmetros da função FOPDT como mostrado no exemplo abaixo:
Passo 2
Vamos então encontrar as nossas três constantes:
O ganho, , é a variação total da resposta, nesse caso, teremos:
O tempo morto, ou atraso, , é o ponto onde a tangente com maior inclinação cruza o valor da resposta inicia, pelo gráfico podemos ver que:
E a constantate de tempo, , é a diferença entre o ponto que a tangente de maior inclinação cruza o valor final e o ponto em que ela cruza o valor inicial, nesse caso:
A função FOPDT que aproxima o processo será:
Vamos agora, conferir se os parâmetros estão dentro da faixa que precisamos.
O método de Cohen-Coon é indicado para processos com atraso considerável, mais precisamente, a faixa inidaca é:
Já o método IAE é indicado para a seguinte faixa:
Para o nosso processo temos:
Portanto, atende às especificações de ambos os métodos. Vamos então fazer as sintonizações.
Passo 3
Primeiramente, vamos fazer para o método de Cohen-Coon utilizando as correlações da tabela abaixo:
Como queremos um PID, usaremos as correlações da terceira linha.
E a função de transferência do controlador será:
Passo 4
Vamos agora aplicar as correlações do método IAE para perturbações no setpoint.
Como queremos um controlador PID, vamos usar a última linha da tabela:
Portanto:
Resposta
Para o método de Cohen-Coon:
Para o método de IAE mínimo: