Síntese de controladores
Teoria
Introdução
Já vimos até aqui alguns métodos para sintonizar controladores. Esses métodos geralmente usavam alguma característica do nosso processo/planta para chegar até uma função de transferência para um controlador que fosse a melhor possível. Cada método tinha a sua própria forma de encontrar essa função de transferência, e nem sempre o que era o “melhor” para um método era também para o outro.
Continuando um pouco nessa loucura de sintonizar controladores, vamos aprender agora um outro método que tem uma abordagem um pouco diferente dos demais que vimos até agora, a síntese de controladores. A síntese de controladores tenta fazer o caminho inverso para conseguir encontrar a função de transferência do controlador. Mas como assim?
Bom, o que vai acontecer é que a gente vai especificar o tipo de resposta que a gente quer, e então a partir dessa reposta e da função de transferência da nossa planta, faremos o caminho inverso para encontrar a função de transferência do controlador.
Vamos então parar de falar e botar a mão na massa.
Fórmula da síntese
Para aplicar a síntese de controladores, precisamos encontrar uma fórmula para ela. Para isso, vamos olhar para o diagrama de blocos simplificado abaixo:
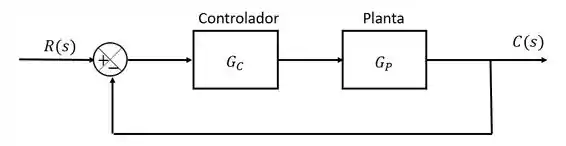
A função de transferência desse sistema será:
Sendo assim, precisamos encontrar uma expressão para a função de transferência do controlador a partir da função de transferência em malha fechada:
Reorganizando:
Então, saindo da expressão da função de transferência em malha fechada, encontramos uma fórmula para o controlador que depende da função de transferência da planta, , e também da resposta do sistema, .
Especificação da resposta
Lá em cima eu disse, que a gente ia conseguir calcular o nosso controlador fixando uma resposta, e é isso que faremos a partir de agora.
O tipo de resposta mais fácil de ser atingido e também o mais comum é a resposta em primeira ordem sem tempo morto.
Por ser a mais usada, vamos trabalhar aqui apenas com esse tipo de resposta. Entretanto, o procedimento para outras respostas é basicamente o mesmo que faremos daqui para frente, porém com cálculos mais complicados.
Vamos substituir a resposta que queremos na nossa expressão do controlador:
Manipulando um pouco esse capetinha:
Essa é a fórmula que iremos usar para encontrar os parâmetros do controlador. Repare que a única coisa que precisamos, o único parâmetro de sintonização, é a constante de tempo da resposta. Tendo esse valor e a função de transferência da nossa planta, conseguiremos encontrar facilmente a função de transferência do controlador
Encontrando a função de transferência do controlador
Para encontrar a função de transferência do controlador, precisaremos analisar a função de transferência da planta do nosso sistema, já que como vimos acima, uma coisa está diretamente relacionada a outra.
Por exemplo, vamos considerar que a nossa planta/processo tem uma função de transferência de primeira ordem, assim como a resposta que especificamos:
Substituindo na expressão do controlador:
Se manipularmos um pouco essa expressão, teremos:
Olha só! Essa expressão é muito parecida com a do controlador PI:
Portanto, por comparação, conseguimos encontrar os parâmetros do controlador:
Só lembrando para não confundir, é a constante do tempo da resposta de primeira ordem sem tempo morto desejada, , é a constante de tempo da função de transferência da nossa planta, , e é a constante de tempo integral do controlador PI.
Uma outra coisa importante de ter em mente é que quando utilizamos a síntese de controladores, não somos nós que determinamos o tipo de controlador que usaremos, e sim a função de transferência da planta do sistema, . No exemplo anterior vimos que quando essa função de transferência era de primeira ordem e sem atraso, a função de transferência do controlador naturalmente convergiu a uma forma equiparável ao do controlador PI.
Sendo assim, para saber qual será o controlador usado, devemos substituir o e ver o “formado” da expressão que encontraremos.
Nos exercícios veremos outros exemplos de que não sejam funções de transferência de primeira ordem e veremos quais controladores serão usados para cada tipo de .
Especificação da resposta
Encontrando a função de transferência do controlador
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Encontre as fórmulas de sintonização para um controlador usando o método de síntese direta para um processo de resposta instantânea:
A resposta do sistema desejada é a resposta de primeira ordem sem tempo morto.
Passo 1
A função de transferência para o sistema do enunciado é:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Onde é a constante de tempo da resposta:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Como o nosso processo é de reposta imediata (ordem 0), ele não apresenta nenhuma constante de tempo, e sua função de transferência é apena um ganho:
Substituindo na fórmula do controlador, teremos:
Essa fórmula se assemelha à fórmula de um controlador puramente integral:
Os controladores puramente integrais são indicados para processos extremamente rápidos, que é o nosso caso aqui, já que o processo do nosso exercício é de resposta imediata.
Passo 3
Por fim, precisamos apenas comparar as duas expressões e encontrar as fórmulas para os parâmetros do controlador.
Como o controlador que encontramos é puramente integral, teremos apenas um parâmetro para sintonizar, .
Pela comparação, podemos definir que:
Resposta
Exercício Resolvido #2
Elaboração própria
Sintonize um controlador PI para o processo abaixo:
Utilize a resposta de primeira ordem sem tempo morto e um valor de
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Manipulando a expressão acima para ficar parecida com um controlador PI:
A expressão genérica do controlador PI é:
Por comparação, podemos inferir que:
Substituindo :
Portanto:
Resposta
Exercício Resolvido #3
Smith & Corripio, Princípios e Prática do Controle Automático de Processos, 3ª ed. Rio de Janeiro: LTC, 2012, pag 89, Problema 7-6. Adapatado
Para a malha de controle abaixo, obtenha as fórmulas de sintonização para um PID real utilizando o método de síntese direta. Considere:
A resposta do sistema desejada é a resposta de primeira ordem sem tempo morto.
Passo 1
A função de transferência para o sistema do enunciado é:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Onde é a constante de tempo da resposta:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
A função de transferência do processo, dada no enunciado foi a seguinte:
Substituindo na fórmula do controlador, teremos:
Rearranjando um pouco:
Podemos comparar essa fórmula com a fórmula de um PID em série:
O controlador PID em série, diferentemente do PID convencional, apresenta os blocos proporcional, integral e derivativo em série, fazendo com que essas parecelas se multipliquem na função de transferência ao invés de se somar.
Passo 3
Por fim, precisamos apenas comparar as duas expressões e encontrar as fórmulas para os parâmetros do controlador.
Como o controladore encontrado é um PID, precisamos definir os três parâmetros desse controlador, , e . Por comparação, podemos encontrar as correalações:
Resposta
Exercício Resolvido #4
Lista de revisão de síntese de controladores, 2019.2, Professor Lizandro de Sousa, UFF, Questão 1
Considere que um sistema representado pela seguinte função de transferência função de transferência
Representa o processo dinâmico do processo + válvula + transmissor. Projete um controlador que resulte em uma função de transferência em malha fechada com resposta de primeira ordem:
onde é a constante de tempo em malha fechada. Compare o comportamento (em termos de velocidade) do controlador para e .
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Manipulando a expressão acima para ficar parecida com um controlador PI:
A expressão genérica do controlador PI é:
Por comparação, podemos inferir que:
Passo 3
Através dessa conclusão, podemos ver que o parâmetro afeta apenas o valor do ganho do controlador.
Para :
Para :
Isso mostra que um valor grande de ganho, , produz um constante de tempo da resposta menor, fazendo com que a resposta fique mais rápida.
Resposta
Para (mais rápido):
Para :
Exercício Resolvido #5
Lista de revisão de síntese de controladores, 2019.2, Professor Lizandro de Sousa, UFF, Questão 2
Projete um controlador para o seguinte sistema de segunda ordem (teórico):
Use o método de síntese direta que resulte em uma função de transferência em malha fechada com resposta de primeira ordem:
onde é a constante de tempo em malha fechada. Compare o comportamento do controlador para e .
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Vamos rearranjar a expressão encontrada:
Uma dica: quando tiver um processo de segunda ordem, a constante de tempo que a gente coloca em evidência é sempre a maior entre as duas, nesse caso, o .
Essa expressão pode ser comparada à expressão do PID em série que é dada abaixo:
Por comparação, podemos definir:
Passo 3
Através da comparação, podemos ver que o parâmetro afeta apenas o valor do ganho do controlador.
Para :
Para :
Logo, quanto maior o valor do ganho, menor será a constante de tempo da resposta e consequentemente mais rápido será a resposta do sistema.
Resposta
Para (mais rápido):
Para :
Exercício Resolvido #6
Lista de revisão de síntese de controladores, 2019.2, Professor Lizandro de Sousa, UFF, Questão 5. Adaptado
Um processo tem a seguinte função de transferência em malha aberta:
Use o método de síntese direta que resulte em uma função de transferência em malha fechada com resposta de primeira ordem:
E configure um PID com valor de e .
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Vamos rearranjar a expressão encontrada:
Essa expressão pode ser comparada à expressão do PID em série que é dada abaixo:
Por comparação, podemos definir:
Passo 3
Substituindo os valores dado pelo enunciado, chegaremos à seguinte expressão:
Logo:
Resposta
Exercício Resolvido #7
Lista de revisão de síntese de controladores, 2019.2, Professor Lizandro de Sousa, UFF, Questão 3
Sintetize um controlador PID paralelo a partir de um modelo do processo de segunda ordem,
sendo que a resposta desejada é de primeira ordem em malha fechada:
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem sem tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Precisamos deixar a expressão acima parecida com a de um PID em paralelo:
Colocando em evidência:
Mudando a ordem dos termos entra parênteses:
Passo 3
Agora, já podemos comparar a expressão para o controlador que encontramos com a expressão geral do PID em paralelo:
Portanto, as fórmulas de sintonização serão as seguintes:
Resposta
Exercício Resolvido #8
Lista de revisão de síntese de controladores, 2019.2, Professor Lizandro de Sousa, UFF, Questão 4. Adaptado
Configure um controlador PI que dê uma resposta de primeira ordem em malha fechada para
a seguinte função de transferência em malha aberta:
A resposta desejada é a de primeira ordem com tempo morto.
Passo 1
A função de transferência para a malha fechada é dada por:
Manipulando essa expressão para obter uma fórmula de síntese ara teremos::
Como desejamos uma resposta de primeira ordem com tempo morto, podemos fazer a seguinte substituição:
Fazendo a substituição, teremos:
Rearranjando:
Passo 2
Fazendo a ubstiuição da função de transferência da planta dada no enunciado:
Agora que chegamos nesse ponto, temos um problema.
O termo exponencial dificulta um pouco nossa vida, e temos que dar um jeito de tirar ele daí.
Uma das possibilidades é fazer a aproximação:
Mas preste atenção, essa aproximação é válida apenas para pequenos valores de .
Substituindo na nossa FT:
Passo 3
Vamos agora rearranjar a expressão que encontramos para que ela possa ser comparada à de um controlador PI:
E a função de transferência genérica do controlador PI é:
Portanto, por comparação: