- Encontre uma parametrização para a superfície obtida girando-se o círculo , em torno do eixo . Esta superfície é chamada toro.
- Encontre um vetor normal a esta superfície
- Esta superfície é regular?
Passo 1
a) Já sabemos que, quando aparecer essa história de rodar uma função em torno de algum eixo, estamos tratando de superfície de revolução né? Essa está rodando em torno do eixo , portanto vamos colocar aquele fator de giro nos eixos e .
O gráfico da nossa superfície de rotação é esse aqui:
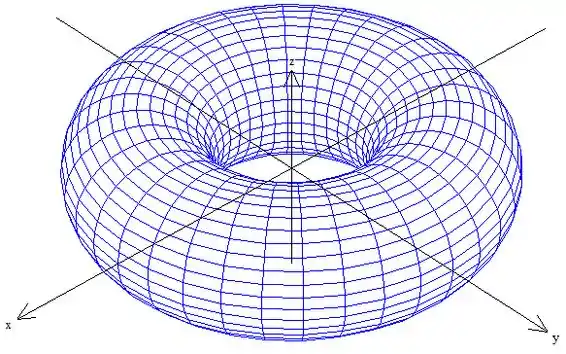
Passo 2
Para conseguir parametrizar a superfície, precisamos antes obter nosso e certo? Vamos ver a nossa equação da circunferência inicial:
Pela relação fundamental trigonométrica
Temos que
Como é o círculo inteiro que está rodando, temos que
Passo 3
Agora só falta substituir tudo na fórmula! Como rodamos no eixo , o fator de giro entra nos eixos e , e a nossa parametrização fica assim:
Passo 4
b) O vetor normal a uma superfície parametrizada por é dado por:
Resolvendo o produto vetorial,
Passo 5
c) Uma superfície é regular se for diferente de zero para os valores do domínio da superfície. Como:
Vamos supor que seja igual a a zero, olhando pro termo em temos que , logo , depende de qual ângulo pegarmos, certo?
Bom, olhando pros termos em e :
Para que ambos sejam iguais a zero, precisaria existir um ângulo em que e , o que sabemos que não existe! Portanto a normal nunca vai ser nula.
Assim, para todo o domínio, a superfície é regular!
Resposta
(a)
(b)
(c) A superfície é regular