Superfície Regular e Orientável
Produzido por Arthur Melo de AlmeidaTeoria
E aí, galera! Vamos continuar aprofundando nosso conhecimento sobre superfícies, e neste tipo vamos aprender mais alguns conceitos novos!
Mas antes vamos fazer uma revisãozinha sobre vetor normal.
Vetor normal
Bem galera já falamos sobre como obter o vetor normal a superfície lembra? Se não lembra, não tem problema eu te falo de novo. Se a gente tem uma superfície parametrizada com , calculamos o vetor normal fazendo isso aqui:
Se quisermos então o vetor normal de
Ficamos com
Lembra sempre daquele macetinho: se tivermos uma parametrização explícita, aquela em que fazíamos
A fórmula do vetor normal já está pronta, basta escrever
Agora que já relembramos como calcular o vetor normal, vamos das aplicações!
Superfícies Regulares
A primeira aplicação do vetor normal que vamos aprender agora é saber se uma superfície é regular ou não! Mas o que é uma superfície regular? Então, a gente diz que uma superfície é regular quando todos os vetores normais a ela são diferentes de zero.
E como a gente descobre se uma superfície é regular? Opa, vamos aprender com o exemplo logo abaixo!
Exemplo: A superfície é regular em todos os pontos?
O que a gente quer saber aqui então é se todos os vetores normais são diferentes de zero. Então para responder isso, vamos de um passo a passo.
Passo 1: Parametrizar a superfície
A superfície dada foi .
Vamos utilizar as coordenadas cilíndricas aqui, , , , o que nos dá:
Passo 2: Calcular e
Passo 3: Calcular
Passo 4: Ver se
Então galera, para o vetor nunca ser zero, ele nunca poderá zerar as três entradas. Como assim? Ele nunca poderá dar .
Repara que é uma variável que se repete nas três entradas, ou seja, o vetor será nulo quando
Portanto, essa superfície não é regular quando . Vamos dar uma olhada no gráfico dessa superfície para ficar mais claro,
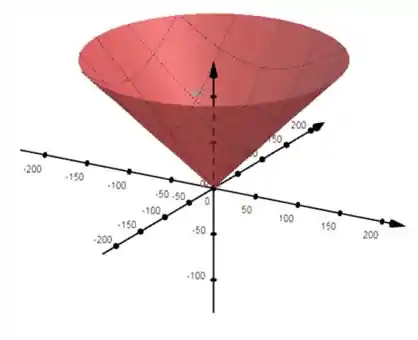
Repara que a superfície tem um “bico” na origem. Sempre que isso acontecer a superfície não será regular naquele ponto!
Generalizando, podemos dizer que uma superfície parametrizada é regular em um ponto se
Podemos dizer também que a superfície não apresenta “bicos”, ou seja, é chamada lisa.
Superfície Orientável
Vamos ver mais uma propriedade da superfície que pode ser definida pelos vetores normais!
Dizemos que uma superfície parametrizada é orientável quando é possível fixar um campo de vetores normais não nulos e contínuos.
Na prática, se a figura pode voltar ao estado original invertido, a superfície diz-se não orientável; se não, a superfície diz-se orientável. Para ficar mais claro, da uma olhada na figura abaixo,
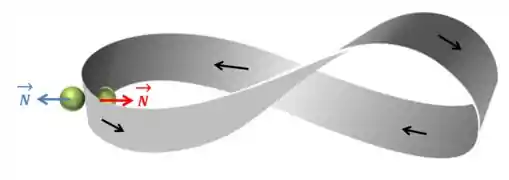
A bolinha verde representa um ponto da superfície e inicialmente ela tem seu vetor normal apontado para fora (em azul). Agora vamos andar com essa bolinha sobre a superfície seguindo o fluxo das setinhas pretas. Repara que quando chegamos ao mesmo ponto a bolinha verde estará do outro lado da superfície e seu vetor normal estará apontado para dentro (em vermelho). Ou seja, o seu estado original foi invertido.
Em resumo, se o vetor normal da superfície regular for uma função vetorial contínua então a superfície é orientável! Esse conceito é importante para usar alguns teoremas que iremos aprender!
Orientação relativa entre superfícies e curvas.
Um conceito importante em orientação é a orientação relativa entre superfícies abertas e suas borda.
Seja uma superfície orientável, dizemos que o bordo, sua curva de fronteira, está orientado positivamente se a superfície está à esquerda de uma pessoa que anda pelo bordo!
Ficou difícil de entender assim, então vamos dar uma olhada na figura e ler novamente!
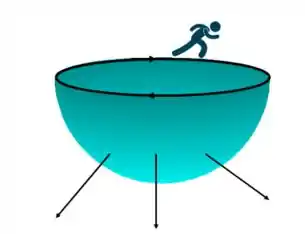
Se a superfície estiver à direita da pessoa, então dizemos que é orientado negativamente!
Se você conhece a Regra da Mão Direita, muito utilizada na Física, pode usá-la aqui! O conceito é o mesmo: quando seu polegar direito apontar no sentido da curva , seus outros dedos, que vão “furar” a superfície devem estar no sentido de . Dessa forma, a curva estará orientada positivamente.
Superfícies Regulares
Superfície Orientável
Orientação relativa entre superfícies e curvas.
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 254-6. Modificada
Considere a superfície parametrizada por
- Encontre uma expressão para um vetor normal à superfície
- Esta superfície é regular?
Passo 1
a) O vetor normal a uma superfície parametrizada por é dado por:
Resolvendo o produto vetorial,
Passo 2
b) Uma superfície é regular se for diferente de zero para os valores do domínio da superfície. Como:
Não tem , pois não existe valor de tal que e ao mesmo tempo. Então, a superfície é regular!
Resposta
(a)
(b) A superfície é regular
Exercício Resolvido #2
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 253-2 – Modificado
- Encontre uma parametrização para a superfície obtida girando-se o círculo , em torno do eixo . Esta superfície é chamada toro.
- Encontre um vetor normal a esta superfície
- Esta superfície é regular?
Passo 1
a) Já sabemos que, quando aparecer essa história de rodar uma função em torno de algum eixo, estamos tratando de superfície de revolução né? Essa está rodando em torno do eixo , portanto vamos colocar aquele fator de giro nos eixos e .
O gráfico da nossa superfície de rotação é esse aqui:
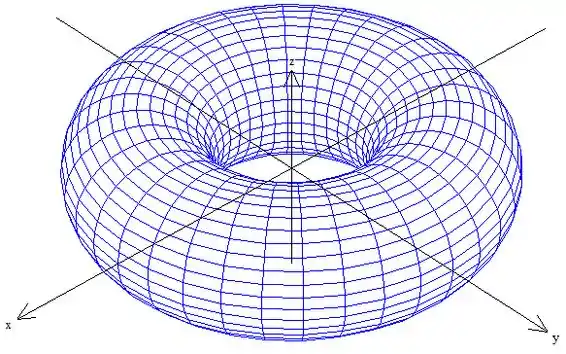
Passo 2
Para conseguir parametrizar a superfície, precisamos antes obter nosso e certo? Vamos ver a nossa equação da circunferência inicial:
Pela relação fundamental trigonométrica
Temos que
Como é o círculo inteiro que está rodando, temos que
Passo 3
Agora só falta substituir tudo na fórmula! Como rodamos no eixo , o fator de giro entra nos eixos e , e a nossa parametrização fica assim:
Passo 4
b) O vetor normal a uma superfície parametrizada por é dado por:
Resolvendo o produto vetorial,
Passo 5
c) Uma superfície é regular se for diferente de zero para os valores do domínio da superfície. Como:
Vamos supor que seja igual a a zero, olhando pro termo em temos que , logo , depende de qual ângulo pegarmos, certo?
Bom, olhando pros termos em e :
Para que ambos sejam iguais a zero, precisaria existir um ângulo em que e , o que sabemos que não existe! Portanto a normal nunca vai ser nula.
Assim, para todo o domínio, a superfície é regular!
Resposta
(a)
(b)
(c) A superfície é regular
Exercício Resolvido #3
Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1182 - 25
A superfície da figura abaixo é orientável? Explique seu raciocínio.
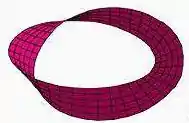
Passo 1
Sim, ela é orientável. Imagine um vetor normal a superfície e ande com o vetor ao longo de toda a superfície, assim, é possível ver que a superfície tem dois lados tornando ela orientável.
"Resposta
Ei, a resposta está no passo a passo :)