Esforços Combinados e o Estado Plano de Tensões
Produzido por Pablo RicardoTeoria
Introdução
Nos assuntos anteriores, vimos como as forças normais e os momentos fletores em uma peça geram nela tensões normais , de acordo com as fórmulas:
E como as forças cortantes e os torques internos em uma peça geram nela tensões cisalhantes , de acordo com as fórmulas:

Agora...
Ao estudar essas tensões e , nós sempre estudamos elas separadamente:
- Em alguns exercício, estudamos a tensão devido à força normal ;
- Em outros, estudamos a tensão cisalhante devido à força cortante ;
- Etc.
Mas na vida real, a verdade é que um único problema pode envolver vários desses esforços internos , , e :

Consequentemente, vão haver várias tensões e em um problema desses de esforços combinados.
E aí a má notícia é que nós não podemos simplesmente considerar essas tensões e separadamente.
![]()
Temos que considerar essas tensões e juntas.
Temos que saber como elas interagem em um ponto.
E a base para fazermos tudo isso é saber como desenhar essas tensões e em um ponto de uma peça, que é o que vamos ver nesse tópico!
Exemplo
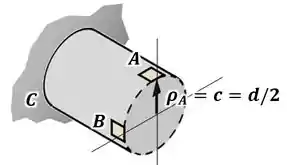
Para ver como isso funciona na prática, vamos dizer que nós precisamos descrever as tensões no ponto da imagem abaixo:
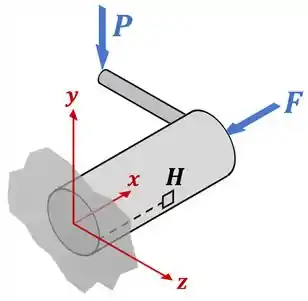
Esse é um exercício complexo, do nível que pode aparecer em um prova mais difícil.
Mas a gente consegue encarar ele.
Pensa aí!
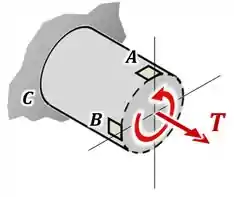
Queremos descrever as tensões no ponto , então precisamos conhecer os esforços internos na seção em que esse ponto está:
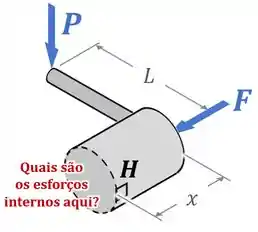
Aí, podemos lembrar que os possíveis esforços internos em uma peça são:
- A força normal , que nesse caso vai apontar para dentro da seção para equilibrar a força externa ;
- A força cortante , que nesse caso vai apontar para cima para equilibrar a força externa para baixo;
- O momento fletor , que nesse caso vai comprimir o inferior da seção, de forma a equilibrar o momento gerado pela força com o braço ;
- E o torque interno , que nesse caso vai girar no sentido horário, de forma a equilibrar o momento gerado pela força com o braço .
Dessa forma, a nossa seção transversal fica assim:
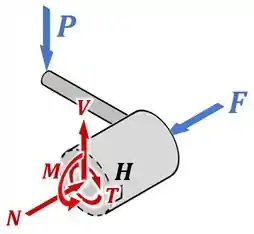
Esse desenho acima é difícil de fazer e entender, então é comum representar esse mesmo desenho de uma forma mais simples assim em um exercício:
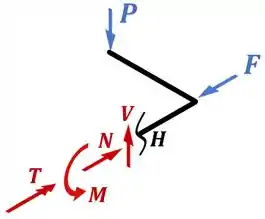
Cálculo das Tensões
Em seguida, podemos calcular as tensões causadas por cada um desses esforços internos no nosso ponto , usando as fórmulas e conhecimentos que vimos nos assuntos anteriores.
Vamos lá lembrar de tudo!
Primeiro, devido à força normal apontando para dentro da seção, vai surgir uma tensão normal média de compressão em toda a seção, inclusive no ponto :
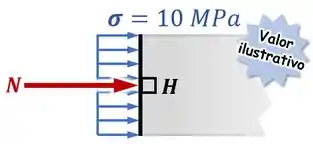
Segundo, devido à força cortante para cima, vamos ter uma tensão cisalhante , também para cima.
Essa tensão vai tem uma distribuição que é máxima justamente no meio da seção circular, que é onde fica o nosso ponto :
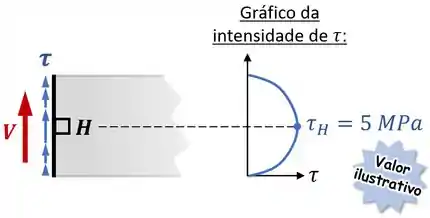
Terceiro, devido ao momento fletor , vamos ter uma tensão normal de flexão que é nula na linha neutra, onde fica o ponto :
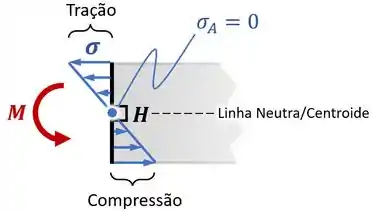
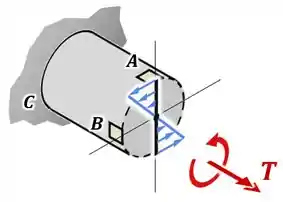
E finalmente, devido ao torque interno , vamos ter uma tensão de torção que é máxima e vai apontar para baixo no ponto :

Desenho das Tensões no Ponto
Agora, já estamos prontos para desenhar como ficam as tensões e no nosso ponto , que vamos representar como um quadrado muito pequeno:

Aí, usando os valores ilustrativos que acabamos de “encontrar”, podemos indicar quais são as tensões nesse quadrado .
De tensão normal, só temos a tensão de causada pela força normal . Adicionando essa tensão ao nosso quadrado, ele fica assim:
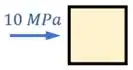
Mas essa tensão sozinha faria o nosso quadrado andar para o lado, o que não deve ser possível.
Então equilibramos ela com uma tensão oposta do outro lado:

Já de tensão cisalhante, temos a tensão de para cima causada pela força cortante e a tensão de para baixo causada pelo torque interno .
Dessa forma, a resultante no nosso quadrado é uma tensão cisalhante de para baixo:
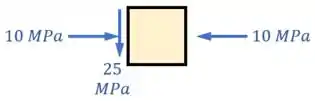
Mas essa tensão cisalhante sozinha faria o quadrado andar para abaixo.
Então devemos equilibrar ela com outra tensão cisalhante oposta do outro lado:
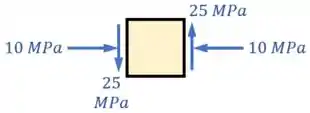
Só que agora essas duas tensões cisalhantes vão fazer o quadrado girar.
Então devemos equilibar elas com tensões cisalhantes iguais, mas que gerem rotação no sentido oposto, nos outros dois lados do quadrado:
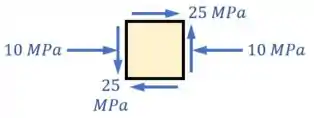
Por fim, é desnecessário escrever mais de uma vez o valor do par de tensões normais ou o valor das tensões cisalhantes, então podemos deixar esse desenho assim:
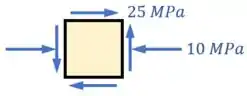
E pronto!
Esse desenho acima é o estado plano de tensões para o nosso ponto .
Caso Geral
Para um ponto qualquer, o estado plano de tensões é definido assim:
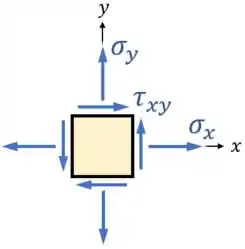
Onde:
- é a tensão normal na horizontal;
- é a tensão normal na vertical;
- & é a tensão cisalhante.
Sendo que as tensões são positivas do jeito que foram desenhadas acima:
- As tensões são positivas quando apontam para fora da peça;
- E é positiva quando suas setas se concentram no 1° e 3° quadrante;
Por fim, se quisermos, podemos definir o estado de tensões do nosso ponto a partir desse caso geral “”.
Para tanto, basta comparar as duas imagens:
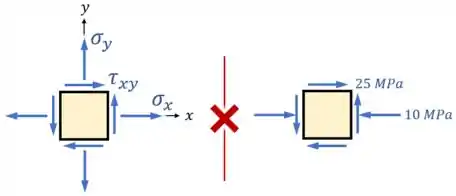
Fazendo isso, encontramos que para o ponto :
Sendo que é interessante ver como nesse caso é negativo, uma vez que a seta de no estado plano de tensões para está no sentido oposto da convenção de do caso geral.
Exemplo
Desenho das Tensões no Ponto
Caso Geral
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 335-9.31. (Adaptado)
O eixo tem diâmetro e está sujeito às cargas mostradas. Faça um desenho do estado plano de tensões para um ponto na superfície desse eixo.

Passo 1
O que está acontecendo?
O eixo tem um diâmetro .
As forças axiais nele vão gerar em todas as seções dele uma força interna normal :
...uma vez que essas forças são forças de compressão.
Essa força interna normal por sua vez vai gerar em todos os pontos dessas seções uma tensão normal média .
Dessa forma, já sabemos que vai haver em um ponto na superfície desse eixo uma tensão normal média .
Além disso...
Os torques no eixo vão gerar nele torques internos (também conhecidos como momentos torsores dependendo dos seus professores):
Como mostra a análise dos esforços internos abaixo:
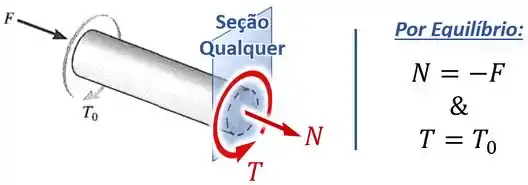
Esse torque interno , por sua, vez, vai gerar nos pontos dessa seção uma tensão de cisalhamento de acordo com a fórmula da torção:
Onde:
- é a distância do centro da seção até o ponto em que se quer saber a tensão ;
- & é o momento de inércia polar da seção e é dado pela fórmula:
...para uma seção circular de raio .
(No nosso caso, vamos usar , uma vez que o raio é a metade do diâmetro.)
E o que é que o exercício quer?
Ele quer que a gente desenhe o estado plano de tensões em um ponto na superfície desse eixo.
Para tanto, devemos escolher um ponto qualquer na superfície desse eixo, como um logo atrás da seção qualquer que fizemos, por exemplo:

Com isso, podemos agora estudar como são as tensões e nesse ponto.
Aí, conhecendo essas tensões, vamos poder desenhar os resultados em um elemento quadrado representando o ponto.
E aí esse desenho vai ser o estado plano de tensões pedido pelo exercício!
Passo 2
Então vamos lá!
Vamos começar calculando a tensão normal causada pela força normal .
Aplicando a fórmula da tensão normal média, temos:
Aí, substituindo:
- ;
- E a área da seção transversal circular de diâmetro , ,
Encontramos que:
O que significa que o nosso ponto é comprimido na horizontal (que é a direção da força normal ) por uma tensão normal de intensidade :
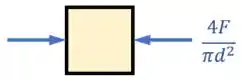
Ok!
Passo 3
Agora, vamos encontrar a tensão cisalhante causada pelo torque interno .
Aplicando a fórmula da torção, temos:
Aí, substituindo:
- ;
- & ,
...e percebendo que para um ponto na superfície do nosso eixo, a distância vai ser igual ao raio do eixo, vamos ter que:
Simplificando isso, temos:
Finalmente, substituindo , encontramos que a tensão de cisalhamento no nosso ponto é:
Por último, ainda precisamos entender qual vai ser a direção dessa tensão cisalhante .
Daí que, olhando para o sentido do torque interno e para o nosso ponto:

...vemos que a tensão cisalhante causada por vai apontar para baixo no lado direito desse ponto que escolhemos:
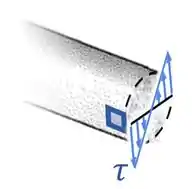
Aí, representando isso no nosso ponto, temos:
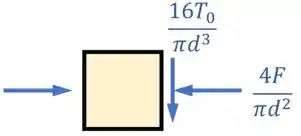
Por fim, para equilibrar essa tensão, temos que desenhar outras 3 tensões cisalhantes nos outros lados do elemento:
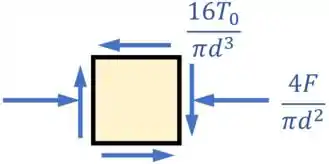
E pronto!
Esse desenho acima é o estado plano de tensões para um ponto na superfície desse eixo e é a nossa resposta para o exercício.
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 357-9.96. (Adaptado)
O parafuso está preso a seu suporte em . Se a força de for aplicada à chave para apertá-lo, determine as tensões normais e de cisalhamento no ponto . Além disso, represente os resultados sobre um elemento localizado nesse ponto. A haste tem diâmetro de .
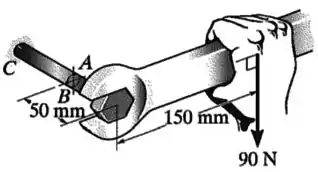
Passo 1
O que está acontecendo?
A força de aplicada na chave vai gerar uma série de esforços internos na seção de diâmetro onde se encontram os pontos e .
Esses esforços internos, por sua vez, vão gerar tensões normais e tensões cisalhantes nesses pontos.
E o que é que o exercício quer?
Ele quer que a gente determine essas tensões e resultantes no ponto .
Em seguida, ele ainda quer que a gente represente esses resultados desenhando o estado plano de tensões para esse ponto, como ilustrado na imagem abaixo:
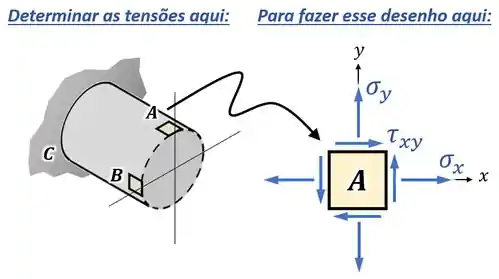
Então, para resolver esse exercício...
Devemos começar fazendo uma seção na peça no local onde está esse ponto .
Dessa forma, poderemos analisar e determinar os esforços internos que atuam nesse seção.
Com isso, vamos poder identificar as tensões e causadas por cada um desses esforços internos.
E, assim, vamos conseguir fazer os desenhos do estado plano de tensões para o ponto .
Passo 2
Então vamos começar fazendo uma análise dos esforços internos na seção onde se encontra o ponto .
Para tanto, podemos representar as peças de uma forma simplificada e fazer uma seção na região desse ponto:
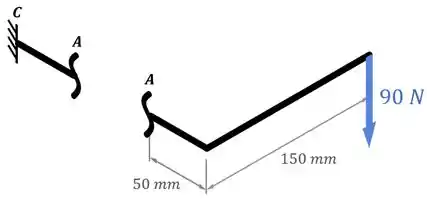
Feito isso, devemos identificar quais vão ser os esforços internos que vão surgir nessa seção.
Então lembra aí!
Os possíveis esforços internos são:
- Força normal ;
- Força cortante ;
- Momento fletor (ou );
- E torque interno (ou momento torsor ).
Desenhando esses esforços internos na nossa seção, o desenho acima fica assim:
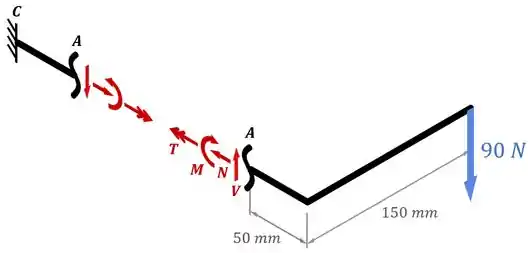
Lembrando que dependendo da convenção dos seus professores, o torque interno pode ser desenhado também entrando para dentro das peças.
Passo 3
Agora, precisamos calcular os valores desses esforços internos , , e .
Para tanto, podemos aplicar condições de equilíbrio para toda a parte direita das peças:
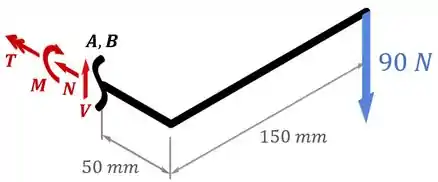
Primeiro, aplicando o equilíbrio de forças na horizontal, temos:
A única força na horizontal é a força normal , então temos que:
Ou seja, não há força normal nesse seção.
Em seguida, aplicando o equilíbrio de forças na vertical, temos:
Na vertical, temos a cortante para cima e a força de para baixo.
Dessa forma, esse somatório acima fica assim:
O que significa que:
Já para determinar o valor do momento fletor , precisamos aplicar o equilíbrio de momentos em relação ao ponto :
Em relação a esse ponto, nós vamos ter um momento no sentido horário () causado pela força de com um braço de e o momento também no sentido horário ().
Dessa forma, esse somatório de momentos acima fica assim:
O que significa que:
O que dá:
Por fim, para determinar o valor do torque interno , precisamos fazer um equilíbrio de torques:
Em relação ao eixo principal do parafuso, nós vamos ter um torque no sentido horário () causado pela força de com um braço de , além do próprio torque interno , também no sentido horário ().
Então o nosso somatório de torques fica assim:
O que significa que:
Passo 4
Agora que conhecemos os esforços internos na seção do ponto :
...podemos calcular as tensões causadas por esses esforços internos.
Nesse passo, vamos começar analisando a tensão de cisalhamento causada pela força cortante .
Lembra aí!
Ela é dada pela fórmula do cisalhamento:
Onde:
- é o momento estático para a fibra em que se quer calcular a tensão ;
- é o momento de inércia da área da seção transversal;
- & é a espessura da fibra em que se quer calcular a tensão .
Aí, se a gente olhar para o nosso ponto , vamos perceber uma coisa:
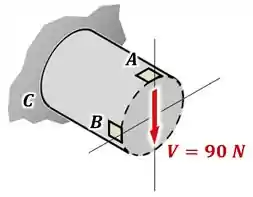
Que é: esse nosso ponto está no topo da seção!
E lá quando estudamos a fórmula do cisalhamento, vimos que o momento estático das fibras no topo e na base de uma seção é nulo.
Consequentemente, a tensão de cisalhamento devido à força cortante nos pontos dessas fibras é nula.
Ou seja:
A força cortante não vai causar nenhuma tensão no nosso ponto .
Passo 5
Em seguida, vamos ver como é a tensão causada pelo momento fletor no nosso ponto .
Lá quando estudamos flexão, vimos que a tensão normal causada por um momento fletor é dada pela fórmula da flexão:
Onde:
- é a posição do ponto em que se quer saber a tensão em relação à linha neutra;
- & é o momento de inércia da área da seção transversal.
No caso da nossa seção circular, temos que a linha neutra passa bem no meio dela:
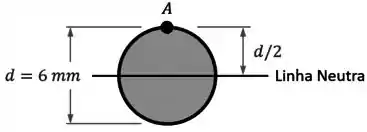
Aí, da imagem acima, vemos como a posição do nosso ponto é:
Além disso, para uma seção circular, o momento de inércia da área é dado pela fórmula:
Onde é o raio da seção e é igual à metade do diâmetro dela (), de tal forma que:
Sabendo de tudo isso, já podemos aplicar a fórmula da flexão para o nosso ponto :
Aí, substituindo:
- ;
- & ,
Temos que:
Simplificando, isso dá:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Calculando tudo isso, vamos ter um resultado em que vai dar:
Mas é o mesmo que , o que significa que:
E o que é que esse resultado significa?
Ele significa que o nosso ponto está sendo tracionado lateralmente por uma tensão normal de :
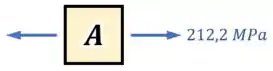
Passo 6
Por fim, podemos ver como será a tensão causada pelo torque interno .
Pelo que vimos lá em torção, sabemos que esse torque interno vai gerar na seção tensões de cisalhamento de acordo com a fórmula da torção:
Onde:
- é a distância do centro da seção até o ponto em que se quer saber a tensão ;
- & é o momento de inércia polar da seção e é dado pela fórmula:
...para uma seção circular de raio .
No nosso caso, vamos usar , uma vez que o raio é a metade do diâmetro, de tal forma que:
Aí, para o nosso ponto , a distância dele ao centro é igual ao raio da seção:
Assim, já podemos aplicar a fórmula da torção para o nosso ponto :
Substituindo:
- ;
- & ,
Temos:
Simplificando, temos:
Finalmente, substituindo os valores:
- ;
- & ,
Encontramos que:
Calculando tudo, e vendo que o resultando dessa equação vai sair em , que é o mesmo que , obtemos que:
Passo 7
Estamos quase terminando o exercício, mas ainda temos um último desafio que é saber em que sentido atua essa tensão de cisalhamento que acabamos de encontrar.
Isso porque:
- Enquanto que a fórmula da flexão é “inteligente” (ela consegue através do seu sinal de positivo ou negativo indicar se é uma tensão de tração ou compressão),
- A fórmula da torção não é “inteligente”.
Então nós temos que olhar pros desenhos que fizemos para entender qual é o sentido da tensão .
Podemos, por exemplo, olhar pro lado esquerdo do desenho que fizemos lá no começo do exercício:
Nesse desenho, a seta dupla corresponde ao torque.
Visualizando esse torque na nossa peça com o auxílio da regra da mão direita, ele fica assim:
O que significa que caso ele fosse positivo, ele geraria uma tensão que apontaria para baixo no lado direito do ponto :
Mas na realidade, o torque interno e a tensão que encontramos tem valores negativos.
Isso significa que a tensão cisalhante de intensidade no nosso ponto vai na realidade estar apontando para cima no lado direito do ponto :
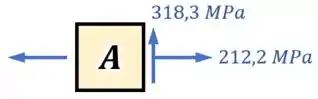
Por fim, para equilibrar esse elemento , devemos adicionar três outras tensões de cisalhamento com a mesma intensidade nos demais lados do elemento:
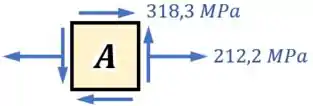
E pronto!
Esse desenho acima é o nosso estado plano de tensões para o ponto e completa nossa resposta para o exercício.
Além disso, na hora de destacar os valores das tensões no ponto para a resposta do exercício, podemos fornecer os valores de acordo com o caso geral do estado plano de tensões:
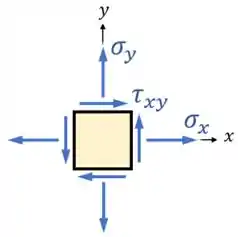
Comparando essa imagem com o nosso desenho acima, vemos que para o ponto :
Resposta
Exercício Resolvido #3
Elaboração própria
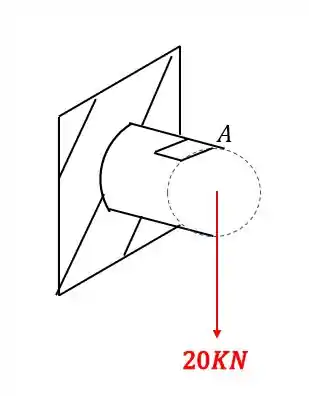
Dada a barra abaixo, determine o estado plano de tensões no ponto A que represente todos os esforços solicitantes nesse trecho.
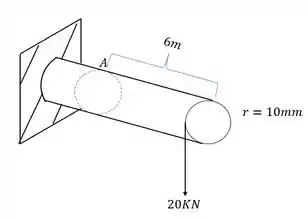
Passo 1
Nesse tipo de questão, é sempre bom tomar extremo cuidado com as contas feitas. É muito importante fazer cada parte tomando extremo cuidado. Primeiro devemos levar todos os esforços do extremo da barra para o ponto que desejamos calcular, o desenho abaixo representa como vamos fazer isso.
Primeiro olhamos a seção que temos que levar os esforços
Em seguida analisamos quais solicitações os nossos esforços produziram
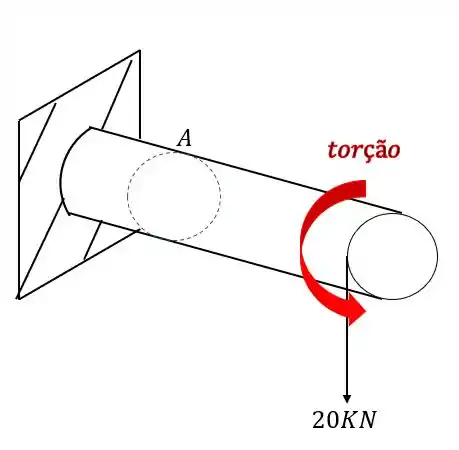
Sabemos que a nossa carga produz torção
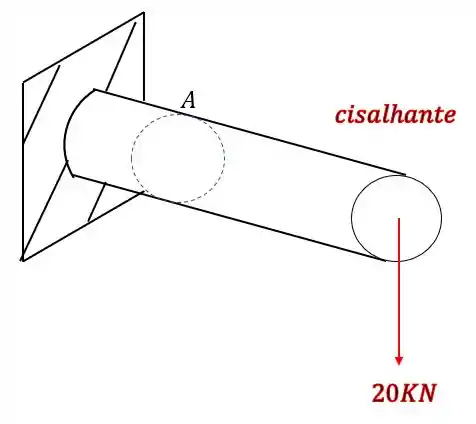
Produz cisalhante
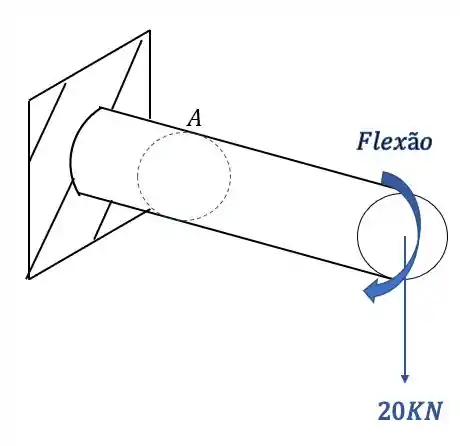
Produz flexão
Levando todos esses esforços para nossa seção, teremos que
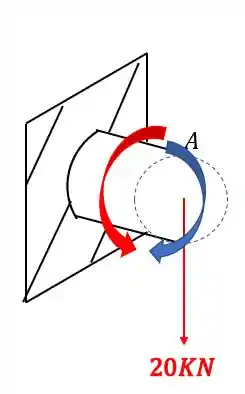
Mas da pra perceber que é difícil analisar os esforços em 3 dimensões, então pra facilitar podemos usar a regra da mão direita, em que os 4 dedos rodam na mesma direção dos momentos, e o polegar aponta na direção do vetor que usaremos pra representar, então nossa seção ficará
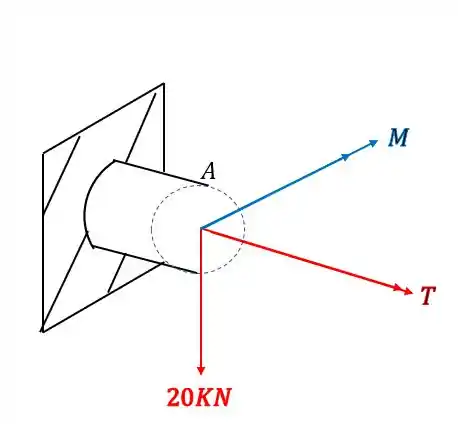
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que o momento fletor produz esforços normais, e que o torsor e cisalhante produzem esforços de cisalhamento. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação do momento fletor.
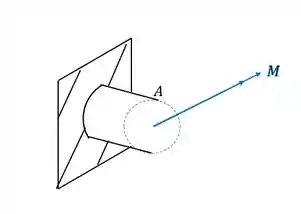
Sabemos que a fórmula que nos auxilia nesse calculo é
Sabemos que y é a distancia da linha Neutra da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é negativo, e por estar na extremidade, vale o próprio valor do raio.
Também temos que calcular o valor do momento
Sabemos pela figura que o braço de alavanca é de 6m com uma carga de 20KN
Por fim, basta determinar o valor do momento de inercia de uma barra circular, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
Olhando novamente a figura, vemos que nosso elemento é
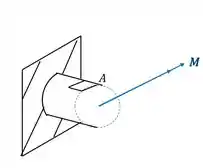
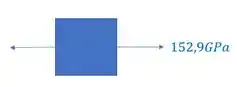
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 3
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a fórmula
Mas vamos olhar a nossa figura
Queremos o cisalhante em A, então basta você pensar no seguinte, uma das coisas pedidas nessa conta é o momento estática(S), que é a área acima do ponto que calculamos o cisalhante.
Agora pensa comigo, qual a área acima do ponto A?
Isso mesmo, não tem, logo
Se o momento estático em A é zero, podemos deduzir que
Outra forma de calcular seria lembrando do nosso diagrama, que para esforço cortante é zero nas extremidades e máximo na linha neutra. Como aqui o ponto A está na extremidade, ele vale zero, para exemplificar podemos ver isso no diagrama abaixo.
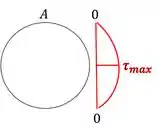
Passo 4
Por fim basta analisarmos os esforços para a ação do Torso.
Sabemos que a fórmula que nos dá isso é
Vamos ir deduzido cada valor da nossa fórmula.
Sabemos que o se trata do ponto que estamos calculando, como esse ponto esta na extremidade, o valor será o próprio raio da seção
Também temos que determinar o nosso momento torsor
Pela figura temos que
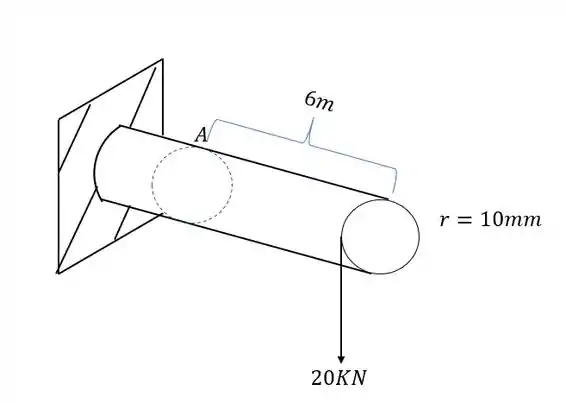
Como a nossa carga age na extremidade, basta multiplicarmos o valor da carga com a distancia dela até o centro, logo teremos que
Por fim falta o cálculo do J que é dado pela equação
Substituindo teremos que
Agora que já temos todos os valores
Vamos substituir na nossa equação principal
Mas como representamos isso no nosso elemento?
Basta apenas analisar o diagrama formado nessa figura
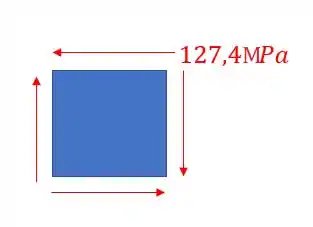
Logo a representação no nosso elemento será
Passo 5
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.
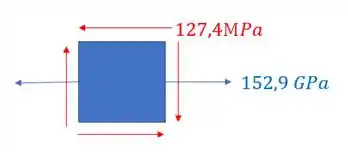
Resposta
Exercício Resolvido #4
Elaboração própria
Abaixo foi dada uma barra sujeita a ação de um esforço torso, e um esforço normal. Sabendo disso determine o estado plano de tensões no ponto A que represente os esforços no mesmo.
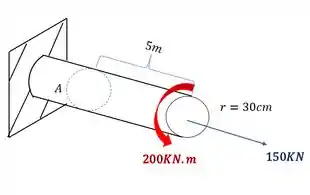
Passo 1
Nesse tipo de questão, é sempre bom tomar extremo cuidado com as contas feitas. É muito importante fazer cada parte tomando extremo cuidado. Primeiro devemos levar todos os esforços do extremo da barra para o ponto que desejamos calcular, o desenho abaixo representa como vamos fazer isso.
Primeiro olhamos a seção que temos que levar os esforços
Em seguida analisamos quais solicitações os nossos esforços produziram
Sabemos que temos torção
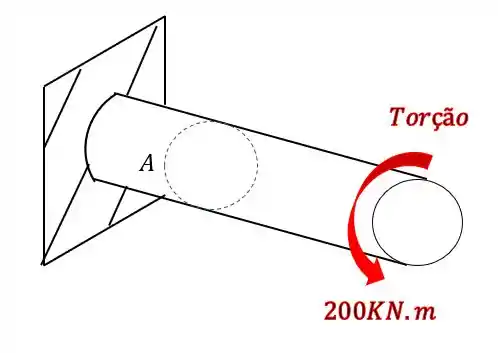
E temosNormal
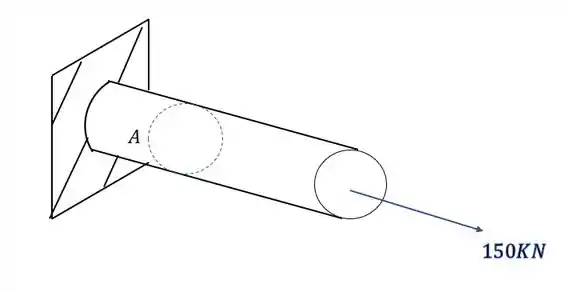
Levando todos esses esforços para nossa seção, teremos que
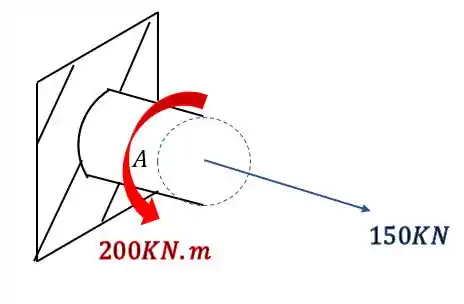
Mas da pra perceber que é difícil analisar os esforços em 3 dimensões, então pra facilitar podemos usar a regra da mão direita, em que os 4 dedos rodam na mesma direção dos momentos, e o polegar aponta na direção do vetor que usaremos pra representar, então nossa seção ficará
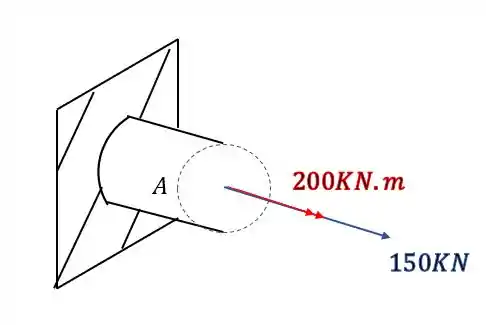
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, e que o torsor produzem esforços de cisalhamento. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
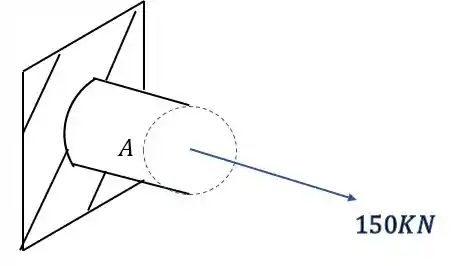
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
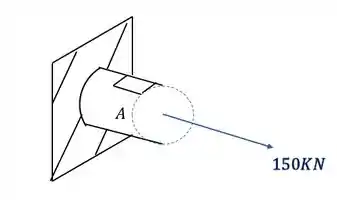

É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Por fim basta analisarmos os esforços para a ação do Torso.
Sabemos que a fórmula que nos dá isso é
Vamos ir deduzido cada valor da nossa fórmula.
Sabemos que o se trata do ponto que estamos calculando, como esse ponto está na extremidade, o valor será o próprio raio da seção
Também temos que determinar o nosso momento torsor
Pela figura temos que
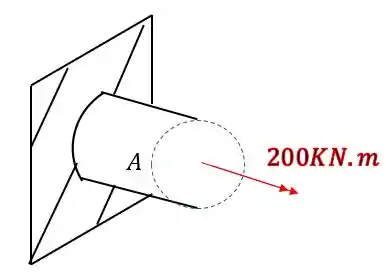
teremos que
Por fim falta o cálculo do J que é dado pela equação
Substituindo teremos que
Agora que já temos todos os valores
Vamos substituir na nossa equação principal
Mas como representamos isso no nosso elemento?
Basta apenas analisar o diagrama formado nessa figura
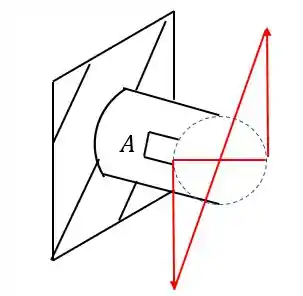
Logo a representação no nosso elemento será
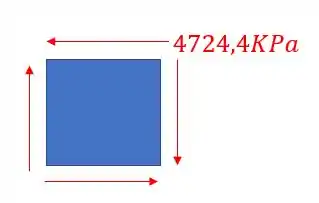
E pela convenção de sinais, quando as setas se concentram no segundo e no quarto quadrante teremos uma tensão negativa.
Passo 4
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.
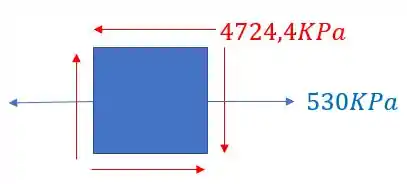
Resposta
Exercício Resolvido #5
Elaboração própria
Uma barra esta sujeita a um esforço fletor e uma carga normal. Determine dessa forma o estado plano de tensões no ponto A da barra. Seção da barra (20x20cm).
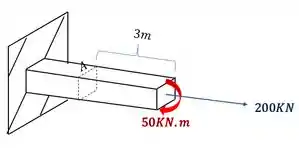
Passo 1
Nesse tipo de questão, é sempre bom tomar extremo cuidado com as contas feitas. É muito importante fazer cada parte tomando extremo cuidado. Primeiro devemos levar todos os esforços do extremo da barra para o ponto que desejamos calcular, o desenho abaixo representa como vamos fazer isso.
Primeiro olhamos a seção que temos que levar os esforços
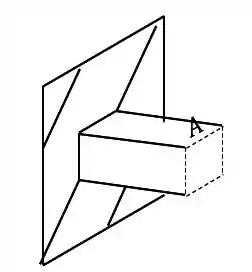
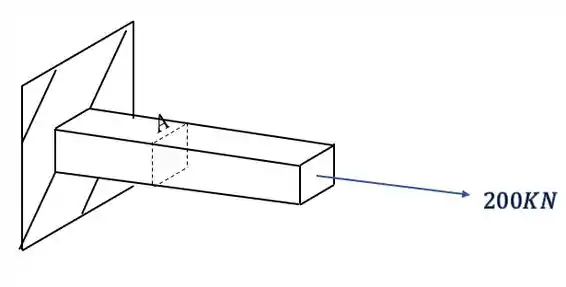
Em seguida analisamos quais solicitações os nossos esforços produziram
Sabemos que temos força Normal
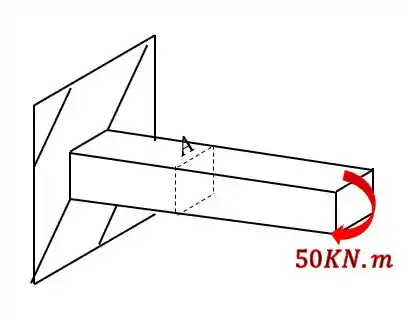
Sabemos que temos esforço fletor também
Levando todos esses esforços para nossa seção, teremos que
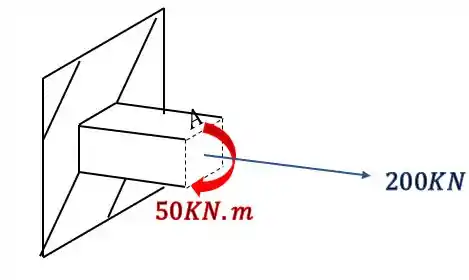
Mas da pra perceber que é difícil analisar os esforços em 3 dimensões, então pra facilitar podemos usar a regra da mão direita, em que os 4 dedos rodam na mesma direção dos momentos, e o polegar aponta na direção do vetor que usaremos pra representar, então nossa seção ficará
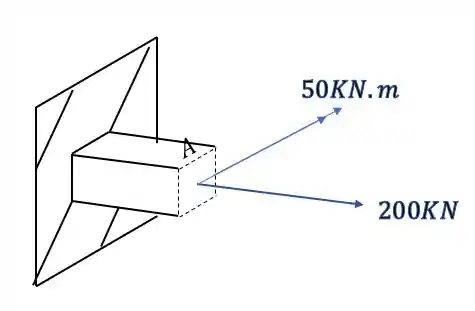
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
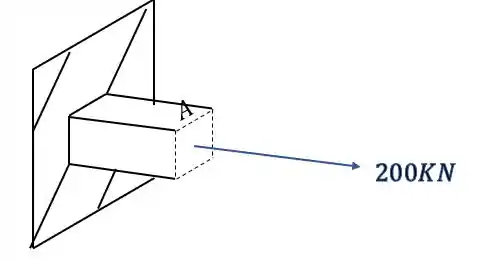
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
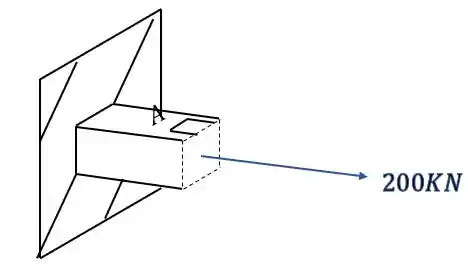
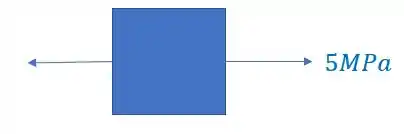
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor.
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância da linha neutra da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é negativo, e por estar na extremidade, vale o próprio valor da metade do lado.
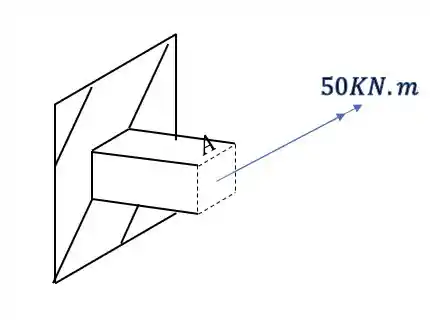
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é
Por fim, basta determinar o valor do momento de inercia de uma barra quadrada, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
Olhando novamente a figura, vemos que nosso elemento é
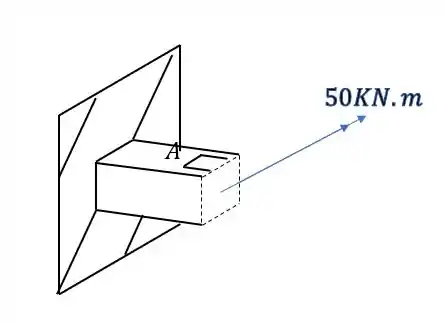
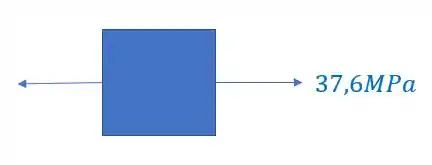
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.
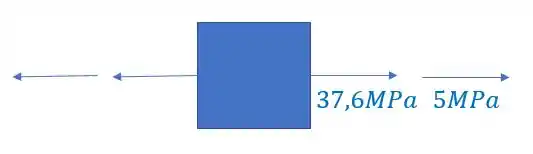
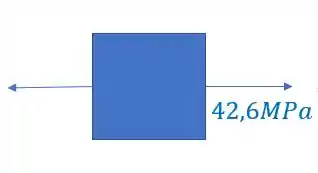
Resposta
Exercício Resolvido #6
Elaboração própria
O pórtico abaixo está sujeito aos esforços mostrados. Dessa forma, determine o estado plano de tensões que age no ponto A desse pórtico.
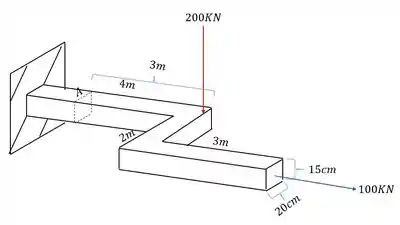
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
Analisando primeiro a carga de 100KN vemos que ela produz uma força normal, e também um esforço fletor como mostra a figura abaixo.
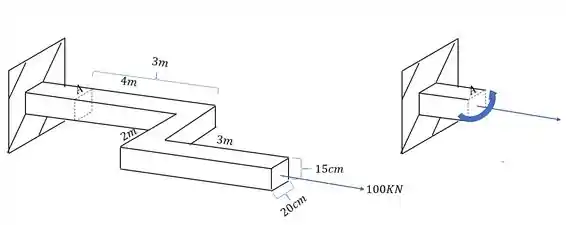
podemos ver também que a carga de 200KN produz na nossa seção uma componente cisalhante, e também um esforço fletor como mostrado na figura abaixo
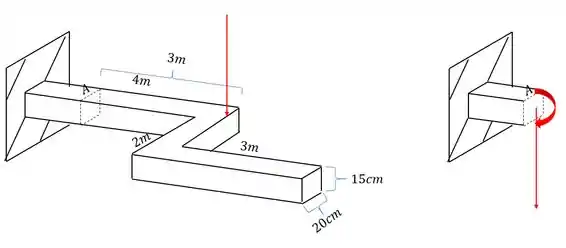
O que podemos perceber é que seria muito complexo analisar a figura com os esforços em 3 dimensões, então vamos facilitar e usar a regra da mão direita para colocarmos no lugar dos vetores momentos, os vetores que ficam na direção do nosso dedão. Fazendo isso teremos que o nosso elemento ficará
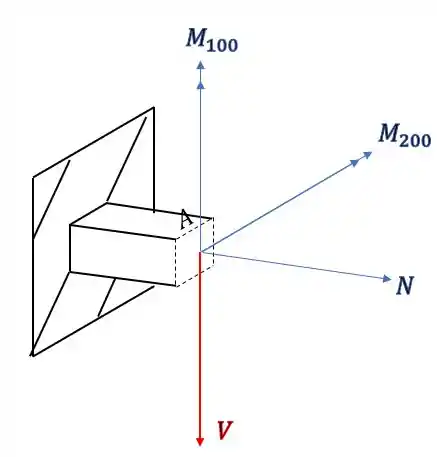
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes. Então vamos dividir essa segunda parte da solução em duas parte.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
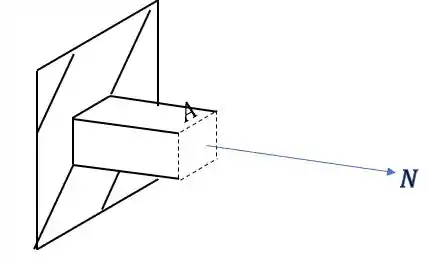
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
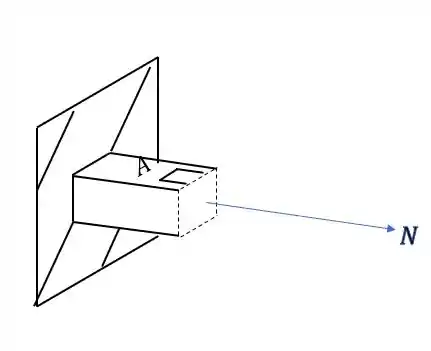
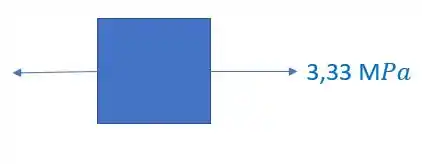
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor devido a carga de 200KN.
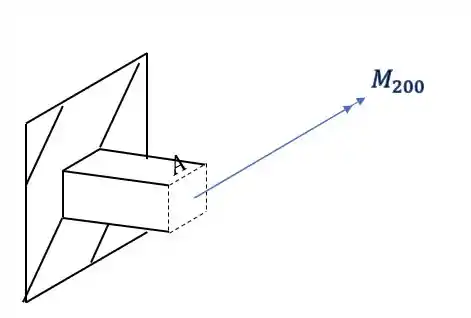
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é positivo, e por estar na extremidade, vale o próprio valor da metade do lado.
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é o braço de alavanca da carga de 200KN e o próprio valor do braço de alavanca, e é negativo pois é contrario ao sistema de eixos que adotamos.
Por fim, basta determinar o valor do momento de inercia de uma barra retangular, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
Olhando novamente a figura, vemos que nosso elemento é
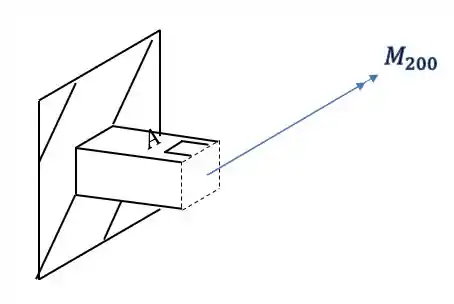
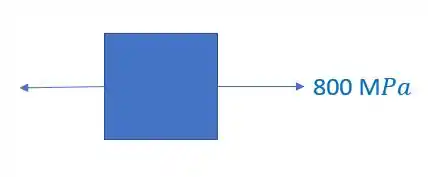
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Vamos calcular os esforços normais devido a ação do momento fletor da carga de 100.
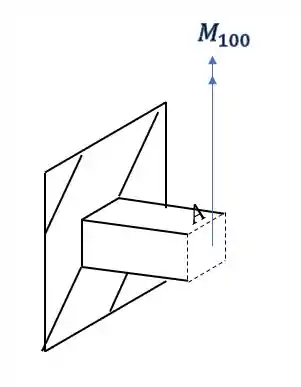
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância da linha neutra da peça até o ponto calculado, como esse ponto está na linha neutra, sabemos que seu valor é zero
Isso acontece porque, como o vetor momento está apontando na vertical, a linha neutra também estará na vertical. Basta utilizarmos a regra da mão direita e vamos perceber que o eixo de rotação nesse caso vai estar na vertical, com o ponto A logo em cima dele.
Se temos y=0 então substituindo só esse valor na fórmula principal teremos que
Logo o momento fletor produzido pela carga de 100KN não interfere no funcionamento do elemento do estado plano de tensões.
Aqui vale ressaltar que para momentos fletores máximos devemos fazer os cálculos para os pontos nas extremidades da peça, enquanto que o valor do momento sobre a linha neutra é zero.
Passo 5
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a fórmula
Mas vamos olhar a nossa figura
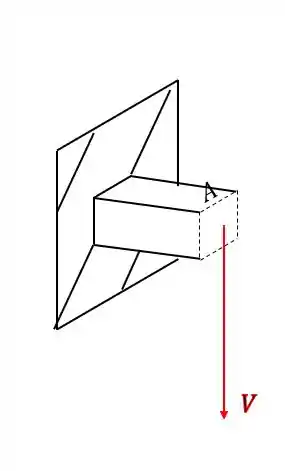
Queremos o cisalhante em A, então basta você pensar no seguinte, uma das coisas pedidas nessa conta é o momento estática(S), que é a área acima do ponto que calculamos o cisalhante.
Agora pensa comigo, qual a área acima do ponto A?
Isso mesmo, não tem, logo
Se o momento estático em A é zero, podemos deduzir que
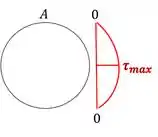
Outra forma de calcular seria lembrando do nosso diagrama, que para esforço cortante é zero nas extremidades e máximo na linha neutra. Como aqui o ponto A está na extremidade, ele vale zero, para exemplificar podemos ver isso no diagrama abaixo.
Passo 6
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.

Resposta
Exercício Resolvido #7
Elaboração própria
A barra de aço circular abaixo, de diâmetro 20mm, foi sujeita ao carregamento mostrado na figura. Determine o estado plano de tensões que ocorrem no ponto A da nossa barra.
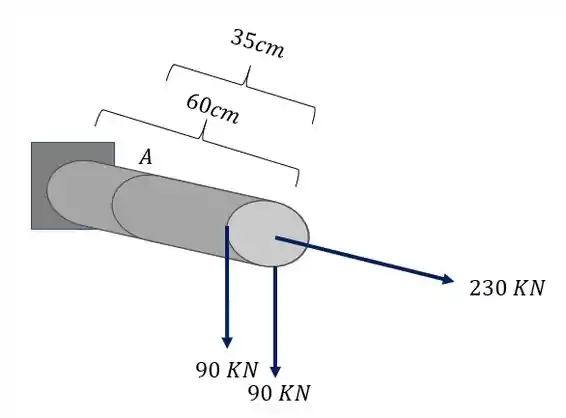
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
Analisando primeiro a carga de 90KN que está deslocada vemos que ela produz uma força cortante, um esforço torçor e também um esforço fletor como mostra a figura abaixo.
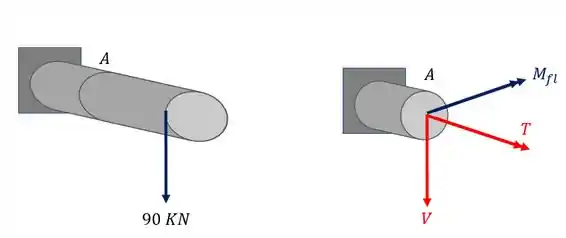
podemos ver também que a carga de 90 KN não deslocada produz na nossa seção uma componente cortante e também um momento fletor
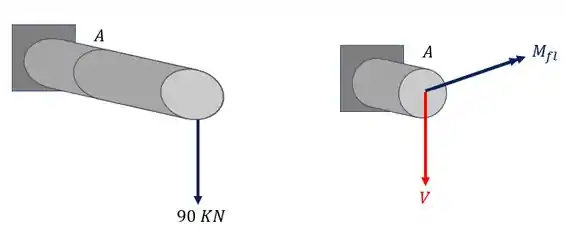
Além disso podemos ver que a carga de 230 KN não deslocada produz na nossa seção apenas uma componente, que nesse caso é uma força normal, como podemos ver na nossa figura
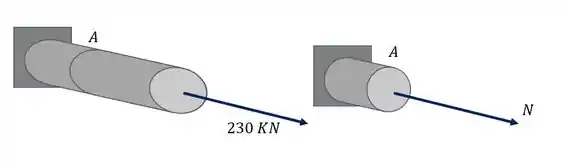
Analisando a nossa seção com todos os esforços juntos teremos que
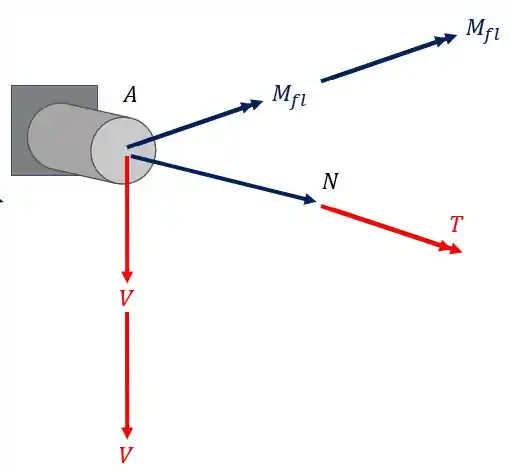
Nesse caso tanto o cortante quanto o momento fletor são iguais pois ambas as cargas são iguais e estão a mesma distância da nossa seção, logo não precisamos usar características diferentes já que ambos os valores são idênticos.
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes assim como o torsor. Então vamos dividir essa segunda parte da solução em duas partes.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
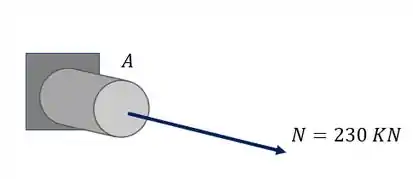
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Se o diâmetro é 20mm o raio será metade disso, ou seja, 10mm, então temos que
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
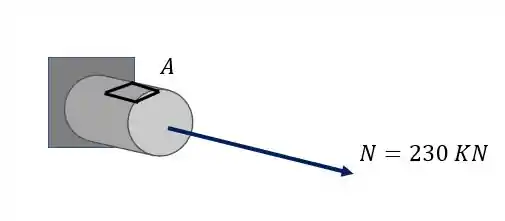
O nosso elemento isolado com a tensão será
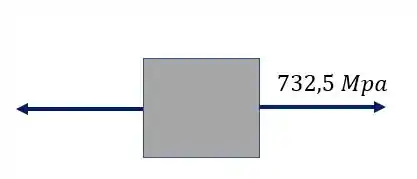
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor. Mas perceba o seguinte, como temos dois momentos fletores iguais, basta calcularmos apenas um dos momentos e multiplicar o valor por dois. Temos dois momentos fletores causados pela carga de 90 KN e ambas possuem o mesmo braço de alavanca, por isso ambos são iguais.
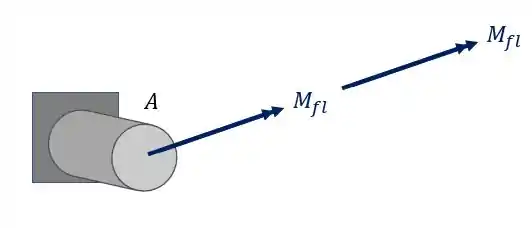
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima, sabemos que seu sinal é positivo, e por estar na extremidade, vale o próprio valor raio.
Também temos que calcular o valor do momento
Sabemos pela figura que o nosso momento fletor é o braço de alavanca da carga de 90KN e o próprio valor do braço de alavanca, além é claro de ser negativo por ser contrario aos eixos adotados
Como são dois momentos teremos que
Por fim, basta determinar o valor do momento de inercia de uma barra circular, que é dada por
Substituindo os valores do enunciado teremos que
Substituindo na nossa equação teremos que
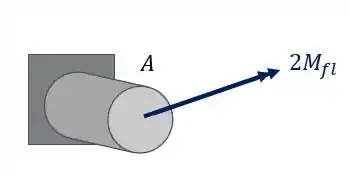
Olhando novamente a figura, vemos que nosso elemento é
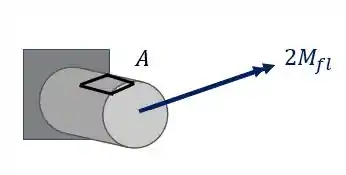
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento. Você também pode perceber isso fazendo a regra da mão direita no ponto A e vendo que ele é tracionado quando fazemos isso.
Passo 4
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a f��rmula
Mas vamos olhar a nossa figura. Lembre-se que os nossos cortantes são iguais, assim teremos que
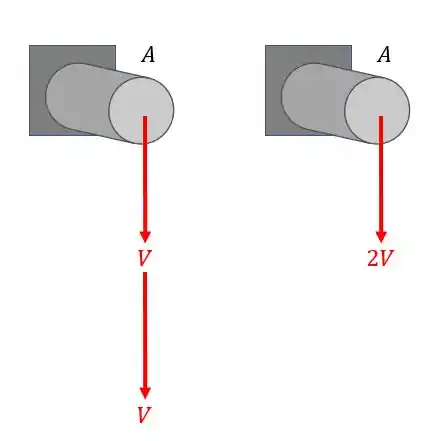
Queremos o cisalhante em A, então basta você pensar no seguinte, uma das coisas pedidas nessa conta é o momento estática(S), que é a área acima do ponto que calculamos o cisalhante.
Agora pensa comigo, qual a área acima do ponto A?
Isso mesmo, não tem, logo
Se o momento estático em A é zero, podemos deduzir que
Outra forma de calcular seria lembrando do nosso diagrama, que para esforço cortante é zero nas extremidades e máximo na linha neutra. Como aqui o ponto A está na extremidade, ele vale zero, para exemplificar podemos ver isso no diagrama abaixo.
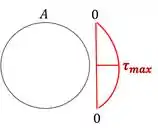
Passo 5
Por fim basta analisarmos os esforços para a ação do Torso.
Sabemos que a fórmula que nos dá isso é
Vamos ir deduzido cada valor da nossa fórmula.
Sabemos que o se trata do ponto que estamos calculando, como esse ponto está na extremidade, o valor será o próprio raio da seção
Também temos que determinar o nosso momento torsor
Pela figura temos que
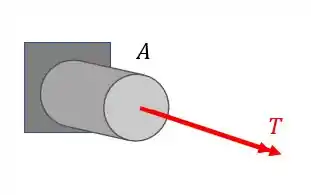

teremos que
Por fim falta o cálculo do J que é dado pela equação
Substituindo teremos que
Agora que já temos todos os valores
Vamos substituir na nossa equação principal
Mas como representamos isso no nosso elemento?
Basta apenas analisar o diagrama formado nessa figura
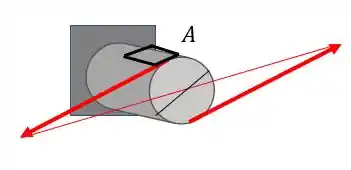
Logo a representação no nosso elemento será
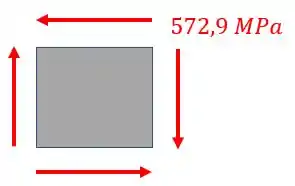
Passo 6
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.
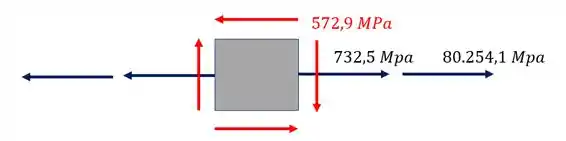
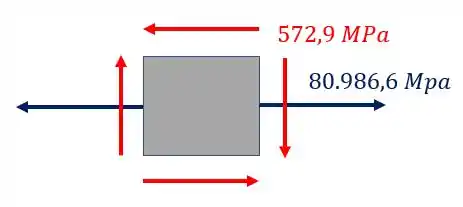
Resposta
Exercício Resolvido #8
Elaboração própria
A barra de aço retangular abaixo, de base 30mm e altura 70mm, foi sujeita ao carregamento mostrado na figura. Determine o estado plano de tensões que ocorrem no ponto B da nossa barra.
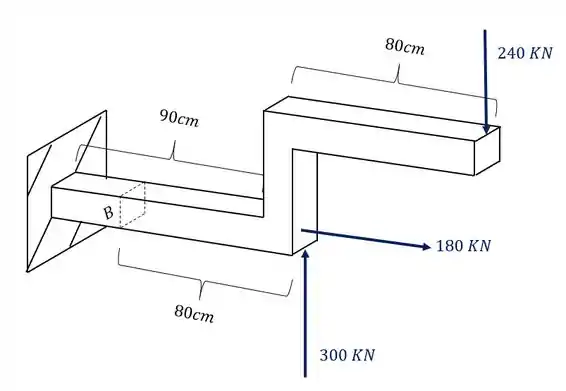
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto B.
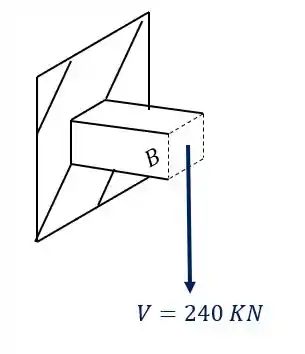
Analisando primeiro a carga de 240KN que vemos que ela produz uma força cortante, também um esforço fletor como mostra a figura abaixo.
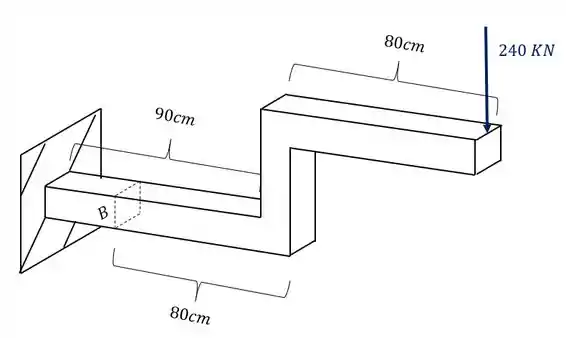
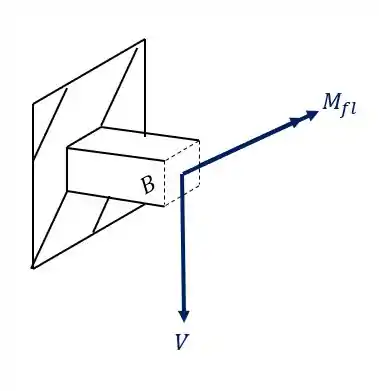
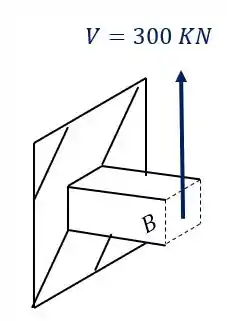
podemos ver também que a carga de 300 KN produz uma componente cortante e também um momento fletor
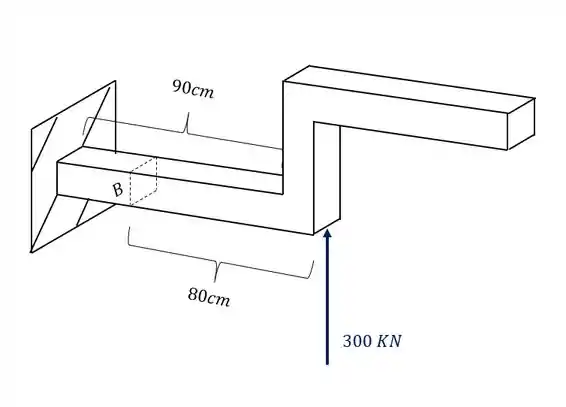
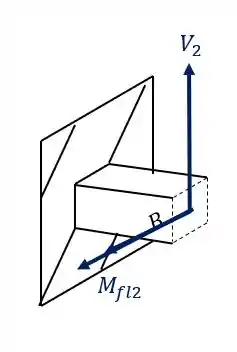
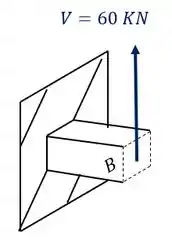
Além disso podemos ver que a carga de 180 KN produz na nossa seção apenas uma componente, que nesse caso é uma força normal, como podemos ver na nossa figura
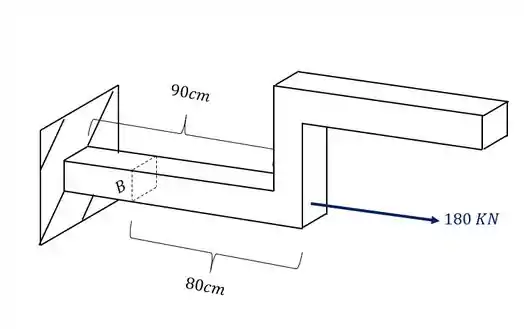
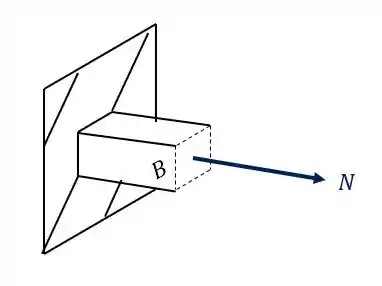
Analisando a nossa seção com todos os esforços juntos teremos que
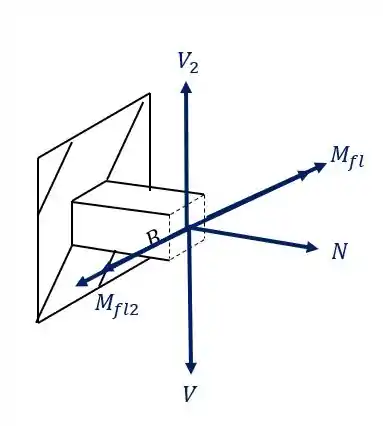
Nesse caso tanto o cortante quanto o momento fletor são diferentes, logo, precisamos usar características diferentes já que ambos os valores são diferentes.
Passo 2
Agora que já descobrimos os esforços que aparecem, precisamos calcula-los. Já sabemos de antemão que a força normal produz esforços normais, assim como o momento fletor. Da mesma forma força cortante produz esforços cisalhantes assim como o torsor. Então vamos dividir essa segunda parte da solução em duas partes.
Primeiro vamos calcular os esforços normais devido a ação da força normal.
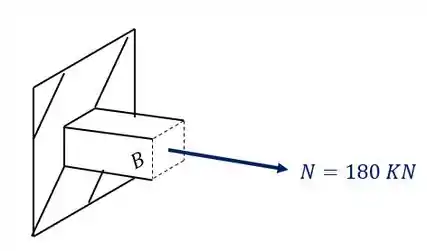
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que o normal será dado por
E a área será dada por
Substituindo na fórmula principal teremos que
Olhando novamente a figura, vemos que nosso elemento é
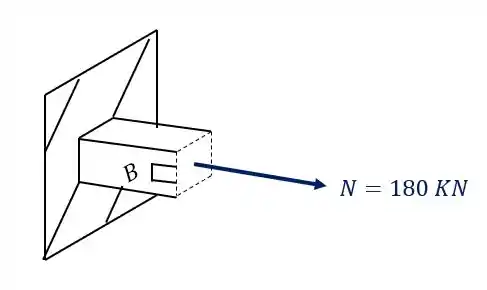
O nosso elemento isolado com a tensão será
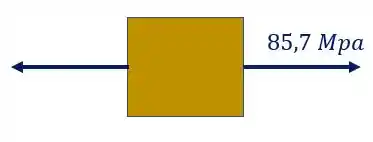
É importante perceber, que como calculamos o valor de tensão normal e ele deu positivo, significa que ele está tracionado o nosso elemento.
Passo 3
Vamos calcular os esforços normais devido a ação do momento fletor. Mas perceba o seguinte, devemos primeiro calcular o momento devido a carga de 240 KN e depois a causada pela carga de 300 KN, e fazer o cálculo para a carga resultante. Com isso teremos que, primeiro
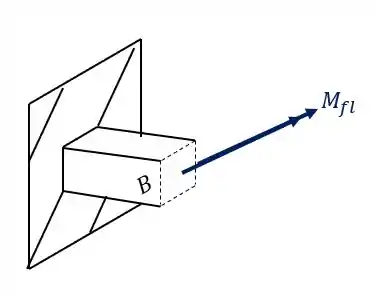
Como esse momento fletor é causado pela carga de 240 KN, devemos fazer o valor da carga vezes o braço de alavanca, com isso teremos que
Também sabemos que há um momento fletor na outra direção, que na nossa figura é dada por
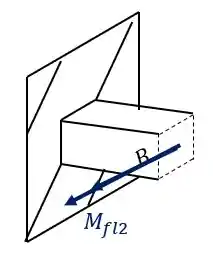
Como esse momento fletor é causado pela carga de 300 KN, devemos fazer o valor da carga vezes o braço de alavanca, com isso teremos que
Logo o nosso momento fletor resultante será
Sabemos que a fórmula que nos auxilia nesse cálculo é
Sabemos que y é a distância do centro da peça até o ponto calculado, como esse ponto está em cima da linha neutra, sabemos que seu valor é zero, logo
Se substituirmos isso na nossa equação teremos que
Ou seja, os esforços fletores não interferiram no nosso cálculo. Mas isso não significa que os esforços normais são zero, além do mais temos a carga de 180 KN que traciona a nossa seção, apenas podemos afirmar que para o ponto B a contribuição do momento fletor é zero.
Passo 4
Agora vamos fazer a análise por esforços cisalhantes.
Vamos primeiro analisar o cisalhante. Sabemos que a fórmula que nos auxilia no cálculo é a fórmula
Mas vamos olhar a nossa figura. Lembre-se que os nossos cortantes são diferentes, assim teremos que para o primeiro cortante teremos que
E para o segundo teremos que
Logo o nosso cortante resultante será
Logo o cortante que usaremos será
Também precisamos do momento estático da nossa seção, que é calculado por
Olhando a nossa seção teremos que
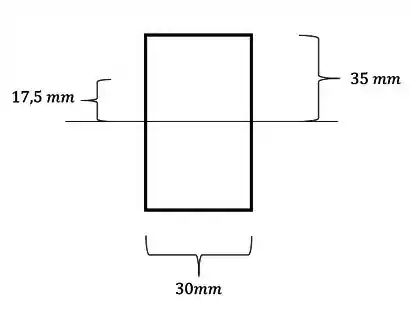
logo teremos que
Se olharmos a nossa fórmula vemos que também precisamos do valor do b, que é a espessura da nossa seção, e também já sabemos esse valor
E por fim precisamos do momento de inercia, como a seção é retangular usamos a fórmula
Como já temos as dimensões da seção, basta substituirmos esses valores
Agora que já temos os valores, basta substituirmos na nossa equação
Substituindo na nossa equação teremos que
Olhando a nossa peça teremos que
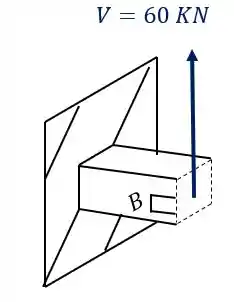
Com isso teremos que
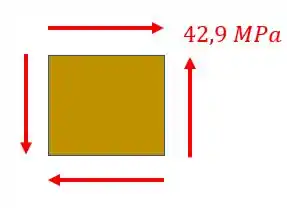
Passo 5
Por fim basta fazermos o elemento final com todos os esforços que representamos anteriormente, tendo dessa maneira o seguinte elemento para representarmos.
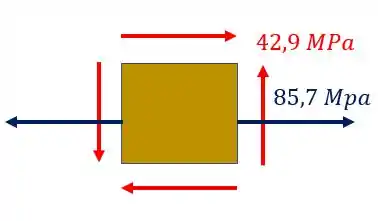
Resposta
Exercício Resolvido #9
Elaboração própria
Quais forças irão contribuir para o cálculo dos esforços que agirão na seção da nossa peça no ponto A?
Observação: não precisa calcular os valores do estado de tensões, apenas indicar os esforços.
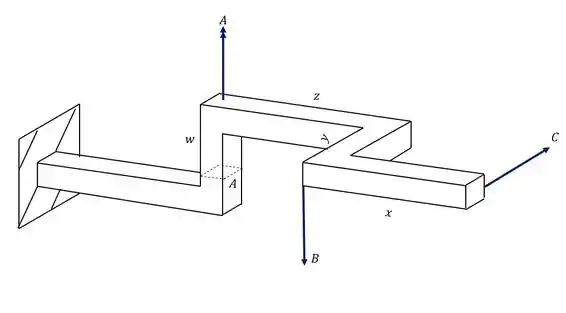
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
Analisando primeiro a carga de A vemos que ela produz uma tensão cisalhante pela ação do torsor, e sabemos que a fórmula para calcularmos a tensão em função do torsor é
Analisando a nossa seção teremos que
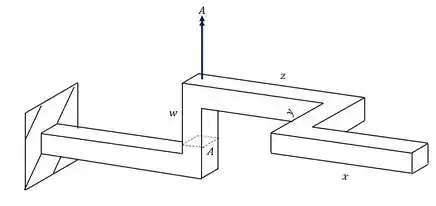
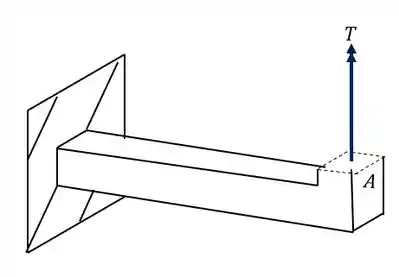
Passo 2
Analisando a carga B vemos que ela produz 3 esforços. O primeiro é o próprio esforço de compressão, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca y, e que é calculado pela fórmula
Porém também vemos que ele produz um fletor com braço de alavanca Z, e que será calculado pela fórmula
Olhando a nossa seção teremos que
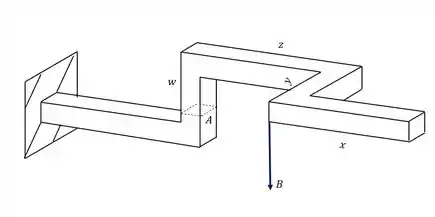
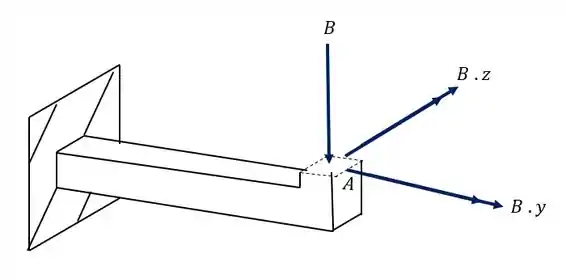
Podemos ver nesse caso que a contribuição do momento fletor será zero, exatamente pelo fato do ponto A estar bem em cima da linha neutra para ação desse momento fletor.
Passo 3
Agora só falta analisarmos o ultimo esforço, causado pela carga C. nesse caso ela produz 3 esforços.
O primeiro esforço é o esforço cortante, que usaremos para calcular a tensão cisalhante, e nesse caso usamos a fórmula
Também temos a ação do torsor em que o braço de alavanca é X+Z e sabemos que a fórmula que usamos para o calculo é
E por fim ele também produz um esforço fletor, tome cuidado para na prova não esquecer ele, pois nesse caso o braço de alavanca é a altura W, e geralmente esquecemos de calcular esse esforço por ele ser bem escondido, analisando a nossa seção teremos
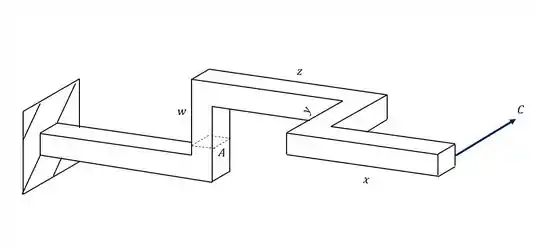
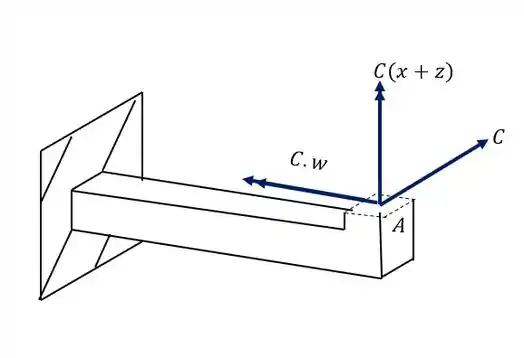
E agora analisamos a mesma questão anterior, o ponto A está exatamente em cima da linha neutra causada pelo momento fletor , ou seja, a contribuição do momento fletor nesse caso é zero.
Passo 4
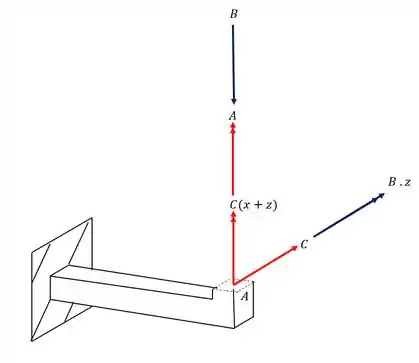
Analisando todos os esforços que agem na seção teremos que
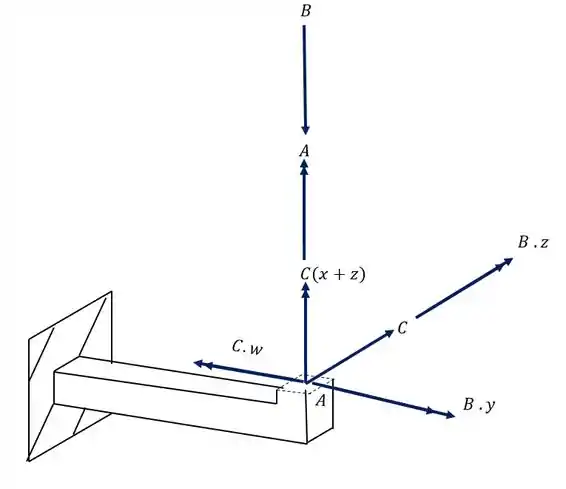
Como já vimos os momentos fletores que contem o ponto A não iram influenciar no nosso valor logo, os esforços que devemos considerar são
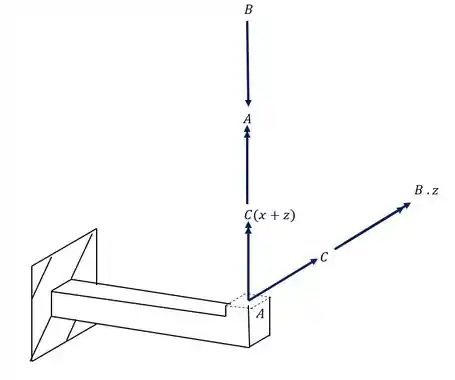
Dividindo em azul os esforços que causam tensão normal e em vermelho os esforços que causam tensão cisalhante, teremos que
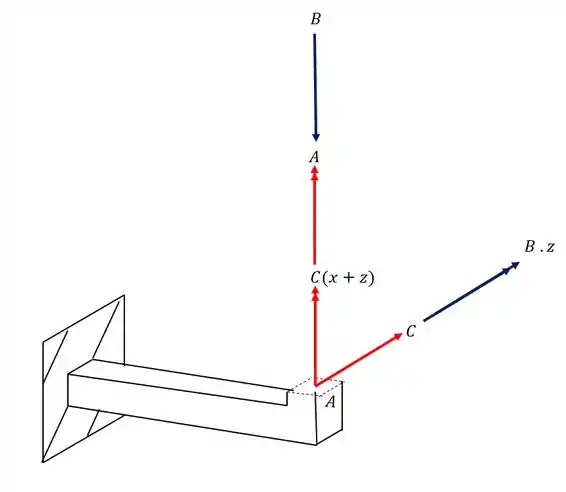
Resposta
Os esforços que contribuem são os que estão demonstrados na figura abaixo, exatamente na seção que destacamos, logo temos que:
Exercício Resolvido #10
Elaboração própria
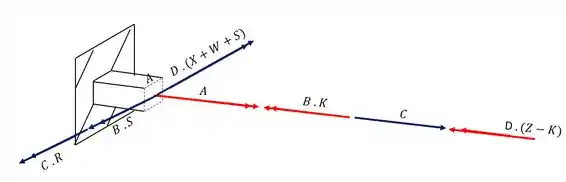
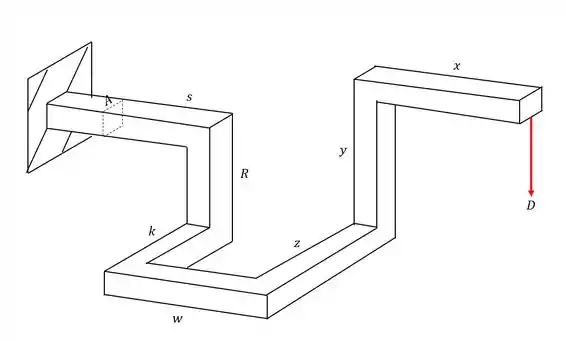
Quais forças iram contribuir para o cálculo dos esforços que agirão na seção da nossa peça no ponto A.
Observação: não precisa calcular os valores do estado de tensões, apenas indicar os esforços.
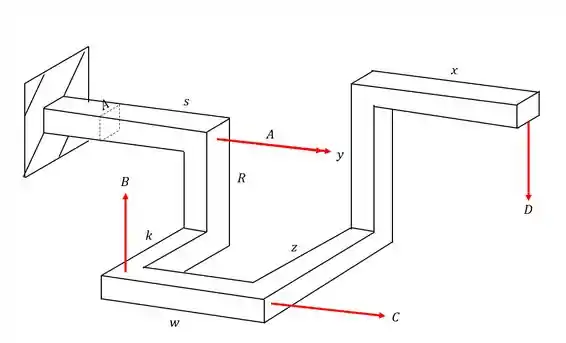
Passo 1
Para começar essa questão, devemos nos lembrar do nosso passo a passo. Devemos primeiro levar todos os esforços produzidos pelas cargas para a seção que se deseja calcular e analisar como esses esforços afetam o ponto A.
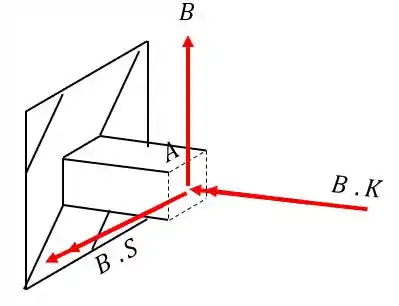
Analisando primeiro a carga de A vemos que ela produz uma tensão cisalhante pela ação do torsor, e sabemos que a fórmula para calcularmos a tensão em função do torsor é
Analisando a nossa seção teremos que
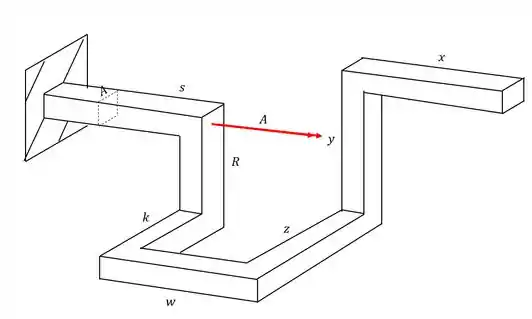
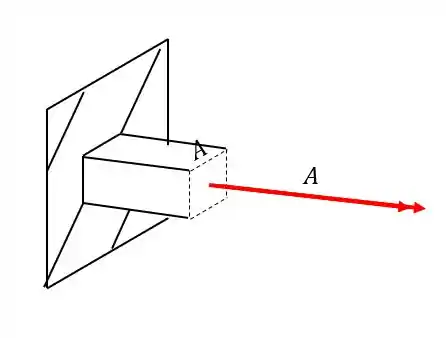
Como apenas se trata de um esforço de torção, basta que levemos diretamente para a nossa seção diretamente, sem nos preocuparmos com braços de alavanca por exemplo.
Passo 2
Analisando a carga B vemos que ela produz 3 esforços. O primeiro é o próprio esforço de cortante, que produz a tensão cisalhante, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca S, e que é calculado pela fórmula
Porém também vemos que ele produz um torsor com braço de alavanca K, e que será calculado pela fórmula
Olhando a nossa seção teremos que
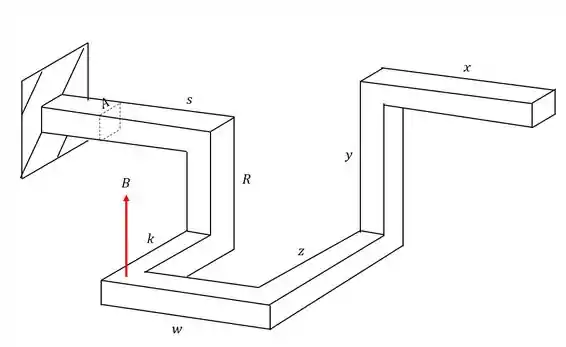
Passo 3
Analisando a carga C vemos que ela produz 3 esforços. O primeiro é o próprio esforço de tração, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca K, e que é calculado pela fórmula
Porém também vemos que ele produz um fletor com braço de alavanca R, e que será calculado pela fórmula
Olhando a nossa seção teremos que
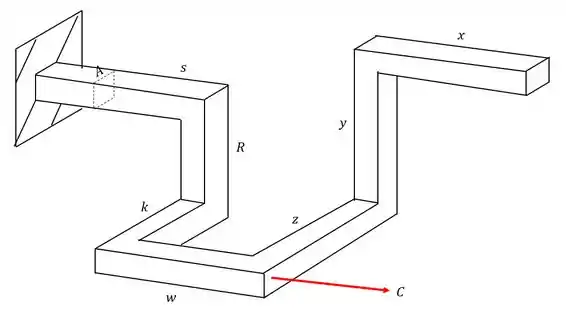
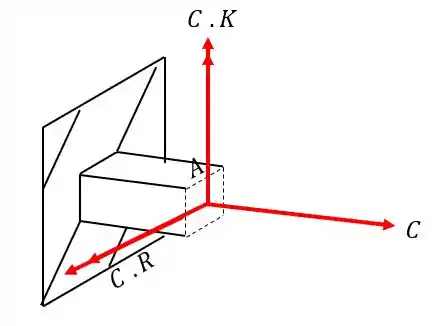
O ponto A está exatamente em cima da linha neutra causada pelo momento fletor , ou seja, a contribuição do momento fletor nesse caso é zero.
Passo 4
Analisando a carga D vemos que ela produz 3 esforços. O primeiro é o próprio esforço de cortante, que produz a tensão cisalhante, que usamos a fórmula
Também vemos que ele produz um esforço fletor, com braço de alavanca , e que é calculado pela fórmula
Porém também vemos que ele produz um torsor com braço de alavanca , e que será calculado pela fórmula
Olhando a nossa seção teremos que
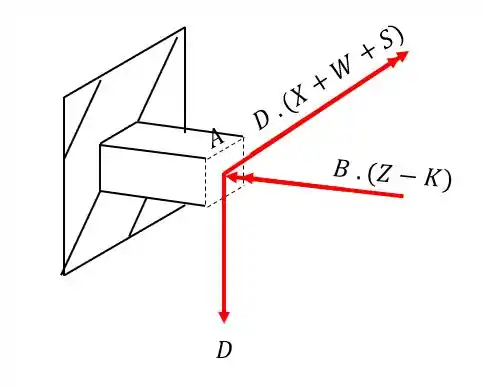
Passo 5
Analisando todos os esforços que agem na seção teremos que
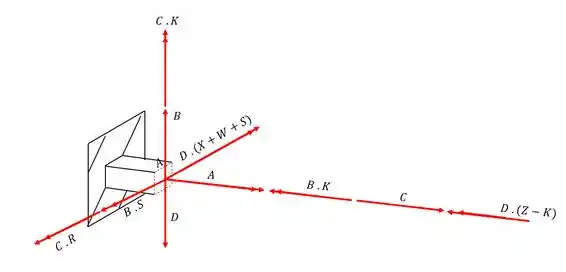
Como já vimos os momentos fletores que contém o ponto A não iram influenciar no nosso valor logo, os esforços que devemos considerar são
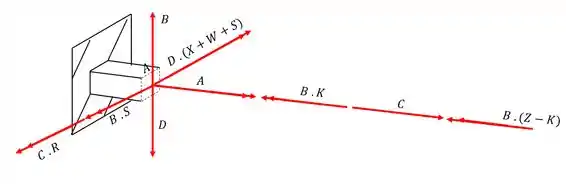
Outra coisa que podemos notar é, como o ponto A está na extremidade da seção, sabemos que o momento estático dele é zero, ou seja, a contribuição das tensões cisalhantes devido a ação do cortante também será zero, então teremos que
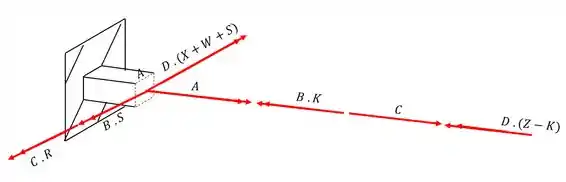
Dividindo em azul as tensões que causam esforço normal e de vermelho os esforços cisalhantes teremos que
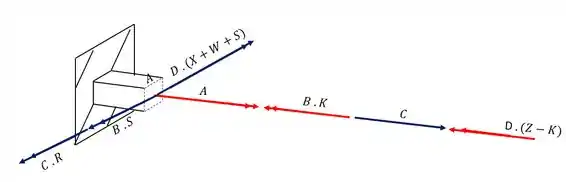
Resposta
Os esforços que contribuem são os que estão demonstrados na figura abaixo, exatamente na seção que destacamos, logo temos que