Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Subespaço Vetorial

Ver Todos os Exercícios

Teoria

Introdução

Faala aí! Vamos agora aprender um carinha para complementar nosso estudo do espaço vetorial, o Subespaço Vetorial!

Vamos começar pegando a ideia desse subespaço vetorial relembrando um pouco sobre os espaços vetoriais.

É sempre bom a gente pensar no espaço vetorial como sendo umgrande conjunto V com vários elementos que devem respeitar um conjunto de regrinhas (os axiomas dos espaços vetoriais). Tai elementos são o que chamamos de vetores. A gente pode ilustrar essa ideia com a figura abaixo:

Nesta imagem, nosso espaço vetorial é o conjunto V com os vetores u, v e o w.

Com essa ideia em mente, podemos entender o subespaço como sendo um conjunto S dentro desse espaço vetorial V (por isso dizemos que ele é um subconjunto de V ). Ele vai pegar alguns ou até mesmo todos os elementos desse espaço vetorial. Podemos ver a ideia melhor nessa imagem aqui

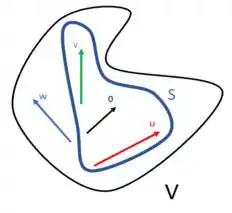
A gente ve que o subespaço vetorial S do espaço vetorial V é um conjunto que envolve os vetores u ,   v e aquele vetor 0 . Olha, eu vou admitir que eu envolvi aquele vetor 0 de propósito Lembra que o espaço vetorial tem algumas regrinhas? Então, o subespaço vetorial também possui algumas regras também e uma delas eu já te adiantei: todo subespaço vetorial deve conter o vetor nulo. Tudo bem?

Resumo: O subespaço vetorial S de um espaço vetorial V é um conjunto de elementos de V que devem respeitar algumas regras.

Regras do Subespaço Vetorial

Vamos aprender aqui as condições para que um subconjunto S de um espaço vetorial V seja um subespaço vetorial de V . Primeirou eu vou apresentar as regras de uma forma traduzida e depois eu vou mostrar como elas aparecem, tudo bem? Vamos lá:

S vai ser um subespaço vetorial de V se:

  1. O vetor nulo esteja dentro de S . Sempre devemos verificar se o vetor nulo de V está presente nesse subconjunto de S .
  2. Se somarmos dois vetores u e v que estão em S , o resultado desta soma também deve estar dentro de S ;
  3. Se multiplicarmos qualquer vetor u de S por um número α real qualquer, o resultado deste produto deve estar dentro de S .

Em geral, as regras na forma que usamos nos exercícios são as seguintes:

  1. 0   ∈ S ;
  2. Para quaisquer u e v   ∈ S , temos que u + v   ∈ S ;
  3. Para qualquer   u ∈ S e α ∈   R , temos que α . u   ∈ R   .

A vantagem dos subespaços vetoriais é que só precisamos verificar essas três regrinhas ao contrário daquelas oito que a gente tinha que verificar nos espaços vetoriais.

Vamos pegar essa ideia de subespaço vetorial com alguns exemplos!

Verificando se os subconjuntos são subespaços vetoriais

Vamos começar conferindo se o seguinte subconjunto S é um subespaço vetorial:

S = x , 0 ∈   R 2

A gente começa entendendo melhor o que esse código todo está querendo nos dizer. Bem, o enunciado nos fala que o S é um subconjunto do R 2 . Se você não lembra quem é R 2 , relaxa, ele só é o conjunto de todos os pares x , y em que esse x e esse y podem ser quaisquer números reais, ok?

Voltando ao subconjunto S , ele nos fala que ele é composto por todos os pares ( x , y ) cujo a segunda componente, ou seja, o y é igual a zero. Em resumo, é o conjunto com todos os pares da forma ( x , 0 ) .

Tá ok, mas como a gente vê se isso é um subespaço vetorial ou não? Ora, temos que investigar se eles respeitam aquelas três regrinhas que eu mostrei ali em cima.

Começamos pela primeira regra: Será que o vetor nulo de R 2 está presente em nosso subconjunto S ? Para responder isso, vamos lembrar quem é o velor nulo de R 2 . É o vetor que todas as suas componentes são nulas:

0 = ( 0,0 )

Olha, se escolhermos x = 0 nos vetores de S , teremos o vetor ( 0,0 ) que é justamente o vetor nulo de R 2 ! Primeira regra, check!

Na segunda regrinha, vamos precisar somar dois vetores de S e ver se o resultado continua sendo um vetor do tipo ( x ,   0 ) . Vamos fazer isso supondo dois vetores de S , são eles:

u = x 1 , 0 v = ( x 2 , 0 )

A soma deles é

u + v = x 1 , 0 + ( x 2 , 0 )

Para calcular essa soma, devemos somar cada elemento do parêntesis com o elemento na mesma posição do outro vetor. Fica dessa forma aqui:

u + v   = x 1 +   x 2 , 0 + 0 = ( x 1 +   x 2 , 0 )

Como x 1 e x 2 têm de ser reais, sua soma também é um número real. Então, o resultado de u + v é o vetor ( x 1 +   x 2 , 0 ) que possui a primeira componente um número real qualquer e a segunda componente é nula. Isso é exatamente a condição para um vetor estar em S como o enunciado nos disse. Então, segunda regra check!

Para verificarmos a terceira regra, precisamos supor um vetor qualquer, que eu vou usar aquele u que eu já usei para checar a segunda regra, e um número real α qualquer. Vamos realizar o seguinte produto

α .   u = α . ( x 1 ,   0 )

Para fazer esse produto, multiplicamos cada componente por α :

α .   u = α .   x 1 ,   α . 0 =   α .   x 1 ,   0

Como tanto x 1 quanto α é real, o produto α . x 1 também é um número real. Então, o produto α . u resulta no vetor ( α x 1 ,   0 ) que tem como primeira componente qualquer número real α . x 1 e a segunda componente nula. Isso é exatamente a condição para este vetor estar em S !! Terceira regra, OK!

Como todas as regras estão valendo, podemos concluir que S é um subespaço vetorial de R 2 !

Retas como subespaços vetoriais

Outro exemplo bastante comum é o seguinte. Vamos mostrar que a reta y = 2 x é um subespaço vetorial de R 2 .

Opaaa!! Esse exemplo veio um pouco diferente. Cadê o subconjunto S que a gente vem sempre vendo?

Calmaa! Existem casos em que nós vamos ter que construir o subconjunto. Este exemplo é um deles.

O exercício nos diz que estamos no R 2 , então já sabemos que o subconjunto S é uma cópia do R 2 com alguma coisa diferente. Como o R 2 é o conjunto de todos os pares x , y , como já vimos ali em cima, a única coisa que devemos fazer é trocar esse valor de y por y = 2 x como o problema nos diz! Desta forma, o nosso subconjunto S é da forma:

S = x ,   2 x   c o m   x   ∈ R

Tudo bem? Então vamos lá!

Precisamos testar a primeira regra para esse S ser um subespaço. Será que conseguimos encontrar o vetor nulo de R 2 (aquele 0 = ( 0,0 ) ) em S ? Se escolhermos x = 0 , teremos

0 ,   2.0 = 0,0

E a gente vê que se escolhermos x = 0 , temos o vetor nulo em S . Primeira regra bateu!!

Na segunda, precisamos supor dois vetore u e v pertencentes a S , eu vou escolher os seguintes vetores:

u = x 1 ,   2 . x 1 v = x 2 , 2 . x 2

Percebeu que eu tenho que supor vetores que possuam aquela estrutura de ( x , 2 x ) com x real, né? Agora, precisamos somar u e v para ver se mantemos esta estrutura:

u + v = x 1 ,   2 x 1 +   x 2 ,   2 x 2

Fazemos essa soma somando as componentes que estão nas mesmas posições nos parêntesis:

u + v = x 1 + x 2 ,   2 x 1 + 2 x 2

Olha, na segunda componente nós temos o número 2 multiplicando todos os termos. Então, podemos coloca-lo em evidência dessa forma aqui:

u + v = x 1 + x 2 ,   2 ( x 1 + x 2 )

Como x 1 e x 2 têm de ser reais, sua soma também é um número real. Então, o resultado de u + v é o vetor ( x 1 +   x 2 , 2 ( x 1 + x 2 ) ) que possui a primeira componente um número real qualquer e a segunda componente é o dobro da primeira. Isso é exatamente a condição para um vetor estar em S como o enunciado nos disse. Então, segunda regra check!

Para verificarmos a terceira regra, precisamos supor um vetor qualquer, que eu vou usar aquele u que eu já usei para checar a segunda regra, e um número real α qualquer. Vamos realizar o seguinte produto

α .   u = α . ( x 1 ,   2 x 1 )

Para fazer esse produto, multiplicamos cada componente por α :

α .   u = α .   x 1 ,   α . 2 x 1 =   α x 1 ,   2 a x 1

A gente usou aqui que a ordem dos fatores não altera o produto, então a . 2 . x 1 = 2 . a . x 1 . Como tanto x 1 quanto α é real, o produto α . x 1 também é um número real. Então, o produto α . u resulta no vetor ( α x 1 ,   2 a x 1 ) que tem como primeira componente qualquer número real α . x 1 e a segunda componente é o dobro da primeira. Isso é exatamente a condição para este vetor estar em S !! Terceira regra, OK!

Como todas as regras estão valendo, podemos concluir que S é um subespaço vetorial de R 2 !

Matrizes como subespaços vetoriais

Vamos verificar que o subconjunto S a seguir é um subespaço vetorial do Espaço vetorial das matrizes 2 × 2 .

S = 1 b c 0   ∈ M 2 R

Primeiro, vamos entender esse código estranho aí. O enunciado nos fala que S é o subconjunto de todas as matrizes 2 × 2 com elementos reais (isso que significa aquele M 2 R ) em que o elemento da primeira linha e primeira coluna é igual a 1 e o segundo número da segunda coluna tem que ser igual a zero.

Para pegar a ideia, vou mostrar algumas matrizes que podem estar nesse subconjunto S :

1 2 3 0 ;   1 5 7 0 ;   1 12 27 0 ; …

Entendido isso, vamos às nossas regrinhas! Para testarmos a primeira regra, precisamos conhecer quem é o vetor nulo no mundo das matrizes 2 × 2 .

O vetor nulo nessas matrizes é dado por uma matriz 2 × 2 com todos os elementos dela iguais a zero, dessa maneira aqui ó:

0 = 0 0 0 0

Vamos ver agora se conseguimos construir essa matriz seguindo as regras das matrizes que pertencem ao subconjunto S .

Olha só, como todas as matrizes que estão em S precisam ter o elemento da primeira linha e primeira coluna igual a 1 , a gente nunca vai conseguir zerar todos os termos das matrizes de S . Então o vetor 0 não pertence ao subconjunto S que por sua vez não é um subespaço vetorial de M 2 R . Que pena ☹

É isso, galera. O procedimento para testar se os subconjuntos dados são ou não subespaços vetoriais é sempre este. Sempre vamos ter de testar aquelas 3 regrinhas. Com a prática, você já vai ser capaz de testar direto aquelas regras que você acha que o subconjunto não respeita!!

Então... está esperando o quê para treinar nos exercícios? Estarei lá te esperando 😊

Verificando se os subconjuntos são subespaços vetoriais

Retas como subespaços vetoriais

Matrizes como subespaços vetoriais

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 2ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 86 - problema 3.1.

Determine se K é subespaço vetorial de R 3 :

c   K = a , 1,1 ∈ R 3 a ∈ R }

Passo 1

Faaaala aí! Vambora para essa questão sobre subespaço vetorial!

Um subespaço vetorial U tem que atender 3 condições!

  • 0   ϵ   U
  • U é fechado para soma: u , v   ϵ   U →   u + v   ϵ   U
  • U   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   U → λ u   ϵ   U

Passo 2

Vamos começar pela primeira condição!

Esse conjunto é especial porque ele é mais tranquilinho de ver se é um subespaço ou não “ué por que?”

Basta ver que como o conjunto é composto de elementos do tipo ( a , 1,1 ) , não conseguimos nenhum valor de a para obtermos o vetor nulo ( 0,0 , 0 ) , ou seja, o vetor nulo não pertence à K .

Como ele não possui o elemento nulo do R 3 , ele não é subespaço vetorial (pela primeira condição dos subespaços vetoriais).

Vamos continuar com nossos estudos para ficar fera!

Resposta

Não é subespaço vetorial.

Exercício Resolvido #2

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 2ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 86 - problema 3.1.

Determine se é subespaço vetorial de R 3 :

a   U = a , b , c ∈ R 3 a , c ∈ R ,   b = a + c + 1 }

Passo 1

Faaaala aí! Vambora para essa questão sobre subespaço vetorial!

Um subespaço vetorial U tem que atender 3 condições!

  • 0   ϵ   U
  • U é fechado para soma: u , v   ϵ   U →   u + v   ϵ   U
  • U   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   U → λ u   ϵ   U

Passo 2

Show de bolinhas, para testar se U é um subespaço vetorial de   R 3 , precisamos aplicar o teorema, então vamos começar pela primeira condição!

Temos que, no R 3 , o elemento nulo é o vetor ( 0,0 , 0 ) .

Aplicando na condição do conjunto

U = a , b , c ∈ R 3 a , c ∈ R ,   b = a + c + 1 }

Ou seja, temos valores a , b e c que têm que validar essa condição aqui:

b = a + c + 1

Como precisamos verificar o vetor nulo, temos que:

a , b , c = ( 0,0 , 0 )

Ou seja,

a = 0   ; b = 0   ; c = 0

Na condição do conjunto, temos que

b = a + c + 1

Substituindo os valores:

0 = 0 + 0 + 1

0 = 1  

Como sabemos que 0 não é igual a 1 , chegamos a um absurdo.

Logo, nenhum a ,   b e c para obter o elemento nulo. Então o elemento nulo não está contido nesse conjunto U e, portanto, não é um subespaço vetorial de R 3 .

Vamos continuar exercitando isso aí! Foco, fé e força galerinha!

Resposta

U não é subespaço vetorial de R 3 .

Exercício Resolvido #3

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 2ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 86 - problema 3.1.

Determine se é subespaço vetorial de R 3 :

b   V = a , b , c ∈ R 3 a , b ∈ R ,   2 a + 3 b = 5 c }

Passo 1

Opa, tudo certinho? Vamo que vamo para mais uma questão sobre subespaços vetoriais!

Para um conjunto V ser um subespaço temos 3 condições que ele deve obedecer:

  • 0   ϵ   V
  • V é fechado para soma: u , v   ϵ   V →   u + v   ϵ   V
  • V   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   V → λ u   ϵ   V

Passo 2

Olhando a primeira condição:

Temos que, no R 3 , o elemento nulo é o vetor ( 0,0 , 0 ) .

Ou seja, a , b , c = ( 0,0 , 0 )

Se igualarmos cara carinha de um lado com outro cara na mesma posição mas do outro lado da igualdade, temos que a = b = c = 0 .

A condição do conjunto V diz que:

2 a + 3 b = 5 c

Agora vamos substituir os valores que obtemos para a ,   b   e c :

2 ∙ 0 + 3 ∙ 0 = 5 ∙ 0

0 = 0

Como chegamos a um resultado consistente, o ( 0,0 , 0 ) pertence ao conjunto.

Show, primeira condição check!

Passo 3

Mas, calma, isso ainda não prova nada... Vamos para a segunda condição do teorema. Conjunto fechado para soma

Vamos pensar em dois vetores, v 1 e v 2 , desse jeitinho:

v 1 = a 1 , b 1 , c 1 ,   v 2 = a 2 , b 2 , c 2

E queremos analisar isso daqui:

v 1 , v 2 ∈ V ⇒ v 1 + v 2 ∈ V ?

Somando os vetores, temos que:

v 1 + v 2 = ( a 1 + a 2 , b 1 + b 2 , c 1 + c 2 )

Agora vem a sacada, onde tem a na restrição de V :

2 a + 3 b = 5 c

vamos substituir por a 1 + a 2 e a mesma coisa para b e c . Ficamos, então, com:

2 a 1 + a 2 + 3 b 1 + b 2 = 5 c 1 + c 2

Podemos ajeitar para ficarmos desse jeitinho aqui:

2 a 1 + 3 b 1 + 2 a 2 + 3 b 2 = 5 c 1 + c 2

Repare que na nossa implicação no começo do enunciado, usamos a hipótese de: v 1 , v 2 ∈ V .

Isso siginifca que eles pertencem ao conjunto e, portanto, cada uma das suas coordenadas satisfaz a equação descrita. Assim, aplicando a hipótese, temos que que:

2 a 1 + 3 b 1 = 5 c 1

E

2 a 2 + 3 b 2 = 5 c 2

Somando estas duas condições a gente tem:

2 a 1 + 3 b 1 + 2 a 2 + 3 b 2 = 5 c 1 + c 2

Que é exatamente a expressão que obtemos ali em cima!

Ou seja:

v 1 + v 2 ∈ V

Show, é verdade isso daí 😊

E assim está fechado para soma.

Uhul, segunda condição check!

Passo 4

Última condição do teorema é ser fechado para multiplicação escalar

λ ∈ R ,   v = a , b , c ∈ V ⇒ λ v ∈ V ?

Temos que o vetor multiplicado pelo escalar é

λ v = λ a , b , c

Podemos fazer como uma distributiva, ficando com

λ v =   ( λ a , λ b , λ c )

Logo, aplicando a condição do conjunto ficaríamos com:

2 λ a + 3 λ b = 5 λ c

Podemos colocar o λ em evidencia:

λ 2 a + 3 b = λ ( 5 c )

Olha só aquele parêntesis do lado esquerdo da igualdade. Como v = a , b , c ∈ V , temos a seguinte relação entre o   a ,   b e c :

( 2 a + 3 b ) = 5 c

Substituindo esse resultado na expressão de cima

λ 5 c = λ ( 5 c )

E vemos que o conjunto V é fechado para multiplicação por escalar.

Ebaa, terceira condição check!

Fechamos todas as condições, então V é um subespaço vetorial!

Resposta

V é subespaço vetorial de R 3 .

Exercício Resolvido #4

Avaliação Álgebra Linear I – EE Professora Francisca Pinto Fernandes Rosa

Às vezes é necessário detectar, dentro de um espaço vetorial V , subconjuntos S que sejam eles próprios espaços vetoriais “menores”. Tais conjuntos serão chamados subespaços vetoriais de V .

Qual das opções contém um subconjunto de R 3 que não é um subespaço vetorial?

I )   W = { a , a , 2 a , a   ϵ   R }

I I )   W = { ( 0,0 , a ) , a   ϵ   R }

I I I )   W = { ( 0,1 , a ) , a   ϵ   R }

I V ) W = { ( a , 2 a , 3 a ) , a   ϵ   R }

Passo 1

Faaaala aí! Tudo certinho? Vamos pra cima dessa questão sobre Subespaços Vetoriais!

Para um subconjunto U ser um subespaço vetorial, precisamos atender 3 condições do teorema:

  • 0   ϵ   U
  • U é fechado para soma: u , v   ϵ   U →   u + v   ϵ   U
  • U   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   U → λ u   ϵ   U

Passo 2

O que a gente vai fazer é ver qual não vai atender às condições, vamos começar fazendo a primeira condição para cada alternativa

I )   W = { a , a , 2 a , a   ϵ   R }

Temos que, no R 3 , o elemento nulo é o vetor ( 0,0 , 0 ) .

Aplicando na condição do conjunto

W = a , a , 2 a , a   ϵ   R

Ou seja,

( a , a ,   2 a ) = ( 0 , 0,0 )

Aqui a gente vê que se o a for igual a zero ficamos com:

( 0,0 , 2 ⋅ 0 )

Que dá

0,0 , 0

Show 0   ϵ   W

Passo 3

Vamos ver essa condição para as próximas opções

I I )   W = { ( 0,0 , a ) , a   ϵ   R }

Aplicando na condição do conjunto

W = 0,0 , a , a   ϵ   R

Ou seja, temos o valor

a = 0

Que, substituindo no vetor, ficamos com:

( 0,0 , 0 )

Show 0   ϵ   W aqui também

Passo 4

I I I )   W = { ( 0,1 , a ) , a   ϵ   R }

Aplicando na condição do conjunto

W = 0,1 , a , a   ϵ   R

Ou seja, temos valor

a = 0

Que, substituindo no vetor, ficamos com:

( 0,1 , 0 )

Vixiii, não tem nenhum valor de a que faça com que esse 1 vire 0 , então achamos o nosso subconjunto que não é subespaço vetorial

Resposta

I I I )   não é subespaço vetorial

Exercício Resolvido #5

Complemento Álgebra Linear – UNIP

S = { x , 0,0   ϵ   R 3 } é subespaço do R 3 ?

Passo 1

Faaaaala aí pessoal! Vamos para mais uma questão sobre subespaços vetoriais!

Bom, o enunciado pergunta se

( x , 0,0 ) é subespaço de R 3

E um subespaço vetorial S tem que atender 3 condições:

  • 0   ϵ   S
  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S
  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

    • Vamos analisar essas condições!

    Passo 2

    A primeira diz que

    • 0   ϵ   S

    como S tem que ser subespaço de R 3 , então

    0 → ( 0,0 , 0 )

    Vamos ver aqui, se fizermos

    x = 0

    Nosso vetor é

    x ,   0 ,   0 = 0,0 , 0

    Então existe um possível x em que o vetor nulo pertença ao S . A primeira condição está show de bola!

    Passo 3

    Agora vamos para a segunda!

  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S

    • Então vamos escolher dois vetores que são da forma ( x , 0,0 )

    u = ( a , 0,0 ) v = ( b , 0,0 )

    Agora vamos somar esses vetores

    u + v = a , 0,0 + b , 0,0 = a + b , 0,0

    Isso continua na forma de S pois as duas últimas coordenadas ainda são zero!

    Show, fechou essa condição também!

    Passo 4

    Bora para terceira e última condição

  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

Vamos usar o mesmo vetor u = a , 0,0

Multiplicando-o por um escalar λ , temos que

λ ⋅ u = λ a , 0,0

Isso nos dá que

λ ⋅ u = λ a , λ . 0 , λ . 0 = ( λ a ,   0 ,   0 )

Continuou dentro do formato! Então essa condição também foi atendida

Show, atendemos as três condições, então podemos dizer que sim, S = { x , 0,0   ϵ   R 3 } é subespaço do R 3

Resposta

S = { x , 0,0   ϵ   R 3 } é subespaço vetorial do R 3

Exercício Resolvido #6

Álgebra Linear – notas de aula Sérgio Luís Zani

Verifique se S = { x , y , z ϵ   R 3 ; x + y + z = 0 } é subespaço vetorial de R 3

Passo 1

Opa fala aí! Vamo que vamo para mais uma questão sobre subespaços vetoriais!

Bom, o enunciado pergunta se

( x , y , z ) com a restrição de x + y + z = 0   é subespaço de R 3

E um subespaço vetorial S tem que atender 3 condições:

  • 0   ϵ   S
  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S
  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

    • Vamos analisar essas condições!

    Passo 2

    A primeira diz que

    • 0   ϵ   S

    e como o S tem que ser subespaço de R 3 , então, o vetor nulo tem que ter essa carinha aqui:

    0 → ( 0,0 , 0 )

    Nosso vetorzinho é

    ( x , y , z )

    Vamos ver aqui, para chegar no vetor nulo que eu já mostrei a gente pode fazer x = 0 ,   y = 0 e z = 0  

    Temos

    ( 0,0 , 0 )

    Mas a gente ainda tem que ver se a restrição do enunciado bate

    x + y + z = 0

    Substituindo os valores, temos que

    0 + 0 + 0 = 0

    0 = 0

    Isso é verdade, então show! Nossa primeira condição está check!

    Passo 3

    Agora vamos para a segunda!

  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S

    • Vamos escolher dois vetores para ver nossa condição

    u = ( a , b , c ) e v = ( u , v , w )

    Agora vamos fazer u + v

    u + v = a , b , c + u + v + w

    Juntando isso daí, temos:

    u + v = a + u , b + v , c + w

    Agora vamos colocar isso na nossa restrição!

    Nosso x = a + u , nosso y = b + v e nosso z = c + w e a nossa restrição nos diz que devemos ter

    x + y + z = 0

    Substituindo temos:

    a + u + b + v + c + w = 0

    Agora vamos separar isso desse jeitinho aqui

    a + b + c + u + v + w = 0

    Como ( a , b , c ) está incluso em S , a soma de a + b + c tem que ser igual a zero, mesma coisa para u + v + w

    Então, temos que

    0 + 0 = 0

    0 = 0

    Beleza, então segunda condição cheeeck!

    Passo 4

    Bora para terceira e última condição

  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

A gente tem que pegar um escalar (que vamos chamar de λ )   e multiplicar pelo nosso vetor

λ ⋅ x , y , z = ( λ x , λ y , λ z )

Agora colocando isso na nossa restrição, temos

λ x + λ y + λ z = 0

Podemos colocar o λ em evidência, ficando com

λ ⋅ x + y + z = 0

E como temos, pela restrição que x + y + z = 0 , ficamos com

λ ⋅ 0 = 0

0 = 0

Uhul, fechamos as 3 condições então!

S = { x , y , z ϵ   R 3 ; x + y + z = 0 } é subespaço vetorial de R 3

Resposta

S = { x , y , z ϵ   R 3 ; x + y + z = 0 } é subespaço vetorial de R 3

Exercício Resolvido #7

Complementos de Álgebra Linear – UNIP

Sendo M = { ( 1,0 , 1 ) , ( 0,0 , 1 ) } ⊂ R 3   determinar o subespaço gerado por M

Passo 1

Faaaaala aí!! Simbora para mais uma questão sobre subespaços vetoriais!

Essa questão é um pouquinho diferente, ao invés de perguntar se uma combinação é um subespaço a questão pede para a gente o próprio subespaço.

Bom, um subespaço é gerado por uma combinação, nesse caso desses vetores ( 1,0 , 1 ) e ( 0,0 , 1 ) , fazendo uma combinação a partir de operações de soma e multiplicação:

a 1,01 + b ( 0,0 , 1 )

Passo 2

Então temos isso daqui:

x , y , z = a 1,0 , 1 + b ( 0,0 , 1 )

Vamos fazer a distributiva!

x , y , z = a , 0 , a + 0,0 , b

Somando as coordenadas desses dois vetores, temos

x , y , z = a , 0 , a + b

Passo 3

Show, agora escrevendo isso bonitinho, temos que

M = { x , y , z ϵ   R 3 | x , y , z = a 1,0 , 1 + b ( 0,0 , 1 ) }

Ou seja,

M = { a , 0 , a + b   ϵ   R 3 }

Resposta

M = { a , 0 , a + b   ϵ   R 3 }

Exercício Resolvido #8

Complemento de Álgebra Linear – UNIP

R = x , y , z   ϵ   R 3 x = 0   e   y = z }   é subespaço do R 3 ?

Passo 1

Opa, tudo certo? Bora para mais uma questão sobre subespaço vetorial

O enunciado quer saber se R é subespaço de R 3

Mas esse enunciado está diferente né? Vamos achar como podemos escrever essa condição como um vetor.

Temos que um vetor do R 3 nesse conjunto pode ser escrito como

x , y , z

Em que devemos ter x = 0 e y = z conforme as condições que o exercício nos dá.

Então podemos escrever desse jeitão aqui

0 , y , y

Beleza?

Passo 2

Show, agora vamos relembrar as condições para R ser um subespaço vetorial:

  • 0   ϵ   R
  • R é fechado para soma: u , v   ϵ   R →   u + v   ϵ   R
  • R   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   R → λ u   ϵ   R

    • Vamos analisar essas condições!

    Passo 3

    A primeira diz que

    • 0   ϵ   R

    e nosso R está em R 3 , então o vetor nulo é o vetor nulo do R 3

    0 → ( 0,0 , 0 )

    Lembrando a cara do vetor em R

    ( 0 , y , y )

    Vamos ver se existe algum y para termos

    ( 0 , y , y ) = ( 0 , 0,0 )

    Daí vemos que dá para fazer y = 0 e a gente chega no vetor nulo. Então a primeira condição está show de bola!

    Passo 4

    Simbora para a segunda!

  • R é fechado para soma: u , v   ϵ   R →   u + v   ϵ   R

    • Então vamos escolher dois vetores que são da forma ( 0 , y , y )

    u = ( 0 , a , a ) v = ( 0 , b , b )

    Agora vamos somar esses vetores

    u + v = 0 , a , a + 0 , b , b = 0 , a + b , a + b

    Isso continua na forma de S pois a primeira coordenada ainda é zero, ou seja, ainda temos algo do tipo ( 0 , y , y ) !

    Show, fechou essa condição também!

    Passo 5

    Vamos finalmente para terceira condição

  • R   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   R → λ u   ϵ   R

Vamos usar o mesmo vetor u = 0 , a , a

Multiplicando-o por um escalar λ , temos que

λ ⋅ u = λ 0 , a , a

Isso nos dá que

λ ⋅ u = 0 , λ a , λ a

Continuou dentro do formato! Então essa condição também foi atendida

Show, atendemos as três condições, então podemos dizer que sim, R = { x , 0,0   ϵ   R 3 } é subespaço do R 3

Resposta

R = x , y , z   ϵ   R 3 x = 0   e   y = z }   é subespaço do R 3

Exercício Resolvido #9

Complementos de Álgebra Linear – UNIP

S = 1 b c 0   ϵ   M 2 R é subespaço de M 2 ( R ) ?

Passo 1

Faaaala aí! Vamos para mais uma questão sobre subespaços vetoriais!

Epa para tudo, tem uma matriz aí, pode isso? Pode sim hehe. Isso não vai mudar muita coisa nas nossas condições para S ser um subespaço vetorial. Vamos lembrar quem são as condições?

  • 0   ϵ   S
  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S
  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

    • A única diferença é que estamos falando de uma matriz, mas a ideia é a mesma.

    Só uma última coisinha antes de partirmos para testar essas condições:

    Esse M 2 ( R ) que aparece no enunciado é o conjunto de todas as matrizes 2 × 2 com os elementos reais. Ou seja, qualquer matriz com essa cara aqui:

    a b c d

    Prontinho! Estamos com tudo em mãos para resolver essa questão!

    Passo 2

    Vamos começar analisando a primeira condição

  • 0   ϵ   S

Como estamos no conjunto de matrizes 2 × 2 , o vetor nulo tem que ser uma matriz 2 × 2 com todos os elementos nulos:

0 0 0 0

Vamos ter que considerar uma matriz do conjunto S que tem que ter essa carinha aqui

1 b c 0

E ver se conseguimos achar um b e um c que faça com que essa matriz seja a matriz nula. Ou seja:

1 b c 0 =   0 0 0 0

Para duas matrizes serem iguais, cada elemento de uma tem que ser igual ao elemento de mesma posição da outra matriz. Olhando as duas a gente vai ter:

1 = 0 b = 0 c = 0 0 =   0

OPA!!! 1 = 0?! A gente se deparou com uma impossibilidade, não tem nenhum b nem c que faça com que 1 seja igual a 0. Então não tem jeito de existir uma matriz dentro do conjunto S que seja a matriz nula ☹

Como S já não segue a primeira condição, podemos afirmar que S não é subespaço de M 2 R

Nem precisamos ver as outras condições porque a primeira já veta a possibilidade de ser subespaço!

Resposta

S = 1 b c 0   ϵ   M 2 R não é subespaço de M 2 R

Exercício Resolvido #10

Complementos de Álgebra Linear – UNIP

S = a b c 0   ϵ   M 2 R é subespaço de M 2 ( R ) ?

Passo 1

Faaaala aí! Vamos para mais uma questão sobre subespaços vetoriais!

Epa para tudo, tem uma matriz aí, pode isso? Pode sim hehe. Isso não vai mudar muita coisa nas nossas condições para S ser um subespaço vetorial. Vamos lembrar quem são as condições?

  • 0   ϵ   S
  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S
  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

    • A única diferença é que estamos falando de uma matriz, mas a ideia é a mesma

    Só uma última coisinha antes de partirmos para testar essas condições:

    Esse M 2 ( R ) que aparece no enunciado é o conjunto de todas as matrizes 2 × 2 com os elementos reais. Ou seja, qualquer matriz com essa cara aqui:

    a b c d

    Prontinho, estamos com tudo em mãos para resolver essa questão!

    Passo 2

    Vamos começar analisando a primeira condição

  • 0   ϵ   S

    • Como estamos no conjunto de matrizes 2 × 2 , o vetor nulo tem que ser uma matriz 2 × 2 com todos os elementos nulos:

    0 0 0 0

    Então vamos ver a nossa matriz que está em S , ou seja, qualquer matriz que tenha o elemento a 22 = 0 :

    a b c 0

    Se chamarmos a , b e c de zero vamos ter que

    0 0 0 0

    Show, então a gente consegue ter uma escolha de a ,   b e c que nos leva à matriz nula!

    Primeira condição check!

    Passo 3

    Vamos agora para a segunda condição

  • S é fechado para soma: u , v   ϵ   S →   u + v   ϵ   S

    • Vamos escolher duas matrizes que estejam no molde a b c 0   eu escolhi essas duas aqui:

    u =   x y z 0 v =   p q r 0

    Agora vamos somar essas matrizes. Não lembra como soma matrizes? A gente tem que somar os elementos que estão na mesma posição das duas matrizes:

    x y z 0 + p q r 0 = x + p y + q z + r 0

    E essa matriz, continua no padrão de S , com a 22 = 0 então

    u + v   ϵ   S

    Passo 4

    Agora para última condição, temos que:

  • S   é fechado para multiplicação por escalar: λ   ϵ   R   ,     u   ϵ   S → λ u   ϵ   S

Vamos usar a matriz u que criamos para ver o passo anterior

u = x y z 0

E vamos multiplicá-la por um escalar λ

λ ⋅ u = λ x y z 0

Fazendo essa multiplicação, temos

λ ⋅ u = λ x λ y λ z 0

Isso continua no molde de S , então atendemos as 3 condições do teorema.

Portanto S = a b c 0   ϵ   M 2 R é subespaço vetorial de M 2 ( R )

Resposta

S = a b c 0   ϵ   M 2 R é subespaço vetorial de M 2 R

Exercícios de Livros Relacionados

Encontrar uma base e uma dimensão do espaço-solução do sistema: x - 2 y - z = 0 2 x + y + 3 z = 0 x + 3 y + 4 z = 0
Verificar se o vetor v = ( - 1 ,- 3 ,2 ,0 ) pertence ao subespaço do R 4 gerado pelos vetores v 1 = ( 2 ,- 1 ,3 ,0 ) , v 2 = ( 1 ,0 ,1 ,0 ) e v 3 = ( 0 ,1 ,- 1 ,0 ) .