Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 13
Dado o triângulo , sejam o ponto que divide na razão e o ponto que divide na razão 3.
- Exprima e em função de , .
- Prove que as retas CX e AY são concorrentes e exprima o ponto de concorrência P em função de .
Passo 1
Facilita bastante nos fazermos um simples esboço destes pontos e destas relações para questões deste tipo. Portanto, vamos ter uma ideia do que está ocorrendo:
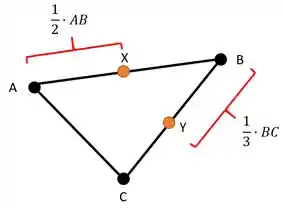
Esse simples esboço é o suficiente para nos ajudar a montar as nossas relações! Vamos começar respondendo a letra a). Para isto, vamos exprimir e em função de e .
A dica, para isto, é ir somando vetores, tentando sempre escrever em função de e , até obtemos o resultado que desejamos. Portanto,
Percebam que já conseguimos fazer aparecer um . O foco agora é transformar em uma soma de e . Para isto, sabemos que:
Portanto, o vetor é dado por:
Pronto, agora é repetir o procedimento para o vetor ! Portanto,
Percebam que já conseguimos fazer aparecer um . O foco agora é transformar em uma soma de e . Para isto, sabemos que:
Portanto, temos:
Ainda não resolvemos o nosso problema. Temos que escrever em função de e . Portanto, percebam que:
Portanto,
E assim finalizamos a letra a)!
Passo 2
Agora, vamos resolver a letra b).
Explicar que as retas CX e AY são simples. Primeiro, basta verificar que os vetores diretores destas retas não são paralelos, pois não existe pertencente aos reais tais que:
Além disto, estamos no mesmo plano! Portanto, automaticamente, temos duas retas concorrentes!
OBS: retas concorrentes são retas que se cruzam em um único ponto (pertencem a um mesmo plano e vetores diretores não são paralelos).
Continuando, vamos expressa o ponto de concorrência P em função de . Novamente, vamos fazer um desenho para nos auxiliar.
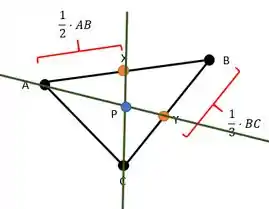
Então, vamos obter o ponto . Sabemos que ele é resultado da soma de um ponto com um vetor. Portanto,
Passo 3
E quem é ? Nosso trabalho agora é determina-lo. Para isto, vamos fazer o mesmo procedimento que fizemos no Passo 1. Portanto,
Sabemos que este vetor é proporcional a . Portanto,
Mas também sabemos que
E que . Portanto,
Só que como calculamos os vetores e no passo anterior, vamos substituir as suas relações aqui e desenvolver a equação. Portanto,
Como ambos os vetores não são paralelos, então os coeficientes que o multiplicam são, necessariamente, iguais a zero. Portanto, temos o seguinte sistema:
Resolvendo este sistema, obtemos que:
Agora, só substituir algum desses coeficientes nas nossas relações e assim obter a resposta. Portanto:
E o ponto é expresso por:
Resposta
- A
- As retas são concorrentes pois não existe pertencente aos reais tais que e também estão no mesmo plano.
O ponto é expresso por: