Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 1d

(d) D ^2^() − DE

Passo 1

Para resolvermos essa questão vamos primeiramente fazer D ^2^() que é a mesma coisa que fazer D * D. Para fazermos a multiplicação de matrizes, devemos multiplicar a linha da primeira matriz pela coluna da segunda matriz.

Temos então que:

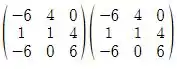
D ^2^() =

Fazendo a multiplicação temos:

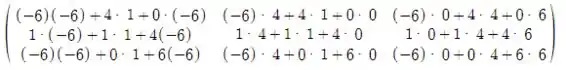
D ^2^() =

Simplificando temos:

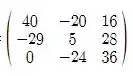
D ^2^() =

Passo 2

Agora devemos fazer a multiplicação de D*E:

Vamos fazer a mesma coisa, multiplicar as linhas da primeira matriz pelas colunas da segunda matriz.

Temos então:

D*E =

Fazendo a multiplicação, temos:

D*E =

Simplificando temos:

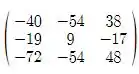
D*E =

Passo 3

Agora que temos as duas matrizes prontas podemos fazer a subtração delas, D ^2^() - D*E:

Vamos ter então;

D ^2^() - D*E =

Fazendo a subtração deles temos:

Para fazer a subtração basta você subtrair os elementos nas posições equivalentes;

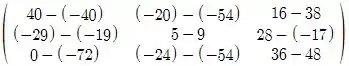
D ^2^() - D*E =

Simplificando temos:

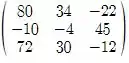
D ^2^() - D*E =

E assim terminamos essa questão !!!

Vamos para proxima ??

Resposta

D ^2^() - D*E =

Exercícios de Livros Relacionados

Dizemos que uma matriz A , nxn , é simétrica se A t = A e é anti-simétrica se A t = - A . (c)Mostre que se A e B são simétricas, então A B é simétrica se, e somente se, A B = B A
Se A B = 0 , então B A = 0 ? Justifique.
Sejam A , B e C matrizes n x n . (a)(A + B)^2 = A^2 + 2 A B + B^2 ? E se A B = B A ? Justifique.
Dizemos que uma matriz A , nxn , é simétrica se A t = A e é anti-simétrica se A t = - A . (d)Mostre que se A e B são anti-simétricas, então A + B e α A são anti-simétricas se, para todo escalar α .
Seja A uma matriz mxn e X = x 1 ⋮ x n uma matriz nx1 . Prove que A X = ∑ j = 1 n x j A j , em que A j é a j -ésima coluna de A . (Sugestão: Desenvolva o lado direito e chegue ao lado esquerdo.)