Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 4.2 - Ex. 3
Seja π1 o plano que passa pelos pontos A = (1, 1, 1), B = (1, 0, 1), C = (1, 1, 0) e π2 o plano que passa pelos pontos P = (0, 0, 1) e Q = (0, 0, 0) é paralelo ao vetor ́ i +j. Ache o ângulo entre π1 e π2.
Passo 1
Bem galera, vamos resolver essa questão aos poucos, temos então:
Seja , um plano que passa pelos pontos A(1,1,1), B(1,0,1) e C(1,1,0);
Com isso podemos concluir que AB e AC são vetores pertencentes ao plano.
Ou seja:
AB = B - A
AB = (0,-1,0)
AC = C - A
AC = (0,0-1)
Passo 2
Agora, devemos fazer o produto vetorial;
Temos: (-j)X(-k) = +i
Com isso vamos encontrar o vetor normal ao plano = (1,0,0)
Vamos utilizar o vetor normal para encontrar o ângulo entre os planos.
Seja ² o plano que passa pelos pontos P ( 0,0,1) e Q (0,0,0) e é paralelo ao vetor i+j tal que ele passa pelo plano PQ
Temo então que o plano é paralelo ao vetor i+j;
Passo 3
Agora precisamos analisar o seguinte: se o vetor i+j é paralelo ao plano, isso significa que ele também é paralelo ao ponto PQ e ao fazer o produto vetorial de PQ e i+j encontraremos o vetor normal.
Encontramos agora o vetor normal ao plano 2.
Passo 4
Agora com tudo que temos, podemos achar o ângulo entre ¹ e ².
Vamos encontrar o ângulo a partir dessa fórmula;
Sabendo que:
Vamos fazer o produto escalar entre ele:
Agora por fim, calcular o ângulo entre os vetore:
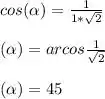
Resposta
O ângulo entre os dois planos é de 45°.