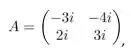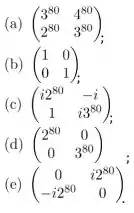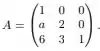Exercícios de Operações com Matrizes - Lista de Exercícios Resolvida

Determine os valores de , , e :

Seja e , calcule .

Dadas as matrizes e , calcular .

Dadas as matrizes:

Calcule:

a)

b)

c)

Dadas as matrizes:

Sabendo que e , dê as matrizes e .

Escreva a matriz coluna do tipo tal que .

Seja Se , então .

Existe apenas uma ordem de se fazer o produto das matrizes abaixo:

Descubra qual a ordem dos fatores, multiplique-os e assinale o resultado correto:

Dizemos que a matriz é antissimétrica se e simétrica se .

Assinale a alternativa FALSA:

Se é antissimétrica e diagonal então é a matriz nula

Se é antissimétrica e triangular então é a matriz nula

Se é simétrica e antissimétrica então é a matriz nula

Se é simétrica e triangular então é a matriz nula

Q3: Seja A uma matriz tal que. Podemos afirmar que o se guinte vetor é uma solução de .

(A)

(B)

(C)

(D)

Considere as matrizes

Determine tal que

O valor da entrada de é:

(A)

(B)

(C)

(D)

Considere as afirmativas abaixo:

I - Se a dimensão da imagem de é menor ou igual a , então a dimensão do núcleo de é maior ou igual a .

II - Se a dimensão do núcleo de é maior ou igual a , então a dimensão da imagem de é menor ou igual a .

(A) Todas são falsas.

(B) Apenas I é verdadeira.

(C) Apenas II é verdadeira.

(D) Todas são verdadeiras.

(E) Não sei

Considere a seguinte base de , o espaço vetorial dos polinômios de grau menor ou igual a :

Assinale abaixo o polinômio p cujas coordenadas com relação à base são .

(C)

(D)

Supondo que e são matrizes e a multiplicação é possível, assinale a alternativa FALSA:

Se a primeira e terceira linha de são iguais então a primeira e terceira linha de são iguais.

Se e são matrizes triangulares inferiores o produto é uma matriz triangular inferior.

Se a primeira e terceira coluna de são iguais então a primeira e terceira coluna de são iguais.

Se a primeira e terceira linha de são iguais então a primeira e terceira linha de são iguais.

Seja uma matriz . Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo:

A primeira linha de é igual à metade da soma de todas as linhas de ;

A segunda linha de é igual à metade da diferença entre as duas últimas linhas de ;

A terceira linha de é igual à primeira linha de ;

Qual a soma de todos os elementos da matriz ?

A primeira linha da matriz M que satisfaz

é

Sejam e matrizes tais que o produto está bem definido.

Se possui uma coluna nula, então possui uma coluna nula.

Se possui uma linha nula, então possui uma linha nula.

(a) A afirmação é verdadeira e a é falsa.

(b)Ambas as afirmações são falsas.

(c) A afirmação é falsa e a é verdadeira.

(d)Ambas as afirmações são verdadeiras

Qual das matrizes abaixo pode não ser simétrica?

(a)

(b)

(c)

(d)

Os vetores u e v do formam as colunas da matriz A = [u|v]. Sabendo que

calcule .

(a) 1

(b) 5

(c) 0

(d) 2

Seja A uma matriz . Pode-se afirmar que os produtos abaixo estão bem definidos, à exceção de:

(a)

(b)

(c)

(d)

Sejam A e B matrizes reais invers ́ıveis 4 × 4 e suponha que

em que denota a transposta da matriz . Temos que igual

Assinale a alternativa correta:

Q5. Sejam um inteiro positivo, uma matriz real e uma matriz real . Considere o sistema linear , em que a matriz de incógnitas reais é . Pode-se afirmar que:

a) se o sistema possui solução, então ;

b) se o sistema não possui solução, então

c) se o sistema possui solução, então ;

d) se , então o sistema não possui solução;

e) se , então o sistema possui infinitas soluções.

Considere em um tetraedro e a base . Sejam o ponto médio do segmento , o ponto médio do segmento e o ponto do segmento tal que . Em que denota a distância entre os pontos . Temos que a soma das coordenadas do vetor na base é igual a:

Seja uma matriz . Deseja-se construir uma matriz de forma que o produto seja uma matriz satisfazendo:

1. A primeira linha de é igual à soma de todas as colunas de
2. A segunda linha de é igual à primeira linha de menos a metade da soma das duas últimas linhas de .

Qual a soma de todos os elementos da matriz ?

Calcule o resultado do produto de matrizes abaixo:

Sejam e duas matrizes. Assinale a alternativa CORRETA:

Se é matriz-linha, então é matriz-linha

Se está definido, então também está

Se é matriz-coluna, então é matriz-coluna

Se , então

Existe apenas uma forma de se fazer o produto das matrizes abaixo:

Descubra qual a ordem dos fatores, multiplique-os e assinale o resultado correto:

Seja uma matriz . Assinale a alternativa FALSA:

(a) Se as linhas da matriz são linearmente dependentes então

(b)

(c)

(d)

(e) Não sei.

Determine se as afirmações abaixo são verdadeiras ou falsas. Prove as verdadeiras e apresente um contraexemplo para as falsas.

a) é semelhante a e é semelhante a , então é semelhante a

Se

então é:

Q16. Recorde que o traço de uma matriz quadrada é definido como sendo a soma das entradas na sua diagonal principal. Se denota a matriz dada por

Então o traço de é igual a:

a) ;

b)

c) ;

d) ;

e)

Se a matriz , , satisfaz , assinale a alternativa VERDADEIRA:

A segunda coluna de é igual à segunda coluna de menos duas vezes a primeira coluna de ;

A segunda coluna de é igual à segunda coluna de menos duas vezes a primeira coluna de ;

A segunda linha de é igual a duas vezes a primeira linha de somada à segunda linha de ;

A segunda linha de é igual à segunda linha de somada a duas vezes a primeira linha de .

Q16. A soma das duas entradas na primeira coluna da matriz

É igual a:

a)

b)

c)

d)

e)

Q2. Seja uma matriz real tal que:

A soma das entradas da matriz é igual a:

a) 0;

b) 2;

c) 1;

d) -1;

e) -2;

A matriz que representa a reflexão através da reta em pode ser obtida pelo seguinte cálculo:

(Dica: será útil saber que o vetor é ortogonal à reta .)

Determine se as afirmações abaixo são verdadeiras ou falsas. Prove as verdadeiras e apresente um contraexemplo para as falsas.

b) Se e são matrizes equivalentes, então elas têm o mesmo posto.

Lembre-se que para a multiplicação da matriz por um vetor coluna vale: onde e .

Seja e tal que e e tal que .

Então para :

.

.

.

Sejam um inteiro, A uma matriz real e considere as afirmações abaixo.

(I) Seja a matriz obtida de trocando a primeira linha pela primeira coluna (mantendo inalteradas as entradas que não estão nem na primeira linha nem na primeira coluna). Vale que .

(II) Denote por a primeira, segunda e terceira linhas de , respectivamente. Se é a matriz obtida de trocando a primeira linha por , então , quaisquer que sejam .

(III) Se é uma matriz real qualquer e denota a transposta de uma matriz X, então

As afirmações verdadeiras são:

1. apenas a 2 e 3
2. apenas a 2
3. apenas a 3
4. apenas a 1 e 2
5. apenas a 1 e 3

Sejam n um inteiro positivo e matrizes reais tais que . Considere as seguintes afirmações:

(I)

(II) se é igual à matriz identidade, então

(III) se

Assinale a alternativa correta:

As afirmações verdadeiras são:

1. apenas a 2 e 3
2. apenas a 2
3. apenas a 3
4. apenas a 1 e 2
5. apenas a 1 e 3

Sejam e considere o sistema linear

nas incógnitas reais . Se esse sistema possui uma única solução, então

é igual a:

Assinale a alternativa correta:

Considere as matrizes

e seja uma matriz real tal que , em que denota a transposta da matriz . Temos que o determinante de é igual a:

Considere as afirmativas abaixo:

I - Se um sistema admite solução então o conjunto de todas as colunas da matriz aumentada do sistema é linearmente independente.

II - Se o conjunto das colunas da matriz de coeficientes

de um sistema linear é linearmente independente, então o sistema tem solução única.

(A) Apenas I é verdadeira.

(B) Apenas II é verdadeira.

(C) Todas são falsas.

(D) Todas são verdadeiras.

(E) Não sei

Sejam e duas matrizes. Diga se as afirmativas abaixo são verdadeiras ou falsas.

1. Se , então e podem ser ambas não nulas.
2. Se e , então e têm que ser matrizes quadradas.

I é falsa e II é verdadeira

Ambas são falsas

I é verdadeira e II é falsa

Ambas são verdadeiras

Sejam e bases de tais que

E seja a matriz tal que , para todo . Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Sejam Seja uma matriz tal que e . Se , então é igual a:

A matriz é tal que , e . A entrada da matriz é

(A)

(B)

(C)

(D)

Considere e a base Assinale a primeira entrada de, as coordenadas de na base .

(A)

(B)

(C)

(D)

A é uma matriz , da qual conhecemos apenas uma forma escalonada, a matriz, dada abaixo:

Podemos afirmar que a dimensão do espaço gerado pelas colunas de é:

(A)

(B)

(C)

(D)

Se , conjunto pode ser descrito como:

(A)

(B)

(C)

(D)

Sejam uma transformação linear e tais que .

Defina Considere as afirmativas abaixo:

I - Se é linearmente independente, então é linearmente independente.

II - Se é linearmente independente, então é sobrejetiva.

(A) Todas são verdadeiras.

(B) Todas são falsas.

(C) Apenas I é verdadeira.

(D) Apenas II é verdadeira.

Considere a matriz

a entrada da matriz é:

(A)

(B)

(C)

(D)

Seja uma matriz . Considere as afirmativas abaixo:

I - Se então admite infinitas soluções.

II - Se então tem solução única

para todo