Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 5
Sendo um tetraedro regular de aresta unitária, calcule .
Passo 1
No tetraedro regular, os pontos , e estão na mesma face, que é um triângulo equilátero de lado :
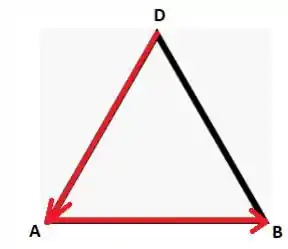
O ângulo entre os vetores e é .
Passo 2
O produto escalar é dado por
Mas como os lados são unitários, . Assim,
Resposta
Exercícios de Livros Relacionados
Seja W um subespaço de R n . Mostre que o conjunto de todos os vetores ortogonais a todos os vetores de W é um subespaço de R n . Este subespaço é chamado de complemento ortogonal de W e denotado por
Use o processo de ortogonalização de Gram-Schmidt para encontrar uma base ortonormal de R 3 que tem como base { ( 1,1 , 1 ) , ( 0,1 , 1 ) , ( 1,2 , 3 ) } .
Considere as retas ( x , y , z ) = t ( 1,2 , - 3 ) e ( x , y , z ) = ( 0,1 , 2 ) + s ( 2,4 , - 6 ) em R 3 . Encontre a equação geral do plano que contém estas duas retas e ache um subconjunto com o ma
Ache as equações dos planos em R 3 ortogonais ao vetor ( 2,2 , 2 ) , que distam 3 do ponto ( 1,1 , 1 ) . Estes planos são subespaços de R 3 ? Caso afirmativo, encontre base(s) ortonormal (is) para ele
Sejam U e V vetores no espaço, com V ≠ 0 - .a) Determine o número α , tal que U - α V seja ortogonal aV .