Responde AĂ­
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

CĂĄlculo NumĂ©rico - Franco e Neide B - CĂĄlculo NumĂ©rico- Ed: 1Âș - CapĂ­tulo 2.ExercĂ­cios complementares - Ex. 17

Seja o sistema đč 2,3 , − 1,2 . Exiba todos os nĂșmeros representĂĄveis neste sistema e coloque-os sobre um eixo ordenado.

Passo 1

Salve colega! Vamos representar todos os nĂșmeros possĂ­veis nesse sistema binĂĄrio. VocĂȘ jĂĄ deve estar craque nos conceitos da aritmĂ©tica de ponto flutuante, mas sĂł para manter o costume vamos lembrar da forma padrĂŁo de representação dos computadores que Ă© dada por:

đč đ›œ , 𝑡 , 𝑚 , 𝑀

Em que đ›œ   Ă© a base, 𝑡   Ă© o nĂșmero de dĂ­gitos na mantissa, e 𝑚 ,   𝑀 formam o intervalo de expoentes.

±   0 . 𝑑 1 𝑑 2 𝑑 3   ×   đ›œ 𝑒

PossĂ­veis mantissas :

±   0.100    

±   0.101    

±   0.111    

PossĂ­veis bases:

đ›œ =   2 − 1 ,   2 0 ,   2 1 ,   2 2

Passo 2

Agora temos que multiplicar cada mantissa por cada possĂ­vel base:

±   0.100   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.25 ,   0.5 ,   1.0 ,   2 10

±   0.101   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.3125 ,   0.625 ,   1.25 ,   2.5 10

±   0.111   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.4375 ,   0.875 ,   1.75 ,   3.5 10

Passo 3

Todos os nĂșmeros foram representados, agora Ă© sĂł colocar em um grĂĄfico, cada nĂșmero no eixo x.

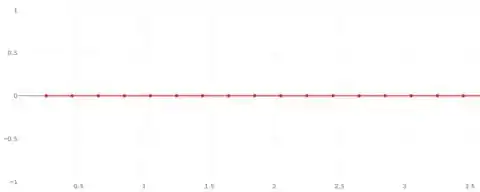
Finalizamos aqui!

Resposta

±   0.100   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.25 ,   0.5 ,   1.0 ,   2 10

±   0.101   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.3125 ,   0.625 ,   1.25 ,   2.5 10

±   0.111   ×   2 − 1 ,   2 0 ,   2 1 ,   2 2 = 0.4375 ,   0.875 ,   1.75 ,   3.5 10

ExercĂ­cios de Livros Relacionados

Escreva um programa em alguma linguagem para obter o resultado da seguinte operação: S = 10000 - ∑ k = 1 n x para: a) n=10000 e x= 0.1; b)n=80000 e x=0.125.
Considere uma mĂĄquina cujo sistema de representação de nĂșmeros Ă© definido por: ÎČ = 10 ,t = 4 , l = - 5eu = 5 . Pede-se:qual o menor e o maior nĂșmero em mĂłdulo representados nesta mĂĄquina? como serĂĄ re
Seja um sistema em aritmĂ©tica de ponto flutuante de quatro dĂ­gitos, base decimal e com acumulador de precisĂŁo dupla. Dados os nĂșmeros: x = 0.7237 × 1 0 4 , y = 0.2145 × 1 0 - 3 e z = 0.2585 × 1 0 1 Ef
Deseja-se calcular e - 0,15 . a) obtenha através de uma calculadora o valor exato de e - 0,15 . b) considere o sistema F ( 10 ,5 ,10 ,10 ) e a série truncada em 25 termos. Calcule:b1) e - 0,15 b2) 1 e
Se a , bec são reais e a ≠ 0 então a equação a x 2 + b x + c = 0 É satisfeita para exatamente dos valores de x : ( I ) x 1 = - b + b 2 - 4 a c a x 2 = - b - b 2 - a c 2 a Entretanto, desde que, a x 2