Teorema do Valor Intermediário e Funções Monótonas
Teoria
Lembra do teorema do valor intermediário?
Ele diz que, se uma função é contínua, para ir de um ponto para outro , ela deve, necessariamente, passar por todos os pontos entre e .
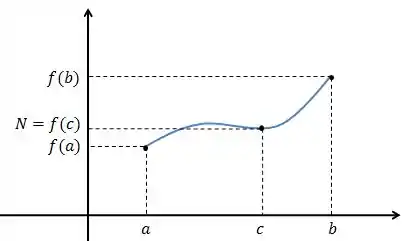
Isso significa que, se é negativo e é positivo ou vice-versa, temos uma raiz em , pois a função precisa passar por zero em algum momento.
Teorema do valor intermediário e funções monótonas
Ok, então usando TVI, conseguimos mostrar que existe uma raiz num intervalo que segue as condições do parágrafo anterior.
Mas e se quisermos mostrar que esta é a única raiz no intervalo?
Bem, para que seja a única raiz no intervalo, a função não pode voltar para zero. E como a gente pode garantir que a função não volta para zero? Ham, Ham, HAM?
Quando a primeira derivada não muda de sinal no intervalo, oras. Quando a derivada é sempre positiva, a função vai sempre crescer. Quando a derivada é negativa, a função vai sempre decrescer. Se ela passa por zero, não mais voltará!
Então, para garantir que uma função tem somente uma raiz num intervalo , precisamos aplicar o TVI e mostrar que a função é monótona no intervalo , ou seja, não muda o sinal da derivada nesse intervalo.
Teorema do valor intermediário e funções monótonas
Exercícios Resolvidos
Exercício Resolvido #1
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 285-17. MODIFICADO
Mostre que a função abaixo tem exatamente uma raiz no intervalo dado.
Passo 1
Na fronteira esquerda do intervalo:
Que é negativo.
A fronteira à direita é , então aplicamos limite para testar o sinal por lá:
Que é positivo.
Como temos um valor negativo na fronteira esquerda do intervalo e outro positivo na fronteira direita, então, pelo TVI, existe uma raiz para .
Passo 2
Agora, para esta ser a única raiz, precisamos mostra que a função é monótona. Para isso, derivamos:
Como a raiz quadrada é sempre um número positivo, temos a soma de números positivos. Portanto, é sempre maior que zero o que garante que a solução é única.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 285-22. MODIFICADO
Mostre que a função abaixo tem exatamente uma raiz no intervalo dado.
Passo 1
Na fronteira esquerda do intervalo, a função não está definida, devido a cotangente que não existe em 0. Então, usamos o limite:
Que é negativo.
Na fronteira direita do intervalo, a função também não está definida, devido a tangente. Então, usamos novamente o limite:
Que é positivo.
Como temos um valor negativo na fronteira esquerda do intervalo e outro positivo na fronteira direita, então, pelo TVI, existe uma raiz para
Passo 2
Agora, para esta ser a única raiz, precisamos mostra que a função é monótona. Para isso, derivamos:
Precisamos mostrar que a derivada é sempre positiva ou negativa. Lembrando que:
E:
Assim:
Os termos quadráticos serão sempre positivos. Acrescidos de , a derivada será sempre maior que zero. Há, portanto, somente uma raiz na história.
Resposta
Ei, a resposta está no passo a passo :)