Taxa de Crescimento e Decrescimento
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí! Vamos aprender um pouco sobre taxa de crescimento e decrescimento e aplicações da mesma?
PARTIU !
Dá uma olhada no gráfico dessa função aqui:
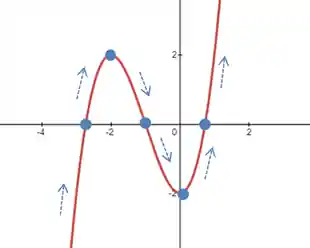
Olhando o gráfico a gente consegue ver que tem intervalos em que a função tem uma taxa de crescimento e outros em que a função tem uma taxa de decrescimento, não é?
Conseguimos dizer claramente que:
- A função deccresce no intervalo
- setinhas estão para baixo, e; - A função cresce no intervalo
- setinhas estão para cima.
Mas... e se ao invés de fornecer o gráfico a questão fornecer a expressão da função. Como achamos o intervalo nos quais ela crece e decresce?

É aí que entra o nosso conteúdo de hoje 🙂
Teste de Crescimento e Decrescimento
Esse teste nada mais é que uma forma rápida da gente achar os intervalos onde uma função é crescente e onde ela é decrescente e é MUITOOO útil para esboço de gráficos.
Esse teste dis o seguinte:

Agora vamos ver como aplicamos esse teste na prática. Considere essa função aqui:
A primeira coisa que vamos fazer é encontrar a deivada dessa função:
Agora, o que temos que fazer é estudar o sinal dessa derivada para saber quando ela será positiva e quando será negativa.
Para fazer isso, vamos separar a função em dois termos:
Agora, vamos construir o que chamamos de quadro de sinais: Na primeira linha coloque em ordem crescente as raízes de todos os termos e na primeira coluna coloque os próprios termos, a derivada e a função original, assim:

Agora vamos preencher as duas primeiras linhas do quadro analisando o sinal dos termos em cada intervalo. Desse jeito aqui:

Agora, a linha da derivada vamos preencher fazendo a multiplicação dos sinais de cada termo (isso porque a derivada é uma multiplicação dos termos, se fosse uma divisão você teria que dividir os sinais, beleza?)

Por fim, aplicamos o teste de crescimento e decrescimento, onde a derivada é positiva a função cresce e onde é nagativa a função decresce:

Sacou a dinâmica? Bora fazer mais exercícios para fixar bem?