Concavidade
Teoria
Faaala gente, você já deve ter se deparado em algum momento com a ideia de concavidade de uma função. Lá no ensino médio, aprendemos uma regrinha para saber quando temos a concavidade para cima (ou para baixo) em uma função do segundo grau.
Mas e se temos uma função, tipo essa aqui?
Como sabemos que concavidade ela vai ter?
Para nos ajudar com esse problema, vamos ter a ajuda da nossa querida derivada.
Então hehe, chegou a hora de a gente estudar a concavidade de umas funções!
Ok, ok. Talvez concavidade não seja um assunto tããão empolgante assim, mas você vai ver que isso tudo é bastante útil, prometo.
Antes de falar quando uma função é côncava para cima ou para baixo, vamos relembrar o que é concavidade em si. A concavidade é a “concha” da função.
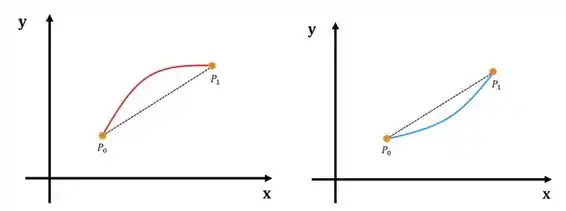
Chamamos a função à esquerda (em vermelho) de côncava para baixo e a da direita (em azul) de côncava para cima.
Então, com essa ideia vamos ver algumas funções.
Concavidades em funções do segundo grau
Mas antes de partimos para o universo das derivadas, nós todos estudávamos concavidade em funções do segundo grau no colégio. Vamos recordar a regrinha da concavidade?
Nós tínhamos um polinômio de segundo grau da forma:
E a concavidade era pra cima quando:
E para baixo quando:
Uma forma de você lembrar isso tudo é se preocupando com os sentimentos da função e notando que ela pode estar triste ou feliz, conforme você pode observar abaixo. Quando o é positivo, é sexta-feira, a função sorri e é côncava para cima:
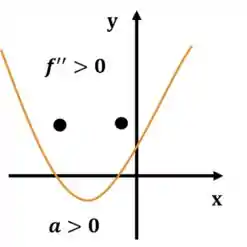
Quando é negativo, é segunda-feira e ela está triste. Esses olhos no gráfico da função estão aí para interpretação das atrizes-parábolas serem mais convincente:
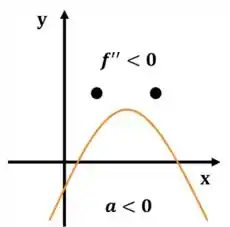
Concavidade por meio da derivada segunda
Em casos maais difíceis, como a que vimos no início:
Não temos como descobrir só batendo o olho nela, se a concavidade é para cima ou para baixo.
Para isso, vou te falar de um truque que a derivada faz pra gente, é só seguir esses dois passos aqui:
1º Passo: Pega a função e deriva ela duas vezes, ou seja, pega a derivada segunda.
2º Passo: Estuda o sinal de , onde ela for positiva a concavidade vai ser para cima. E onde ela for negativa a concavidade é para baixo.
Então, vamos fazer o nosso exemplo:
1º Passo: Pega a função e deriva ela duas vezes, ou seja, pega a derivada segunda.
Derivando a primeira vez:
Derivando novamente:
2º Passo: Estuda o sinal de , onde ela for positiva a concavidade vai ser para cima. E onde ela for negativa a concavidade é para baixo.
Ou seja, queremos saber quando e
Então:
Como é uma exponencial, ela nunca vai ser menor que 0, podemos elevar a qualquer número e sempre vai ser positivo.
Assim, precisamos estudar o sinal apenas de , quando ela for positiva, vamos ter positivo com positivo se multiplicando e o resultado vai ser positivo. E quando for negativo teremos positivo com negativo que resulta em negativo.
Assim:
E vai ser negativa quando:
Assim, antes do a função tem concavidade pra baixo e quando x for maior que a função tem concavidade para cima.
Agora, vamos experimentar aplicar a regra da derivada segunda para observar a regrinha da função do segundo grau?
1º Passo: Pega a função e deriva ela duas vezes, ou seja, pega a derivada segunda.
2º Passo: Estuda o sinal de .
A regra nos diz que a concavidade é para cima quando e para baixo quando .
Não é a mesma coisa? Sim, essa constante “” que apareceu não influencia em nada na inequação! As regras são equivalentes, só que a nossa regra de derivada segunda é mais genérica, isto é, ela vale para todas as funções.
Pontos de inflexão
Já vimos que a concavidade é para cima quando e para baixo quando . Mas e quando ?
Esse é o nosso querido ponto de inflexão.
Esse ponto é elemento importante e que ajuda bastante na hora de construir os e ele nada mais é do que o ponto onde a função troca a concavidade.
Se estava pra cima, passa a ser pra baixo, e vice-versa. Mas você pode estar se perguntando: “E como eu acho esse ponto?” Muito simples. Basta achar as raízes da derivada segunda! Vamos ver com mais detalhe no exemplo.
Um exemplo bacana de concavidade é a função . Dá pra enxergar direitinho que a concavidade dela muda na origem:
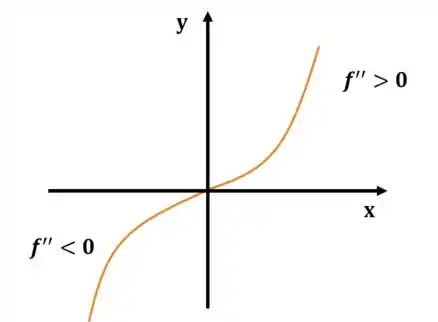
Pois temos que e, portanto, . Agora, qual o valor de pra que ? Ou seja, qual a raiz de ?
Nesse caso, a raiz da derivada segunda, , é . Assim, o ponto é um ponto de inflexão pra função . Então, como podemos ver no desenho, esse é o ponto onde a concavidade muda: antes era para baixo, depois foi para cima.
Concavidades em funções do segundo grau
Concavidade por meio da derivada segunda
Pontos de inflexão
Exercícios Resolvidos
Exercício Resolvido #1
UERJ - Cálculo 1 - Professora Renata - Lista Derivadas – 16 - Modificado
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Passo 1
Como estamos tratando de concavidade e ponto de inflexão, devemos calcular a derivada segunda. Calculando a primeira derivada antes (para chegar na segunda, precisamos passar pela primeira):
Olha lá, usando a regra do quociente, a segunda derivada:
Dividindo em cima e em baixo por , temos:
E por fim:
Passo 2
Legal, agora vamos analisar o sinal. Olhando para o denominador primeiro, o termo por si só não tem raiz e é sempre positivo. Quando elevado ao cubo ele se mantém sempre positivo. No fim, tudo se resume ao sinal do termo superior:
Para analisarmos o sinal do termo superior, vamos fazer as raízes de , vamos ter:
Com essas raízes, temos 3 intervalos pra checar:
Testamos o sinal escolhendo um valor dentro de cada um desses intervalos, como a segunda derivada só muda de sinal nas raízes, o sinal de qualquer valor escolhido dentro de cada intervalo será verdade para todo o intervalo. Agora, qual valor escolher? O que for mais conveniente.
Passo 3
Dá para gente escolher para o primeiro, para o segundo e para o terceiro. Vamos lá:
Ora, vemos que só é negativa dentro do intervalo . Isso significa que a função é côncava para cima para todo , menos quando , onde ela é côncava para baixo.
O ponto de inflexão é aquele onde a segunda derivada muda de sinal e, portanto, aquelas raízes que a gente achou:
Se você prefere pelo quadro de sinais:
Resposta
Pontos de inflexão:
Exercício Resolvido #2
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 302-78.
O que se pode dizer sobre o gráfico de uma função que possui uma segunda derivada contínua que nunca é zero? Justifique sua resposta.
Passo 1
Bem, a questão está perguntando sobre a influência da segunda derivada no gráfico, dadas as condições.
Vimos na teoria que a segunda derivada está relacionada com a concavidade do gráfico, então temos que concluir algo a respeito disso.
Passo 2
Pois bem, quais são as informações quanto à segunda derivada? Ela é contínua e nunca é zero.
Ok, para uma segunda derivada contínua (e qualquer função contínua no geral) mudar de sinal, ela precisa passar por zero (ser igual à zero) em algum momento.
Do contrário, ela saltaria de um valor negativo para um positivo ou vice-versa e isso não pode, pois a segunda derivada é continua e, sendo assim, não dá saltos.
Assim, como a segunda derivada nunca é zero, ela não muda nunca de sinal.
Finalmente, se a segunda derivada nunca muda de sinal, o gráfico terá sempre a mesma concavidade, para cima ou para baixo ;-).
Resposta
Ela não muda sua concavidade
Exercício Resolvido #3
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Passo 1
Como estamos tratando de concavidade e ponto de inflexão, devemos calcular a derivada segunda. Calculando a primeira derivada antes (para chegar na segunda, precisamos passar pela primeira):
E derivando mais uma vez, pescamos a seguinte função:
Passo 2
Legal, agora vamos analisar o sinal da segunda derivada. Pra gente ver o sinal, temos que igualar a , beleza? Então saca só:
Eita, e agora? Bem, se lembrarmos da definição das funções hiperbólicas:
Ficamos com:
Então ficamos com um ponto de inflexão só!
Passo 3
Pra saber agora quando que a concavidade é pra cima a gente tem que achar quando a segunda derivada vai ser maior que zero:
Então a concavidade pra cima é:
(os intervalos são abertos, heim... porque 8 não entra por ser o ponto de inflexão)
Passo 4
Pra saber agora quando que a concavidade é pra baixo a gente tem que achar quando a segunda derivada vai ser menor que zero:
Então a concavidade pra baixo é:
Resposta
Ponto de inflexão:
Concavidade pra cima:
Concavidade pra baixo:
Exercício Resolvido #4
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Passo 1
Como estamos tratando de concavidade e ponto de inflexão, devemos calcular a derivada segunda. Um truque aqui pra calcular a derivada vai ser lembrar que:
Como trabalhar com módulo de é complicado, vamos usar a definição pra reescrever:
Como é sempre positivo:
Nós fizemos isso porque a derivada de é mais tranquila de fazer do que de , saca só:
Podemos reescrever então a função para:
Calculando a primeira derivada antes (para chegar na segunda, precisamos passar pela primeira):
Fazendo a segunda derivada:
Passo 2
Legal, agora vamos analisar o sinal. Olhando para o denominador da primeira parcela, vemos que o ponto é um ponto que da problema por gerar uma indeterminação. Então salva ai esse ponto. Agora, vamos analisar o sinal da segunda derivada. Pra isso, só partir pro clássico “deriva e iguala à ”. Simbora:
Opa, dois pontos de inflexão e um ponto que a segunda derivada não esta definida. Show, vamos analisar então o sinal dela para os intervalos
Passo 3
Como os intervalos são
Vamos escolher valores que estejam dentro desse intervalo, beleza? Pro primeiro, se eu escolher
Pro segundo intervalo, vamos usar :
Pro terceiro intervalo, vamos usar :
E pro último intervalo, vamos usar pra testar, ficamos com:
Como a concavidade é pra cima quando e pra baixo quando , fechamos a questão! A resposta final vai ser:
Resposta
Pontos de inflexão:
Exercício Resolvido #5
Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Encontre os pontos de inflexão da função.
Passo 1
Como estamos tratando de concavidade e ponto de inflexão, devemos calcular a derivada segunda. Calculando a primeira derivada antes (para chegar na segunda, precisamos passar pela primeira):
E a segunda derivada:
Passo 2
Legal, agora vamos analisar o sinal. Olhando para o denominador do segundo termo, vemos que é um ponto que dá problema. Até porque é uma indeterminação!
Show, então vamos guardar esse ponto no bolso e vamos partir pros pontos que zeram a segunda derivada, beleza? Simbora:
E temos só um ponto de inflexão!
Passo 3
Agora que a gente sabe o ponto de inflexão vamos testar alguns valores pra vermos o sinal da derivada, ok? Os valores, já que temos e como pontos interessantes, vão ser valores nesses intervalos:
Pro primeiro intervalo, vamos testar
Pro segundo intervalo, vamos testar
E pro último, vamos testar :
Como a concavidade é pra cima quando e pra baixo quando , vamos ficar com:
Resposta
Pontos de inflexão: