Derivadas de Funções Básicas
Teoria
Fala Aí! Belezinha?
Vamos continuar nossos estudos sobre derivadas e agora veremos como derivar algumas funções básica que sempre acompanharão a gente nas matérias de cálculo.
Derivada de Funções Trigonométricas:
Quando começamos a estudar as derivadas nós aprendemos a derivar, inicialmente, dois tipos de funções: as funções constantes e as funções polinomiais. Mas você saberia dizer qual a derivada dessa função aqui:
Eita, agora complicou, né? Essa função não é constante e nem um polinômio. Mas relaxa que temos um jeitinho todo especial pra derivar ela.
E aqui já vai um recado pra acalmar seu coração: Vamos falar agora das funções trigonométricas, mas em cálculo será bem mais tranquilo de trabalhar com elas do que pode ter sido no seu Ensino Médio. Isso porque as derivadas dessas funções já são tabeladas. Então, o que teremos que fazer é conhecer bem essa tabela. E é isso que faremos agora, vamos lá!
Mas quem são essas tais funções trigonométricas?
São essas aqui, ó:
- Seno ;
- Cosseno ;
- Tangente ;
- Secante ;
- Cossecante ;
- Cotangente .
Agora vamos aprender a derivá-las, começando pelas funções seno e cosseno, elas vão formar o nosso par principal e suas derivadas serão:
- A derivada do seno é o cosseno:
- A derivada do cosseno é o menos seno:
- A derivada da tangente que é secante ao quadrado:
- A derivada da secante que é tangente vezes secante;
- A derivada da cotangente que é menos cossecante ao quadrado:
- A derivada da cossecante que é menos cossecante vezes cotangente:
- A derivada de é o próprio . Assim:
- A derivada de é :
- A derivada de é sobre :
- A derivada de é sobre vezes :
Sei que é um pouco ruim ter que gravar as coisas, mas a demonstração dessas derivadas dá um trabalhão enorme e não é cobrada nas matérias iniciais de cálculo, então o jeito é a gente gravar mesmo. Mas depois de fazer bastante exercícios, você vai lembrar delas até mesmo dormindo rsrs.
Agora vamos ver as derivadas das outras funções trigonométricas que estão ali em cima. São elas:
Calma, calma, calma. Não briga comigo ainda. Sei que são muitas coisas pra lembrar e por isso vou te mostrar um jeito mais tranquilo de fazermos isso.
Vamos construir uma tabelinha onde a primeira linha será feita com as funções tangente, secante e secante. Fácil de lembrar isso, né? Tangente, secante e secante! Vamos lá, vai ficar assim:
Agora a segunda linha vai ser bem parecida, só que colocaremos o “co” na frente das funções, então será: cotangente, cossecante e cossecante. Último detalhe é que a cossecante do meio ganhará um sinal negativo. E vai ficar assim nossa tabela:
Agora, quando você quiser saber a derivada de uma dessas função trigonométrica você vai procurar ela nessa tabela. Sua derivada será o produto das funções que estiverem na mesma linha que ela. Veja os exemplos:
Qual a derivada da tangente?

E se eu te pedir a derivada da secante?

A mesma coisa vale para cotangente e cossecante, basta multiplicar as funções que estiverem na mesma linha: (fica ligado no sinal de menos que tem na cossecante do meio da tabela).
Para a derivada da cotangente:

E para a derivada da cossecante:
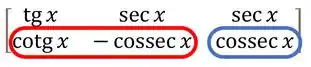
Fica bem mais tranquilo usando a tabelinha, né. Então agora é só praticar bastante!
OBS: Sobre as funções trigonométricas existem algumas relações que os exercícios podem cobrar, então é sempre bom a gente saber. São essas aqui:
E também é bom lembrar da relação fundamental:
Já temos bastante informação sobre as funções trigonométricas, agora vamos ver outro dois tipos de funções, as exponenciais e as logarítmicas. Vamos nessa!
Derivada de Exponencial
Nós já aprendemos a derivar funções polinomiais do tipo . Mas, e funções desses tipo aqui:
Opa, essa é diferente! Agora o está no expoente, e quando isso acontece temos uma função exponencial. Poderíamos ter qualquer valor na base, no exemplo é o , mas poderia ser o 2, o , ou qualquer outro valor constante.
E existe um valor constante que é especial, ele costuma aparecer bastante pra gente em cálculo. Esse valor é o número de Euler . Vamos começar a derivar as funções exponenciais que tem este número em sua base.
E essa é a derivada MAIS SIMPLES que existe, porque:
Tranquila essa, né?
Mas e se a base não for esse ? Vamos pensar em um número qualquer que vamos generalizar pra .
Como calcular a derivada dele agora? Bom, pra derivar esse carinha aí você repete o e multiplica por . Assim:
Esse é chamado de logaritmo neperiano de , que é o logaritmo de na base . Esse valor é um número constante que você pode até achar com uma calculadora, mas no geral daremos nossa resposta dessa forma mesmo. Sem procurar o valor de , só acrescentamos ele no final que já está lindo.
Recapitulando:
Então, se a base não for o , você acrescenta o da base no final.
Derivada de Função Logarítmica
Agora podemos atacar a função logarítmica. E aqui também existem dois tipos de funções logarítmicas que podemos encontrar, o que é o logaritmo na base , como vimos ali em cima, e o que é o logaritmo em qualquer outra base.
Vamos começar pelo mais simples que é o
Mas e se a base não for o pra ser o ? teremos um , e agora?
Bom, para derivar o , basta fazermos o e multiplicar o pelo , parecido como que fizemos para a derivada de . Vai ficar assim, ó:
Recapitulando:
Agora já sabemos muitas derivadas novas, e como vimos bastante coisa, aqui vai um resuminho esperto com as nossas novas derivadas:

Derivada de Exponencial
Derivada de Função Logarítmica
Exercícios Resolvidos
Exercício Resolvido #1
Derive a função
Passo 1
Bom galera, precisamos derivar a função . Mas tenha atenção! Essa função é a multiplicação entre dois números constantes o e o . Como a função é a multiplicação dessas duas constantes, então ela é uma função constante!
Vocês se lembram como se deriva uma função constante?
Derivar é a mesma coisa que calcular a taxa de variação! Se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Como não varia, sua derivada vale .
Ou seja a derivada de vale:
Já estamos craques em derivada de constante, né?
Resposta
Exercício Resolvido #2
Derive a função
Passo 1
Fala, galera! Com é que vocês estão? Muita ralação? Então agora pode relaxar, porque aqui vai ser tudo explicado passo a passo com muita calma!
Essa função pode te assustar um pouco por causa da variável . Estamos muito acostumados a fazer exercícios com . Mas se a gente substituísse esse por , o susto passaria?
Quando a gente substituiu por , a gente apenas mudou o nome da variável. Isso não muda em nada o passo a passo que vamos seguir para derivar a função! Isso quer dizer que o nome da variável não importa! Podemos derivar a função com , imaginando que estamos derivando uma função com , beleza? Então, vamos voltar para a função do enunciado!
Essa questão parece ser difícil, porque a função está escrita de uma maneira complicada. No entanto, nós podemos reescrever essa função de uma forma mais simples. Tá vendo esse na frente do parêntese? Ele está aí multiplicando todo mundo que está dentro dos parênteses. Vamos aplicar a multiplicação distributiva, “distribuindo” mesmo ele em todos os termos que estão lá dentro dos parênteses.
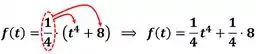
Agora temos uma multiplicação da fração por valores inteiros: e . Quando isso acontece a gente multiplica só a parte de cima e repete a pare de baixo:
A fração
Logo:
Essa nova função assusta menos, não é mesmo?
Agora que simplificamos a função, podemos começar a derivar.
Passo 2
Para derivar uma função com somas a gente lembrar que termos somados ou subtraídos podem ser olhados separadamente, assim a nossa vida vai ficar muito mais fácil! Levando isso em conta, a derivada de pode ser reescrita como está abaixo.
Sempre que a gente precisar derivar uma função grande cheia de somas e subtrações, podemos derivar cada termo de forma separada e depois juntar tudo para calcular a derivada da função inteira! Vamos calcular a derivada de cada termo separadamente no próximo passo!
Passo 3
Para calcular a derivada de , usaremos a regra do peteleco! Nessa regra, a derivada faz o expoente “cair” e passar a multiplicar o termo. Além disso, o expoente da derivada vira o expoente antigo menos .
No termo , o expoente vai “cair” e passar a multiplicar. O novo expoente será .
Como estamos multiplicando e dividindo por 4, as operações se cancelam e podemos cortar o em cima e embaixo.
Agora, vamos calcular a derivada da constante . Para isso, temos que lembra que derivar é a mesma coisa que calcular a taxa de variação! Se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Ou seja, como não varia em relação a , sua derivada vale .
Já que temos os valores de cada derivada, podemos juntar todos eles para calcular a derivada total da função .
Passo 4
Agora podemos substituir todos esses valores de derivadas na equação da derivada da função (segunda equação do passo 2).
Boaaa! Esse é o fim de mais um exercício de derivadas! Estamos voando!
Resposta
Exercício Resolvido #3
Encontre a derivada de segunda ordem da função
Passo 1
E aí, galera, como estão?
O exerício pede para a gente calcular a derivada de segunda ordem da função , mas o que isso significa? Significa que temos que derivar a função duas vezes! Ou seja, vamos derivar a função e depois derivar o resultado dessa primeira derivação!
Essa segunda derivada pode ser representada por:
O número indica que essa é a derivada.
Vamos começar então derivando a primeira vez. Essa função é composta por dois termos, mas não se assuste! Ao invés de derivar tudo de uma vez podemos derivar cada termo separadamente. Depois podemos juntar essas derivadas individuais e calcular a derivada total da função.
Então vamos calcular essas derivadas de forma separada no próximo passo!
Passo 2
Podemos derivar usando a regra do peteleco. Essa regra é usada, quando a variável (no caso a variável é o ) está elevada a um número constante que podemos chamar de . Quando derivamos um termo , o expoente do termo “cai” e passa a multiplicar. Além disso, passa a ter um novo expoente !
Mas cadê o tal do ? Então, quando o está sozinho desse jeito, parecendo que não há expoente , é porque o expoente é igual a .
Então:
Perfeito, agora da pra usar a regra do peteleco de boas!

Todo número elevado a zero é igual a , então
E finalmente:
Agora é a vez do . Ele é uma constante. Como a derivada é uma taxa de variação e constantes não variam, a derivada de vale zero!
Juntando a derivada dos dois termos, a primeira derivada vale:
Vamos deixar para o próximo passo o cálculo da segunda derivada!
Passo 3
Foi falado que, para encontrar a segunda derivada, precisamos derivar a função mais uma vez. Isso quer dizer que precisamos derivar o .
Como é uma constante, essa derivada é igual a zero!
Pronto! Chegamos ao fim de mais uma questão! Palmas pra gente!
Resposta
Exercício Resolvido #4
O valor de da função e de:
(a) .
(b) .
(c) .
(d) .
(e) .
Passo 1
E aí, tudo beleza?
Olha só, a gente quer o valor da segunda derivada de , que é, na verdade a derivada da derivada. Pra isso, primeiro a gente tem que calcular a primeira derivada, ok?
Vamos lá...
Passo 2
A função é é uma daquelas funções que a gente precisa ter sempre em mente. Então vamos lembrar que a derivada dela então é:
Tranquilo até aqui né?
Essa é a primeira derivada de !
Passo 3
Como a gente quer a segunda derivada, então precisamos lembrar que a derivada do será:
Show! Segunda derivada encontrada! 😉
Passo 4
A questão pede . Repara que o está justamente no lugar do em . Então a gente vai na nossa e substitui o por 0, beleza?
Prontinho! A alternativa correta é a letra ! 😊
Resposta
c) .
Exercício Resolvido #5
Encontre a primeira e segunda derivada da função .
Passo 1
Olá! Tudo joinha?
Vamos derivar essa função , beleza? A gente tem ali um polinômio que é uma função com varias potências de . Nesses casos a gente usa a “Regra do Tombo” ou do “peteleco”. Em cada termo daquele, o expoente vai cair pra frente do multiplicando, e ao cair ele perde uma unidade. Desse jeito aqui:
Tranquilo? Mãos à obra então!
Passo 2
Bom, outra coisa que é importante aqui é que quando tempos vários termos somados ou subtraídos em uma função, podemos fazer a derivada de cada um separadamente. A derivada da soma é a soma das derivadas. Então a gente pode derivar cada termo ali usando a Regra do Tombo mantendo a ordem das operações!
Vai ficar assim:
Lembrando que as constantes continuam ali pra multiplicar nosso expoente que acabou de “cair”.
Já montamos a regra, agora é só resolver essas continhas que ficaram...
Passo 3
Resolvendo ali, ficamos com:
Aqui a gente também precisa lembrar que todo número elevado a é 1, então isso é o mesmo que:
Prontinho! Essa é a primeira derivada 😄
Passo 4
Agora a gente vai ver a segunda derivada! Vamos fazer da mesma forma, só que agora derivando !
Detalhe importante: a derivada de uma constante é sempre zero! Como:
Podemos fazer a derivada de cada termo separado novamente:
Resolvendo, temos:
E essa é a segunda derivada! Acabamos uhull!!
Resposta
Exercício Resolvido #6
Encontre a primeira e segunda derivada da função
Passo 1
Fala aí! Tudo joia?
Essas raízes ai podem até confundir um pouco a nossa mente no começo, mas pra gente derivar essa função, vamos usar a “Regra do Tombo”. Em cada termo daquele, o expoente vai “cair” pra frente multiplicando e vai perder uma unidade. Desse jeito aqui:
E você dever estar se perguntando: mas que expoente, gente? Bem, quando temos uma raíz, podemos reescrevê-la em forma de potência, e esse será o nosso primeiro passo.
Passo 2
Para reescrever as raízes em forma de potências, precisamos usar essa regra aqui:
Nossa raíz será transformada em uma potência onde o expoente é uma fração. No numerado (parte de cima da fração) vai ficar o valor que o estiver elevado antes quando ainda estava dentro da raíz, e no numerador (parte de baixo da fração) vai ficar o índice da raíz.
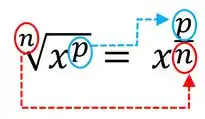
Então no nosso caso, em não aparece valor nenhum, isso porque é uma raíz quadrada, então o índice da raíz e o . Além disso, o não está elevado a número nenhum, e pra ajudar a gente, vamos colocar o 1 no expoente dele. Vai ficar assim:
E para o
Nossa função então pode ser escrita como:
Passo 3
Agora vamos partir pra usar a Regra do Tombo! Montando vai ficar assim:
Vamos dar um pause aqui na derivada e vamos resolver essa subtração entre frações, que está nos exponentes, no próximo passo...
Passo 4
A gente tem que resolver:
A gente só pode somar ou subtrair frações se elas tiverem os denominadores iguais, lembra?
Nesse caso aqui a gente pode fazer um esqueminha bem legal que é reescrever o como uma fração com o denominador que a gente precisa. Pra isso a gente vai dizer que nosso pode ser escrito com:
Agora que ele tem o denominador . Nossa continha fica:
Agora que os denominadores ficaram iguais, a gente resolve em cima, e embaixo a gente repete:
Na outra é a mesma coisa:
Agora já conhecemos os valores dos expoentes da nossa derivada.
Passo 5
Vamos voltar isso pra derivada agora:
Outro detalhe importante. Como os expoentes estão negativos, a gente vai jogar as potências pro denominador:
E agora a gente pode voltar pra forma de raiz:
Prontinho! Essa é a primeira derivada😉
Passo 6
Vamos pra segunda derivada agora. É da mesma forma, só que a gente vai derivar a função , beleza?
Pra facilitar um pouquinho, vamos pegar nessa forma aqui:
Show! Agora vamos aplicar a Regra do Tombo nela:
Passo 7
Essas continhas aí a gente vai resolver da mesma maneria que fizemos ali atrás! Vai ficar assim:
Vamos jogar o que tá com expoente negativo pra baixo:
E vamos colocar na forma de raiz:
E pronto! Essa é a segunda derivada 🤓
Resposta
Exercício Resolvido #7
Determine as derivadas de todas as ordens possíveis da função polinomial:
Passo 1
Opa! Tudo joia?
Pra começar, precisamos entender o que o enunciado quis nos dizer! O que nos foi passado é que vamos derivar essa função até encontrarmos zero no final. Assim teremos determinado TODAS as derivadas.
Relembrando, para fazermos a derivada de uma função polinomial, basta a gente colocar o nosso expoente para baixo multiplicando (na base) e subtrairmos 1 lá de cima no expoente (Regra do Tombo). Assim:
Beleza? Vamos lá!
Passo 2
Vamos fazer a nossa primeira derivada, ok? A gente vai derivar cada termo usando aquela Regra do Tombo que falamos ali no passo 1. Ah, lembra que derivada de constante é zero!
Agora a gente faz as multiplicações e resolve os expoentes:
Prontinho! Essa é a primeira derivada!
Passo 3
Vamos para a segunda derivada agora, a gente vai derivar o que a gente encontrou no passo anterior. Do mesmo jeitinho, olha só:
Resolvendo as continhas...
Show! Essa é a segunda derivada... respira, e vamos continuar!
Passo 4
Terceira derivada e lá vamos nós, mesmo esquema! Agora a gente deriva a que achamos ali em cima:
Prontinho! Mais uma/menos uma! 😊
Passo 5
Quarta derivada, let’s go! Derivamos a que encontramos ali em cima. Aí pra gente não ficar usando um monte de aspas, vamos escrever assim pra dizer que é a quarta derivada:
Vamos que ainda tem derivada!
Passo 6
Quinta derivada, agora...
(Estamos quase lá, se acalma haha...)
Opa! Chegamos numa constante hein...
Passo 7
Vamos ao nosso gran finale, sexta derivada! Já que a quinta deu uma constante...
E... ufaaa! Acabamos! Nossa função tem 6 derivadas então! Calculamos todas! Uhull!
😉
Resposta
Exercício Resolvido #8
Encontre uma equação para a reta tangente à curva no ponto dado.
Passo 1
Fala aí, tudo joia?
Olha só, sempre que falar de equação de reta tangente, a gente vai usar derivada!
Isso porque uma reta tem essa forma aqui:
Onde é a inclinação (coeficiente angular) da reta e é um ponto da reta.
E esse é justamente a o valor da derivada da função no ponto . Sacou?
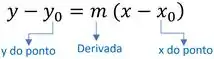
Bora ver isso na prática!
Passo 2
Como a gente precisa da derivada, vamos começar derivando a função:
A gente deriva com a regra do Tombo, que é assim:
Vamos derrubar esses expoentes então!
Beleza! Já derivamos a função!
Passo 3
Agora a gente precisa do valor dessa derivada no ponto que nos deram, no caso:
O ponto tem sempre uma ordem específica, primeiro o valor do e depois do valor do .
Então o ponto tem e .
Substituindo na nossa derivada o , a gente tem:
Esse aí é o coeficiente angular da reta, o nosso !
Passo 4
Voltando pra equação da reta tangente agora:
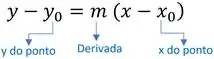
A gente já tem e temos o ponto . Só jogar ali agora e correr pro abraço!
O que podemos também fazer aqui é dar uma pequena arrumada. Vamos multiplicar esse 3 através da distributiva:
Agora vamos deixar o sozinho jogando o para o outro lado somando:
Prontinho! Essa é a equação da reta tangente no ponto pedido😉
Resposta
.
Exercício Resolvido #9
Encontre uma equação para a reta tangente à curva no ponto dado.
Passo 1
Olá! Olha só:
Devemos achar a equação da reta tangente a uma curva. Para termos a equação de uma reta, precisamos de um ponto e de sua inclinação.
O ponto já foi dado no enunciado. Já inclinação pode ser obtida derivando a função: ela é exatamente a derivada calculada no ponto.
A equação da reta com inclinação e que passa pelo ponto é:
![]()
Passo 2
Vamos começar derivando a função então!
Podemos reescrever a expressão da curva usando a regra de transformação da raiz em potência:
Vamos achar a inclinação com a derivada da função, usando nossa conhecida regra do Tombo:
Pra fazer aquela subtração com fração ali, vamos escrever o
Resolvendo aquela continha do expoente. Onde vamos subtrair em cima e repetir embaixo:
Assim:
Ainda podemos jogar esse expoente negativo pra baixo e voltar para a forma de raiz quadrada:
Passo 3
Como a gente quer o valor dessa derivada no ponto pra achar a inclinação, vamos substituir na derivada que encontramos e resolver:
Show! Achamos então a inclinação da reta, que é 😊
Passo 4
Montando a equação da reta tangente agora:
Temos e . Substituindo:
Agora é só dar aquela arrumadinha básica na resposta, por professor ficar feliz. Vamos tirar o zero que não faz diferença e fazer a multiplicação distributiva do em todo mundo que está dentro dos parênteses.
Prontinho! Essa é a equação da reta tangente no ponto pedido! 😊
Resposta
Exercício Resolvido #10
Quais são os valores de para os quais o gráfico tem tangentes horizontais?
Passo 1
E aí, como estamos indo?
Pra começar essa vamos pegar uma informação super importante: Toda reta horizontal possui coeficiente angular nulo, ou seja, .
E você lembra o que é o coeficiente angular da reta tangente? A derivada da função.
Ouuu sejaaaa... o que a gente tá procurando na verdade são os pontos onde a derivada da nossa função é zero!
Então, bora derivar e igualar a zero pra achar esses valores de aí que ele tá querendo?
Passo 2
Vamos derivar essa função aqui:
A gente usa a regra do Tombo, tá lembrado? Assim ó:
Vamos aplicar isso em cada termo, então:
Beleza! Achamos a derivada!
Passo 3
Agora a gente precisa achar os pontos onde essa derivada é zero, ou seja:
E isso aí virou uma equação de segundo grau.
Vamos resolver essa equação pela famosa fórmula de Bháskara! Que é assim:
Onde são os coeficientes da nossa equação. No nosso caso: .
Vamos começar achando o pra depois jogar isso ali na formula do .
Passo 4
Primeiro aqui:
Substituindo na outra relação:
Quando chega nessa fórmula, temos que separar ela em duas partes. Uma usando o e outra usando o pra
Bora fazer a parte da soma:
Ahhh uma coisa importante, podemos escrever a como .
Simplificando o :
Agora a subtração:
Prontinho! Esses são os pontos onde as tangentes são horizontais😊
Resposta
ou