Regra do Produto e do Quociente
Teoria
Regra do Produto
Oie, olha nós aqui outra vez, juntos em uma caminhada pelo estudo das derivadas. Até agora você já aprendeu a derivar funções importantes como polinômios e até mesmo funções trigonométricas. Vamos relembrar algumas:
Você se lembra como derivar ? Usamos a regra do peteleco. Assim:
E você se lembra da derivada de ? Essa é uma daquelas já tabeladas:
Maravilha! Mas e se a gente encontrar as duas juntas em uma única função, o que faremos?

Calma, calma! Aqui não podemos derivar cada uma separadamente e depois multiplicar, como fazemos quando temos uma soma ou uma subtração. Nesse caso teremos que usar a regra do produto.
A regra é essa aqui:
Ficou esquisito assim né? Vamos ler a regra que talvez ajude. Temos duas funções sendo multiplicadas. Então a derivada do produto dessas funções será:
“A derivada da primeira vezes a segunda, mais a primeira vezes a derivada da segunda”
Vamos olhar pra ela com mais calma. Essa primeira parte quer dizer que estamos derivando um produto de duas funções, uma que vamos chamar de e outra que vamos chamar de .
Assim, em:
E do lado direito da fórmula temos duas parcelas, onde a primeira é , e a segunda é . Reparou que cada parcela tem a derivada de uma das funções vezes a outra? É como se a gente estivesse distribuindo as derivadas e cada função fosse ganhar a sua em uma parcela.
Veja que vamos precisar das funções e das suas derivadas pra montar a regra. Então, vamos fazer as derivadas de cada uma das funções e já deixar reservado:
Feito isso, a gente aplica tudo na fórmula:
Assim:
Então o lance é aplicar a fórmula!
Prontinho, agora está derivado. Essa regrinha é muito, muito importante, então é sempre bom praticar com bastante exercício!
Regra para produto de 3 funções
E se ao invés de duas, tivermos três funções sendo multiplicadas?
Lembra que nossa derivada fica distribuída e cada função ganha a sua em uma parcela? Então, aqui também será assim, e pra isso teremos parcelas, onde a primeira parcela terá a derivada da primeira função vezes as outras funções, a segunda terá a derivada da segunda função vezes as outras e a terceira terá a derivada da terceira função vezes as outras.
Assim, fazemos:
E a derivada vai ser:
Como vamos precisar das derivadas de cada uma, vamos já encontrá-las e deixar reservado aqui:
Agora a gente aplica a regra do produto da forma como acabamos de ver:
Ficando com:
Prontinho, derivada!
OBS: Se tivéssemos um produto com ainda mais funções, uma quantidade qualquer que vou chamar de , esse mesmo padrão seria gerado. Teríamos como resultado parcelas onde em cada uma, uma das funções está derivada:
Regra do Quociente
Beleza, já avançamos bastante! E se de repente aparece no meio dos nossos exercícios algo desse tipo aqui:
Como encontrar a sua derivada?

Pois é! Essa função aí não é um produto, então não rola de aplicar a regra do produto pra encontra a derivada dela. Ela é um quociente entre funções, que é na verdade a divisão dessas funções.
Mas para funções desse tipo, também temos uma regrinha toda especial. E o melhor, ela é parecida com a anterior! A diferença é que ao invés de somar, nós iremos subtrair as parcelas e no final a gente divide pela segunda função ao quadrado.
Vamos chamar de primeira função a que estiver no numerador e de segunda a que estiver embaixo, no denominador. Assim, a regra se lê:
“A derivada da primeira vezes a segunda, menos a primeira vezes a derivada da segunda, tudo dividido pela segunda ao quadrado”
Vamos ver como fica a derivada da nossa função
Fazendo
Como precisaremos de suas derivadas, vamos calcular antes e já deixar aqui reservado:
Show, agora vamos aplicar isso na regra do quociente:
Pra ficar bonito mesmo, a gente só arruma o denominador que está com uma potência de potência. Quando isso acontece a gente repete a base e multiplica os expoentes, ficando com:
E assim, aplicamos a nossa regra do quociente. E pra ficar fera mesmo, o lance é partir para os exercícios. Então a gente se encontra lá de novo!
Regra para produto de 3 funções
Regra do Quociente
Exercícios Resolvidos
Exercício Resolvido #1
A derivada da função é:
Passo 1
Beleza, pessoal! Essa é uma questão onde precisamos derivar a tangente ao quadrado. Você pode estranhar a primeira vista! Aprendemos a derivar , mas ainda não aprendemos a derivar . É aí que você se engana! Nós já conseguimos derivar essa função trigonométrica, se a gente lembrar que:usando:
Se a gente lembrar que que o expoente 2quando elevamos algo ao quadrado, significa que vamos multiplicar ele por ele mesmo significa que o termo aparece na multiplicação 2 vezes, a gente converte uma exponenciação em uma multiplicação!o que era um potência vira uma multiplicação.
E pra dDerivar uma multiplicação éa gente já sabe! É só seguir a regra do produto!
Usaremos a regra do produto no próximo passo.
Passo 2
Antes de lembrar da regra do produto, vamos dar nomes aos dois termos da multiplicação.
Ou seja, chamamos a primeira tangente de e a segunda tangente de .
Depois dar nomes a cada termo da multiplicaçãoFizemos isso porque agora, nós podemos escrever a regra do produto, que tem esse formatinho aqui: ela diz que a derivada de vale:
Traduzindo: A derivada da nossa função é igula a derivada de vezes mais vezes a derivada de .
Lembre-se que usamos o símbolo (também chamado de apóstrofo) para representar as derivadas! Logo:
Isso quer dizer Já sabemos que é e quem é , agora que precisamos calcular quanto vale as derivadas de e para resolver a questão! No passo seguinte vamos calcular isso!
Passo 3
Como , a A derivada de é a derivada da tangente! Para lembrar das derivadas das funções trigonométricas (seno, cosseno, tangente, etc.), podemos usar a imagem abaixo.

Pela imagem nós vemos que a derivada da tangente é secante ao quadrado:
E como , aA derivada de também é a derivada da tangente. Ou seja:
Nós já calculamos a derivada de cada termo da multiplicação. Na última etapa da questão, vamos aprender a substituir todas essas derivadas na fórmula de da derivada de .
Passo 4
Substiutindo , e na regra do produto, achamos:
A equação acima é a soma de dois termos iguais. Por causa disso:
Ou seja, a resposta certa é a opção (aa).
Resposta
Letra (aa)
Exercício Resolvido #2
Derive a função
Passo 1
Essa derivada pode parecer difícil porque tem essa letra nela. Mas o que ela significa? Ela é uma constante muito comum em problemas de cálculo e física. É um número que vale aproximadamente .
Mas não precisamos nos preocupar com ele não, pois sempre vamos usar a própria letrinha em nossas soluções.
Agora a função é composta por uma divisão. Nesse caso, como fazemos para derivar?
Pra ajudar a gente a derivar uma divisão, temos que dar nomes para cada termo que aparece ali. Com isso a derivada vai ficar mais organizada. Vamos chamar o termo de cima da fração de e o termo debaixo de .
Usando e podemos reescrever da seguinte forma:
Mas como dar nomes ao termo de uma divisão pode organizar a resolução da questão?
Veremos isso no próximo passo!
Passo 2
Para derivar uma divisão entre funções (divisão que tem embaixo e em cima), usamos uma regra chamada de regra do quociente.
No passo anterior, a gente deu nome a cada termo da divisão, isso porque a regra do quociente é feita usando esse formato aqui:
Lembre-se que usamos o símbolo (chamado de apóstrofo) para representar as derivadas! Ou seja, é a derivada de , é a derivada de e é a derivada de !
Isso significa que precisamos calcular as derivadas de e para achar .
No próximo passo, vamos calcular quanto e valem!
Passo 3
Nesse passo, temos que calcular quanto vale a derivada de e a derivada de .
Vamos começão por ! é a função exponencial que é a mais fácil de derivar! A derivada de é a própria exponencial .
Vamos deixar ela anotadinha aqui que já já a gente vai usar.
Essa foi tranquila, né? E a derivada de ? Você se lembra como derivar?
É através da regra do peteleco! Nessa regra, o expoente “cai” na frente do e deixa pra trás ele mesmo menos .
Aplicando essa regra em , temos que:
Pronto! Achamos quanto vale e quanto vale .
Agora só falta substituir esses dois termos na regra do quociente para calcular .
Passo 4
Substituindo , , e na regra do quociente.
E vai ficar assim:
Que equação enorme! Ainda por cima tem um embaixo dela! Vamos arrumar isso?
Sempre que tiver um número sendo elevado duas vezes, repetimos a base e multiplicamos seus expoentes!
Substituindo isso na equação de :
Essa equação ainda está enorme! Podemos simplificar . No próximo passo faremos isso!
Passo 5
Perceba que “” multiplica o termo “” e o termo “” da equação, então podemos dizer que ele é um fator comum. Por conta disso, podemos colocar “” e “” dentro de um parênteses e deixar “” fora para mostrar que multiplicam esses dois termos ao mesmo tempo. Chamamos isso de “colocar o em evidência”
Se olharmos com mais cuidado, vamos ver que isso também está acontecendo com o . Dentro dos parênteses temos o elevado a , que indica que o está sendo multiplicado 2 vezes.
Assim, a gente consegue reescrever a equação de .
Agora nós vemos que o termo “” está presente nos dois termos que estão dentro do parênteses. Logo, também podemos colocar o “” em evidência e mostrar que ele multiplica esses dois termos ao mesmo tempo.
Com isso fora do parênteses, ficamos com “” em cima e embaixo. Isso quer dizer que podemos simplificar o de cima com o que está em baixo .
Pra isso vamos pensar que , então vamos cortar um de cima com um de baixo.
Pronto! Aqui nós paramos, pois não podemos simplificar mais que isso. Assim nós derivamos e achamos uma versão mais simples de !
Resposta
Exercício Resolvido #3
Derive a função
Passo 1
E aí, tudo beleza?
A gente quer a derivada dessa função e repara que ela é formada por uma multiplicação do pelo . Ou seja, o produto de dois fatores, certo?
Pra derivar isso, a gente usa a Regra do Produto, que é assim:
Onde a “ ” significa derivada, ok?
Passo 2
Agora pra continuar, a gente tem que definir quem serão as nossas funções e . Se a gente olhar lá pra nossa função , a gente pode ver isso aqui:
Então: e .
Mas na regra do produto também precisamos de e de Vamos derivar essa agora, pra depois montar nossa Regra do Produto😚
Passo 3
é um polinômio, a gente já sabe derivar tranquilinho né?
E é mais fácil ainda, porque a derivada da exponencial é ela mesma😉
Prontinho! Já temos todos os nossos ingredientes para montar a Regra do Produto!
Passo 4
Montando...
Pra ficar mais bonitinho, a gente pode reagrupar isso, colocando o em evidência, já que ele está em todos os fatores:
E acabamos por aqui! Essa é a nossa derivada😉
Resposta
Exercício Resolvido #4
Derive a função
Passo 1
Olá! Bora resolver mais essa?
Queremos derivar essa função e ela é formada por uma multiplicação. Daí a gente já sabe que vamos ter que usar a regra do Produto, certo?
Só pra relembrar, a regra do Produto é assim:
Sendo que o “ “ representa a derivada da função😉
Passo 2
Vamos definir agora quem é e quem é . A ordem não importa, mas vamos chamar assim:
Então temos:
Show! Agora vamos derivar cada uma dessas, porque na regra do produto precisaremos de e ...
Passo 3
Derivando ...
Temos que é uma soma entre uma potência e uma exponencial. A gente pode derivar cada termo e manter a soma. Potência e exponencial a gente já aprendeu a derivar, lembra? Vai ficar assim:
Como qualquer coisa elevada a zero dá um:
Beleza, já derivamos !
Passo 4
Vamos derivar agora. Veja que, podemos escrever como usando essa regrinha aqui:
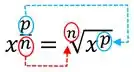
Com isso, podemos escrever assim:
Agora derivamos. Derivada de constante é zero e a a gente deriva usando a regra da Potência (ou regra do Tombo)...
Essa subtração de fração no expoente a gente vai ter que colocar com frações de denominadores iguais, assim transformamos o em :
E então nossa derivada é:
Que a gente ainda pode jogar em forma de raiz e descer pro denominador (por causa do expoente negativo, a gente inverte):
Ufaa! Derivamos ! Agora vamos montar nossa Regra do Produto...
Passo 5
Voltando pra nossa derivada principal, vamos montar a regra do Produto, sendo:
Substituindo todo mundo:
E aí a gente pode fazer essas multiplicações, usando a distributiva (multiplica cada termo de um parênteses por cada termo do outro), pra deixar a derivada mais arrumadinha...
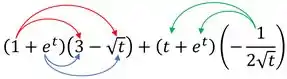
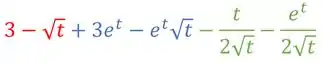
E pronto! Essa é a nossa derivada😉
Resposta
Exercício Resolvido #5
Seja
A derivada calculada para corresponde a:
(a)
(b)
(c)
(d)
(e)
Passo 1
Opa, galera, prestem atenção no enunciado, porque dessa vez não precisamos apenas derivar . Precisamos também substituir por depois que a gente derivar ! E o resultado dessa substituição é que será a resposta da questão!
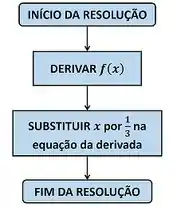
Esse é mais um exercício que o aparece em cima e embaixo da divisão! Sabemos que nesses exercícios, antes de começar a derivar uma função com divisão, temos que dar nomes para cada termo. Assim a gente se organiza melhor para quando for derivar.
Vamos chamar o termo de cima da fração de e o termo debaixo de .
Usando e podemos reescrever .
Mas como dar nomes ao termo de uma divisão pode organizar a resolução da questão?
Passo 2
Para derivar uma divisão, usamos uma regra chamada de regra do quociente.
A gente deu nome a cada parte da divisão no passo 1 para escrever a regra do quociente de um jeito mais fácil agora. Abaixo a gente pode ver a cara dessa regra.
Lembre-se que usamos o símbolo (chamado de apóstrofo) para representar as derivadas! Ou seja, é a derivada de , é a derivada de e é a derivada de !
Como e estão presentes na regra do quociente, precisamos calcular as derivadas de e para achar
Passo 3
Nesse passo, vamos calcular quanto vale a derivada de .
.Mas não precisamos derivar e ao mesmo tempo. Podemos calcular a derivada de cada um e só depois somar as duas para achar .
O e um número constante. Como a derivada de constantes vale zero, a derivada de um é nula!
Já para derivar usamos a regra do peteleco. Nessa regra, o expoente de leva um peteleco e cai na frente de . Além disso, o expoente deixa pra trás ele mesmo menos 1.
E qual é o expoente de para a gente aplicar essa regra?
é igual a . Isso quer dizer que seu expoente vale .
Logo, sua derivada é:
Somando as duas derivadas achamos quanto vale .
Passo 4
Nesse passo, temos que calcular quanto vale a derivada de .
, bem parecido com o de cima, né! Podemos, aqui também, calcular a derivada de e separadamente e só depois juntar as duas para achar .
No entanto, nós já calculamos quanto vale a derivada de e no passo anterior.
Juntando as duas derivadas achamos quanto vale .
Passo 5
Já temos tudo pra substituir na regra do quociente:
Agora vamos substituirpara calcular !
Ajustando as multiplicações:
Esse menos na frente do segundo parênteses altera o sinal de todo mundo que está lá dentro Assim, tirando os parênteses teremos:
Podemos cancelar o negativo com o positivo ficando com:
E já tá bonito. Mas calma, porque ainda não acabamos! Ainda temos que substituir o por ! Lembra?
Passo 6
Nesse passo vamos valcular o valor da derivada para . Para fazer isso, vamos substituir por na equação de que encontramos no passo anterior.
Para fazer a conta de , temos que colocar no mesmo denominador que .
Fazemos isso escrevendo o como . Podemos fazer isso porque . Assim:
Agora que os denominadores são iguais, nos resolvemos em cima e repetimos embaixo:
Substituindo esse valor na fórmula, achamos:
Aqui nós temos que elevar ao quadrado! Você se lembra como podemos fazer isso?
Para elevar uma fração ao quadrado, elevamos a parte de cima e a parte debaixo ao quadrado separadamente.
Substituindo isso na equação:
Útima coisa! Prometo!
Chegamos da divisão de por . Para fazer essa conta, mantemos o igual e multiplicamos ele pelo inverso de que vale .
E esse é o resultado final. Ou seja, agora é só marcar a letra (c) e comemorar!
Resposta
Letra (c).
Exercício Resolvido #6
Derive a função
Passo 1
Opaa! Vamos derivar essa função que é formada por um quociente entre polinômios. Pra isso a gente vai usar a regra do Quociente, que é dessa forma aqui:
Onde “” significa a derivada da função.
Vamos definir o que é o que nessa fórmula...
Passo 2
A gente pode ver a função dessa forma aqui:
E daí, podemos chamar:
e
Agora a gente derivar essas duas pra encontrar o e o que também aparecem na fórmula.
Passo 3
Vamos primeiro em ...
Isso aqui a gente já sabe derivar né? É só a gente derivar cada termo e manter a soma. Lembrando que derivada de constante é zero!
Beleza! Já derivamos ! Guarda isso por enquanto...
Passo 4
Vamos derivar agora! Da mesma forma que derivamos a , e pra isso vamos usar a regra do peteleco:
Prontinho! Derivada de encontrada com sucesso!
Passo 5
Bora montar nossa regra do Quociente agora:
Beleza! Agora a gente pode resolver essas multiplicações em cima pra ver se conseguimos simplificar alguma coisa!
Passo 6
Multiplicando em cima ali a gente tem:
Aqui podemos juntar todos os termos semelhantes, que são os que tem a mesma potência, vamos ficar com:
Como todos os termos que estão em cima são negativos, podemos colocar esse menos na frente da fração, e deixar em cima só o sinal de mais
E prontinho! Essa é a nossa derivada😉
Resposta
Exercício Resolvido #7
Considere a função . Indique qual a opção abaixo para .
(a)
(b)
(c)
(d)
(e)
Passo 1
Opa! Tudo joia? Olha só, a gente quer a derivada dessa função aqui:
Bom, aqui a gente tem um quociente de polinômios, certo? A gente usa então a Regra do Quociente, que é assim:
E no nosso caso:
Beleza? Vamos continuar...
Passo 2
A gente precisa das derivadas dessa ali. Vamos ver isso então:
Pra derivar essa, podemos usar a regra do Tombo nesses expoentes aí, tá lembrado? Essa aqui ó:
Aplicando isso em :
(derivada de constante é sempre zero😉)
Passo 3
Show! Vamos fazer a mesma coisa com :
Beleza! Agora que temos as derivadas de cima e de baixo, podemos montar nossa regra do quociente!
Passo 4
Substituindo tudo isso na fórmula:
Vamos aplicar a distributiva nessas multiplicações ali da parte de cima: 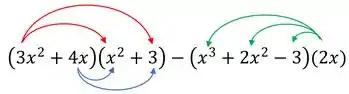
![]()
Então:
Juntando os termos semelhantes:
Essa é a derivada! Pra chegar na resposta de alguma daquelas alternativas,vamos ter que expantir aquele parênteses ali do denominador...
Passo 5
Vamos lá, você lembra o que é isso aqui?
É um produto notável dessa forma aqui:
Aplicando naquele caso aliesse produto notável ao nosso caso:
Beleza! Expandimos os parênteses, vamos substituir na derivada agora!
Passo 6
Voltando aqui:
Substituímos:
E assim chegamos na resposta da letra 😊
Resposta
(d)
Exercício Resolvido #8
Se onde e , encontre
Passo 1
Fala aí! Ficou confuso com essa história de ?
Calma... sem pânico! Vamos ver direitinho isso aí...
O que temos aqui é a multiplicação de por uma função que nós não conhecemos. Mas
Como é uma multiplicação, podemos aplicar a regra do Produto.
Lembra que a Regra do Produto é dessa forma aqui:
Aqui no nosso caso, temos:
Passo 2
Aí perceba que:
Então montando a derivada de , temos:
Beleza, essa é a derivada de . Vamos ver como podemos usar isso a nosso favor!
Passo 3
Veja que o enunciado nos deu:
E queremos . Vamos substituir na nossa expressão de então...
Substituindo o que nos deram e sabendo que :
Prontinho! Achamos o valor de que nos pediram😉
Viu como ela nem foi tão cabulosa assim pra resolver? rsrs
Resposta
Exercício Resolvido #9
Encontre e .
Passo 1
Olá! Vamos ver mais essa derivada aqui?
Devemos achar a primeira derivada e a segunda derivada da função .
Repare que a função é um produto entre o e o , então podemos usar a regra do Produto.
Pra lembrar, a regra do produto é assim:
Passo 2
Pra usar essa regra temos que definir quem é e quem é . Podemos chamar assim:
Nós vamos precisar também das derivadas, e . Então, vamos derivar cada uma agora...
Passo 3
Pra derivar , vamos usar a regra do Tombo, que é assim:
Aplicando em , fica assim:
Precisamos fazer essa subtração com fração ali no denominador. Mas pra isso, as frações precisam ter o mesmo denominador, então vamos escrever o como sendo .
Como as frações agora ficaram como o mesmo denominador, podemos subtrair em cima e repetir embaixo e ficará assim:
Beleza, derivamos !
Passo 4
A nossa é uma exponencial, olha só:
A derivada da exponencial é a própria exponencial, ou seja:
Show! Bora montar nossa regra do produto então!
Passo 5
Sendo: , , e
Encontramos uma soma entre dois termos e nos dois aparece o , então podemos colocar ele em evidência na frente dos parênteses:
Prontinho! Essa é a primeira derivada! Vamos ver a outra?
Passo 6
Para acharmos , calculamos a derivada de . Pra isso vamos usar a regra do produto de novo, do mesmo jeitinho que fizemos ali em cima...
Vamos nomear novamente nossas funções chamando:
e vamos derivar e .
Passo 7
A derivada de é a própria , assim:
Agora , será feita com a regra do tombo também:
Beleza, mais uma derivada pronta!
Passo 8
Vamos substituir essas derivadas na nossa regra do produto:
Colocando o em evidência:
E pronto! Essa é a segunda derivada de .
Calculamos então ! 😊
Resposta
e
Exercício Resolvido #10
Encontre e .
Passo 1
Opa! Vamos ver mais essa derivada aqui😊
Queremos encontrar e dado .
Como a gente tem duas um quociente de funções sendo divididas, vamos usar a regra do Quociente, que é assim:
Onde aqui a gente pode chamar:
Passo 2
Vamos precisamos fazer as derivadas de e agora:
Para , vamos lembrarlembrando da regra do tombo:
E pra , vamos lembrar que a derivada de uma constante é zero, e a derivada da exponencial é ela mesma:
Beleza! Já temos tudo que precisávamos. Vamos montar a Regra do Quociente agora!
Passo 3
Substituindo...
Multiplicando ali em cima:
Pronto! Essa é a primeira derivada!
Passo 4
Vamos pra segunda derivada agora! A gente vai usar a regra do quociente de novo, vamos derivar essa aqui:
Vamos calcular cada derivada dessas então...
Passo 5
Essa aqui primeiro:
Aqui a gente tem uma constante, uma exponencial e um produto. Vamos derivar cada pedacinho:
Vamos ver esse pedacinho aqui: . Aqui temos um produto, então a gente aplica a regra do produto:
Juntando tudo, nossa derivada de é:
Beleza! Essa já foi... vamos pra !
Passo 6
Agora vamos pra essa aqui:
Vamos reescrever assim:
Aqui vamos aplicar a Regra do Produto:
Prontinho! Mais uma derivada pronta! Vamos jogar isso tudo na regra do Quociente agora...
Passo 7
Pra relembrar: a gente achou:
Vamos substituir isso aqui agora:
Ficou feio né? Vamos dar uma resolvida nessas multiplicações ali pra ver se fica melhor. Repara que temos dois grandes termos no denominador, e que o está nos dois::
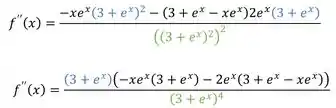
Também resolvemos a parte do denominador que possuía uma potência de uma potência, então repetimos a base e multiplicamos o expoente.
Repara agora que temos , multiplicando e dividindo, então podemos cortar um de cima com um de baixo, ficando com:
Agora vamos resolver as multiplicações do numerador:
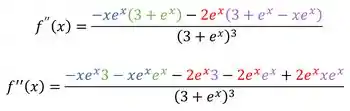
Organizado:
Agora, podemos juntar os temos que forem semelhantes:
![]()
E... finalmente chegamos em !
Prontinho! Calculamos 😊