Introdução e Propriedades das Derivadas
Teoria
Introdução
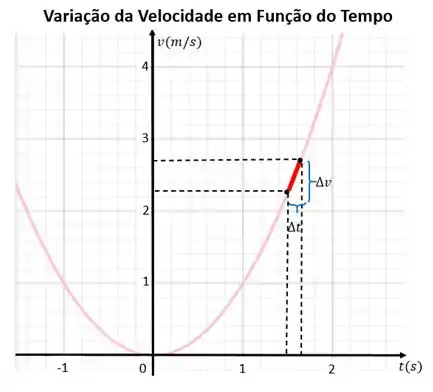
Faaala aí galera! Vamos falar um pouco sobre variações? Show, então vamos olhar um gráfico que mostra a variação da velocidade de um móvel com o passar do tempo:

A pergunta aqui é a seguinte: Qual foi a variação da velocidade desse móvel, por unidade de tempo, desde até ?
Para descobrir isso nós olhamos no gráfico e podemos ver que quando , a velocidade do móvel era igual a .
E para a velocidade já era igual a .
Então a velocidade variou em , dentro desses segundos.
Mas o que foi perguntado foi a variação por unidade de tempo. Sendo assim, temos que calcular quanto a velocidade variou a cada segundo. Fazemos isso, dividindo a variação da velocidade pela variação do tempo (vamos representar essa variação com o símbolo ):
Agora sim, temos a variação por unidade de tempo, que foi de . Essa variação pode ser representada no gráfico pela reta vermelha:
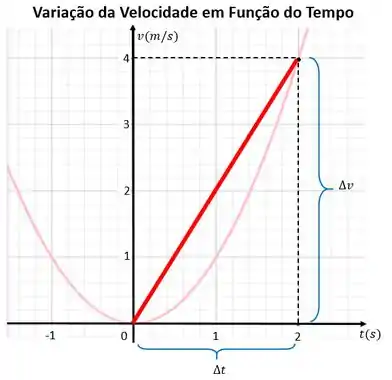
Mas você concorda que essa variação não foi a mesma em todos os momentos? Porque veja, o gráfico a partir do ponto começa a crescer devagarinho e depois vai crescendo cada vez mais rápido. O que nos mostra que mais pra cima a variação foi mais rápida que no início.
Podemos ver isso se fizermos a variação para intervalos menores, veja:
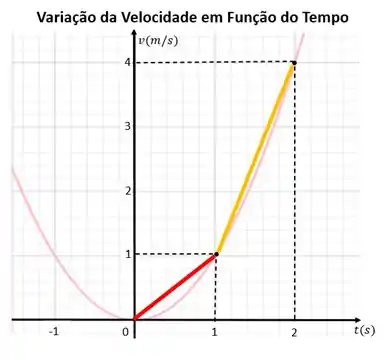
A linha laranja é maior e mais inclinada porque a velocidade aumentou de para , uma variação de . Já a linha vermelha é curtinha e menos inclinada, pois a velocidade aumento de para apenas .
O que acontecerá se pegarmos intervalos de tempo cada vez menores para observar essa variação?
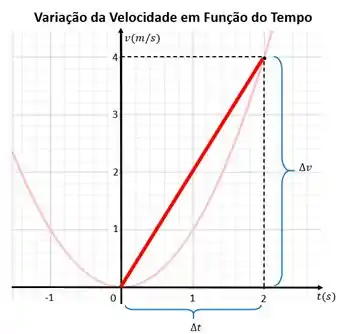
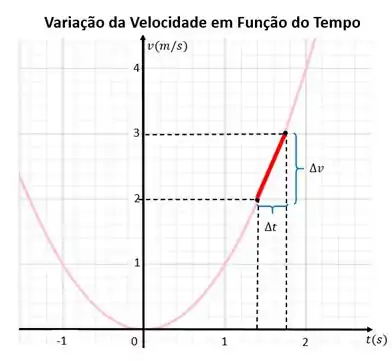
Bem, quanto menor for o intervalo de tempo, mais próximo da variação instantânea nós estaremos. E é assim que a gente vai definir uma nova ferramenta chamada derivada.
A derivada diz pra gente qual a taxa de variação de uma função. Ou seja, a variação a cada instante de tempo.
Como o intervalo é muito pequeno aquele que estávamos usando antes se transformará apenas em . Então, a taxa de variação passa de:
E ela será definida dessa maneira aqui:
Calma, calma, calma! Na grande maioria dos casos você não vai precisar resolver esse limite não, ok?
Essa é apenas a definição formal para calcular a taxa de variação de uma função qualquer. Que na realidade é a mesma coisa que já fizemos ali em cima com a variação da velocidade.
Veja, na parte de cima temos:
Que diz o quanto a função mudou de um ponto pra outro. E na parte de baixo temos o
Que diz em qual intervalo estamos analisando essa mudança da função.
Por fim, o
Está ali porque queremos saber qual a taxa de variação instantânea da nossa função, então fazemos o intervalo ser bem pequeno tendendo a zero.
Mas como eu disse, serão poucas as vezes que vamos mesmo ter que resolver uma derivada usando esse cálculo, porém o entendimento do que é a derivada vai ajudar bastante a gente em nossa caminhada pelo cálculo.
 a
a
Relaxa e vem comigo porque agora vamos aonde realmente importa!!!
Como calcular uma derivada:
Resolvendo aquele limite ali em cima, você consegue encontrar a derivada de qualquer função. Mas o grande “barato” é que as funções que são do mesmo tipo, maravilhosamente respeitam as mesmas regras de derivação. Isso vai ajudar muuuuuuiiitoo a gente, porque pelo tipo de função, já poderemos saber como será a sua derivada. Vamos ver algumas delas:
- Derivada de uma função constante:
- Derivada de polinômio:
- Multiplicação por constante:
- Somas e subtrações:
Vimos que a derivada representa a taxa de variação. Se temos uma função constante, quer dizer que ela NÃO VARIA, então a derivada dela só pode ser igual a ZERO!
Também podemos representar a derivada usando . Essa que está em cima da função, vai dizer pra gente que essa é a derivada da função .
Assim, se:
Se:
Se:
E assim, por diante... Seja qual for o valor da constante, sua derivada sempre será igual a ZERO!
Quando nossa função for uma potência de , para encontrar a derivada, o expoente leva um “peteleco” e caí na frente do multiplicando. Quando ele cai, ele perde uma unidade no expoente:

Assim, se:
Quem está no lugar do é o número . Assim o caí pra frente do multiplicando e perde uma unidade no expoente, então:
Vamos ver outros exemplos:
Se:
Se:
Eita! Cadê o expoente desse ?
ATENÇÃO! Quando a potência não tem expoente, significa que esse expoente é igual a 1. Então pode colocar o 1 lá em cima e derivar normalmente:
Aí, a gente precisa lembrar que todo número elevado a zero é igual a 1. Assim:
Vamos pra mais uma:
Opaaaa!!! E agora? Pode estar no denominador “produção”???
ATENÇÃO! Primeiro a gente precisa subir essa potência para o numerador. Fazemos isso colocando o sinal de menos no lugar do expoente. Então:
Agora sim, aplicamos a regra:
Essas funções são as principais que a gente precisa saber pra começar com o pé direito. À medida que formos avançando iremos conhecer algumas outras. Mas por enquanto vamos dar uma boa treinada com essas que já é meio caminho andado.
Propriedades de Derivação:
Nossas funções podem vir acompanhadas, então algumas propriedades podem ser usadas na hora de derivar. Vejamos quais são elas:
Pra derivar uma função que possui uma constante sendo multiplicada, nós mantemos a constante e derivamos apenas a função:
Assim:
O está multiplicando o , então nós mantemos o multiplicando e derivamos o , ficando com:
Outro exemplo, se:
Primeiro jogamos o que está no denominador, para o lado de cima, colocando um sinal de menos no expoente:
Agora vemos que o 2/3 está multiplicando, mantemos ele e derivamos o , ficando com:
Pra derivar esses carinhas aí, a gente vai fazer a derivada de cada um separadamente olhando termo a termo:
Assim,
Essa regra é bem tranquila, deriva cada pedacinho com calma que não vai ter problema.
Derivada de um ponto
Imagina que você se depara com a seguinte pergunta:
Qual a taxa de variação da função quando o ?
O que queremos saber nesse caso é o quanto a função está variando instantaneamente em um ponto específico. Então a gente faz primeiro a derivada da função e depois a gente substitui o valor de por na nova função que encontrarmos.
Veja:
Qual a taxa de variação da velocidade de um objeto que se desloca com , no instante ?
Ahh, nesse caso a variável é o e não o , mas as regras são as mesmas, só mudamos as letras.
Vamos primeiro deriva:
Agora a gente substitui o valor de por . Ficando com:
E agora resolve:
Assim a taxa de variação no instante é de .
Derivada de Ordem Maior que 1
Ordem? Calma é mais fácil que parece, vou explicar: Seja a função a derivada vai ser:
Podemos derivá-la novamente:
Quantas vezes eu derivei a função original? né? Então essa é a derivada de ordem.
Se eu quiser agora a derivada de ordem dessa ? É só derivar de novo:
Posso fazer isso eternamente. Repara que a ordem nada mais é que a quantidade de vezes que derivamos essa função. Então, se eu quiser a ordem eu preciso ir derivando vezes até chegar na que ele quer.
Eu preciso ficar escrevendo esses milhões de tracinhos com milhões de parêntese? Não, não. A notação das derivadas de ordem superior é parecida com as de antes
Até a ordem você coloca tracinhos, mas tudo junto. A partir da ordem só colocar o número ali junto da função entre parênteses.
Outra forma de escrever é
Coloca o número da ordem com o elevado, e embaixo coloca o elevado a isso.
Legal, né? Vimos bastante coisa hoje. E depois de aprendermos tudo isso, pra ficar “fera” nesse assunto, é só praticar com bastante exercício que vai ficar no sangue!
Então, PARTIU EXERCÍCIOS :D
Como calcular uma derivada:
Propriedades de Derivação:
Derivada de um ponto
Derivada de Ordem Maior que 1
Exercícios Resolvidos
Exercício Resolvido #1
Se qual é a única resposta correta para a sua primeira derivada?
Passo 1
Fala! Empolgada(o) para fazer exercícios de derivada? Fica tranquilo, porque aqui você vai entender tudo com um passo a passo bem explicadinho!
O primeiro passo é entender o enunciado! O que ele quer saber quando pergunta qual é a única resposta correta para a derivada da função abaixo?
Essa é só uma forma diferente de te pedir para derivar! O enunciado quis dizer: qual é a derivada desse em relação a ?
Representamos a derivada de em relação a como .
Como , achamos:
E por que ele pediu a primeira derivada? O que isso quer dizer? Existe a segunda derivada?
Quando ele pede a primeira derivada de , ele pede que você derive apenas uma vez! Se você derivasse duas vezes seguidas, você encontraria a segunda derivada de . Essa segunda derivada é representada da forma abaixo.
O número indica que essa é a derivada!
Mas não vamos perder o foco! Temos que resolver esse exercício e até agora só entendemos o enunciado! Então vamos fazer isso no próximo passo.
Passo 2
Para entender como derivar uma função com termos somados ou subtraídos, como é o caso da função , temos primeiro que lembrar como derivar cada termo separadamente!
Então, vamos olhar pra cada item da função, a começar pelo . Vamos nos lembrar como se deriva a constante presente em !
Derivar é a mesma coisa que calcular a taxa de variação! Então para que exista uma derivada é preciso que a função esteja variando. Mas se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Ou seja, como não varia em relação a , sua derivada vale .
Agora vamos olhar o termo presente em lá do início da questão? Como calculamos ele?
Passo 3
Calculamos a derivada de , usando a regra do peteleco! Essa regra é usada para derivar variáveis (como a variável ) que estão elevadas a uma constante! No nosso caso, temos que lembrar que a variável está elevada a !
Isso quer dizer que esse termo está elevado a uma constante. Logo, podemos usar a tal regra do peteleco!
Essa regra diz que, quando derivamos um termo elevado a uma constante , o expoente do termo “cai pra frente da função” e passa a multiplicar. Além disso, quando ele “cai pra frente da função, ele perde uma unidade”, ou seja, passa a ter um novo expoente !

No nosso caso, o expoente vale . Ao perder essa unidade, ficará no novo expoente. Assim:
Mas todo número elevado a zero é igual a . Então:
Pronto! Achamos a derivada de cada termo! Mas quanto vale a derivada de completo?
Veremos isso no próximo passo!
Passo 4
Nos passos anteriores vimos quanto vale a derivada de e a derivada de . Porém, ainda não vimos quanto vale a derivada total de !
Para calcular a derivada total, precisamos adaptar a regra de derivada da soma! Vimos que a derivada da soma é igual à soma das derivadas! Agora veremos que:
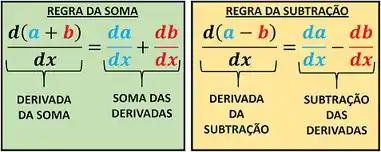
Ou seja, a derivada da subtração é a subtração das derivadas!
Aplicando isso em , encontramos sua derivada .
Nos já calculamos e ! Substituindo o que encontramos:
Resumindo, vale:
Aeeeee! Terminamos o exercício de derivadas! Esse passo a passo ajudou? Responde aí!
Resposta
Exercício Resolvido #2
A derivada da função é:
Passo 1
Vamos desvendar o que essa questão tá querendo da gente. Pra isso a gente precisa lembrar que termos somados e subtraídos podem ser olhados separadamente na hora de derivar, assim a nossa vida vai ficar muito mais fácil!
A derivada de pode ser reescrita como abaixo.
Onde vamos fazer a derivada de cala parcela separadamente:
Está vendo? Sempre que tivermos uma função grande cheia de somas e subtrações, podemos derivar cada termo de forma separada e depois juntar tudo para calcular a derivada da função inteira!
Vamos fazer isso no próximo passo!
Passo 2
Para calcular as derivadas das variáveis elevadas a um expoente ( e ), usaremos a regra do peteleco! Essa regra diz que, quando derivamos um termo elevado a uma constante , o expoente do termo “cai” e passa a multiplicar. Além disso, passa a ter um novo expoente !

No caso de , o expoente vale . então, esse expoente vai cair pra frente da função e passar a multiplicá-la. Ao cair ele perde uma unidade ficando:
E encontramos a primeira parte da nossa derivada.
Já no caso de , o expoente vale . Logo, vamos usar a mesma regra do peteleco ficando com:
Repara que nosso vai ficar elevado a zero, e todo número elevadoa zero é igual a . Assim:
Passo 3
O último passo é a cereja do bolo! Já fizemos todo o trabalho duro da questão! Agora é só juntar os resultados. Pra isso vamos lembrar como fizemos a separação lá no início:
Sendo e , teremos:
Não disse que o último passo era só um detalhe pra fechar com chave de ouro a nossa questão?
Pode comemorar! Fizemos mais um exercício de derivada!
Resposta
Exercício Resolvido #3
A derivada da função é:
(a)
(b)
(c)
(d)
(e)
Passo 1
E aí, se assustou com essa função cheia de termos diferentes (, e )? Eu também! Mas sempre que eu olho uma questão de derivada que me assusta muito, eu respiro fundo e lembro que deve existir um jeito mais simples de enxergar a questão!
Nesse caso, , e estão presentes na função para representar valores constantes, então eles são na verdade números que estão ali!
Ou seja, , e têm o mesmo papel que o número teria na função .
Atenção! Não estou dizendo que , e valem . Estou apenas dizendo que esses três termos desempenham o mesmo papel na função que qualquer número desempenharia. Resumindo, , e representam números! Então vamos derivar tendo isso em mente!

Além disso, a gente pode ver que as opções de resposta que temos têm um termo esquisito. Relaxa, esse termo é apenas uma outra forma de representar a derivada da função . Em outras palavras, e são formas equivalentes de se representar uma derivada.
Agora que entendemos o enunciado do exercício, podemos começar a derivar!
Passo 2
Essa função é a soma de vários termos. Podemos tirar proveito disso, usando uma propriedade da derivada. Essa propriedade diz que podemos derivar cada termo separadamente e depois juntar tudo de novo! Em outras palavras, podemos reescrever a derivada da soma com a soma das derivadas , e .
Sempre que a função for grande, cheia de somas e subtrações, podemos derivar cada termo de forma separada e depois juntar tudo para calcular a derivada da função inteira!
Vamos derivar cada termo separadamente no próximo passo!
Passo 3
Para calcular as derivadas de e , usaremos a regra do peteleco! Nessa regra, a derivada faz o expoente “cair” e passar a multiplicar o termo. Além disso, o expoente da derivada é o expoente antigo menos .
No termo , o expoente vai “cair” e passar a multiplicar. O novo expoente será .
Já no termo , o expoente de vale .
Isso quer dizer que o expoente vai “cair” e o novo expoente valerá .
Já sabemos o valor da derivada de dois termos. Falta só calcular a derivada de para juntar todos esses valores e encontrar a derivada total da função.
Passo 4
Derivar é a mesma coisa que calcular a taxa de variação! Se o termo não varia, como é o caso de uma constante, então sua taxa de variação vale zero!
Ou seja, como não varia em relação a , sua derivada vale .
Agora que já sabemos as derivadas de cada parcela, podemos substituir todos esses valores de derivadas na derivada total:
Como os resultados da questão representam a derivada de outra forma (com um ), vamos reescrever a equação acima para ficar mais clara qual é a resposta!
Essa resposta é a letra (e)! Agora é só marcar a opção (e) e correr pro abraço! Parabéns!
Resposta
Letra (e).
Exercício Resolvido #4
O valor de para é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Essa questão parece mais difícil do que as anteriores, mas na verdade é mais fácil. Vamos olhar bem a nossa função:
Antes de derivar, nós podemos facilitar a nossa vida separando essa fração esquisita em duas frações mais simples. Sempre que tivermos soma ou subtração no numerador, podemos separar dessa forma:
E ainda, como na segunda fração temos o em cima e em baixo, podemos simplificar ele, deixando assim:
Ficou bem mais bonita agora, né. O segredo é esse. Quando a gente se depara com algo que parece estar difícil, a gente tenda melhorar e simplificar ao máximo.
Passo 2
Agora, sim! Vamos derivar:
Lembra que, na derivada, podemos separar as somas e substrações? Vamos fazer isso:
Passo 3
Vamos começar derivando a primeira parte que é o . Aqui, pra facilitar a nossa vida, temos que lembrar que dividir por é a mesma coisa que multiplicar por . Olha só:
Agora, a derivada que sobrou envolve uma potência de multiplicada por uma constante. Já sabemos que podemos tirar a constante da derivada:
Vamos usar aquela a regrinha da derivada de potências de .
O seja, o 2 “cai pra frente multiplicando e perde uma unidade no expoente do ’. No nosso exercício, vai ficar assim:
Achamos a primeira.
Passo 4
Vamos olhar agora pro último termo que é o . Percebeu que esse é aquele caso onde temos uma constante multiplicada por ? Só que nesse caso, a constante é . A regrinha é a mesma que vimos antes. Olhando só o último termo agora:
Colocando o 1 na frente e no exponte do e derivando, teremos:
E todo número elevado a zero é igual a .
Assim a derivada do é:
Passo 5
Agora chegou a hora de juntarmos as duas informações que encontramos e montar a derivada:
Passo 6
Mas lembra que a questão pediu pra gente o valor de ? Isso significa que queremos saber o valor da derivada quando . Então agora só precisamos trocar o pelo na derivada que acabamos de resolver.
Vai ficar assim:
E agora? Como fazemos essa continha com frações? Pra fazermos somas e subtrações com frações, precisamos de denominadores iguais. Primeiro vamos lembrar que quando o denominador não aparece, é igual a .
Agora pra igualar os denominadores, vamos multiplicar a segunda fração por 3 em cima e embaixo.
Prontinho, os denominadores das duas agora valem . Agora podemos fazer as contas com os numeradores e repetir os denominadores.
Cosneguimos!
Resposta
Exercício Resolvido #5
Para uma epidemia em uma cidade, o setor de saúde indicou que o número de P pessoas infectadas no instante t (a partir do início da epidemia), pode ser descrito pela função entre os dias . Obter a taxa instantânea de variação quando
- 300
- 900
- 200
- 600
- Nenhuma das respostas anteriores
Passo 1
Fala galerinha, tudo tranquilo? Esse exercício quer que a gente calcule a taxa instantânea de variação da função , quando . Mas o que isso significa?
Sempre que um exercício pede para a gente calcular a taxa instantânea de variação de uma função, ele está querendo que a gente calcule a derivada dessa função!
Ou seja, a questão pede que a gente calcule a derivada de ! Mas não só isso! A questão pede que a gente calcule isso em um tempo específico . Então, depois de achar a derivada de , a questão ainda quer que a gente substitua o por !
Resumindo, precisamos derivar e depois substituir por na fórmula de derivada que encontramos!
Passo 2
Beleza, precisamos derivar fazendo:
Sempre que a gente quiser derivar uma função com somas e subtrações, podemos separar a derivada dessa função em derivadas menores, derivando cada termo. Então vamos derivar uma de cada vez:
Além disso, precisamos lembrar que as constantes não interferem na derivada. Isso significa que podemos tirar a constante de dentro da derivada.
Olha só que bacana! Conseguimos transformar aquela derivada maior em duas derivadas mais simples: uma derivada de e outra derivada de .
Vamos resolver elas no próximo passo!
Passo 3
e são potências de , ou seja, são elevado a uma constante. Sempre que a gente se deparar com uma potência, usaremos a regra do peteleco! Nessa regra, a derivada faz o expoente “cair” na frente de . Além disso, o expoente da derivada é o expoente antigo menos .
Por exemplo, no caso da derivada de , o expoente vai “cair” e o novo expoente será .
Agora é a vez do ! O expoente de vale . Logo, para a derivada de o expoente vai “cair” e o novo expoente será .
Substituindo essas derivadas que encontramos na equação da derivada grande, achamos:
Ainda podemos multiplicar por e assim chegar a nossa derivada:
Resumindo, a derivada de é igual a:
Mas lembra que a questão pede a derivada num tempo específico. Então, resta só substituir por nessa equação de derivada que encontramos.
Passo 4
Esse passo é mais tranquilinho que os outros! Precisamos apenas colocar o em todos os lugares que tiver na equação da derivada!
Para resolver essa conta, vamos primeiro começar com a potência, e temos que lembrar que é igual a . Depois a multiplicação de que é igual a .
Continuando a multiplicação:
Por fim:
Esse resultado mostra que a taxa instantânea de variação vale , quando ! Ou seja, a opção de resposta certa é a letra (b)!
Agora é só comemorar!
Resposta
Letra (b)
Exercício Resolvido #6
Certo corpo movimenta-se segundo a função horária de posição sendo x dimensionado em metros e t em segundos. Com base nessa informação, determine a velocidade instantânea sabendo-se que
Passo 1
Como o enunciado nos diz que a velocidade é derivada do espaço em relação ao tempo, então o que precisamos é fazer a derivada da função . Então, basta que resolvamos isso:
Vamos lembrar que temos a propriedade em relação a soma, onde podemos calcular a derivada de cada termo:
Passo 2
Bora lá analisar cada um então
Pra essa vamos fazer a regra do peteleco e mantamos o 2 ali na frente multiplicando, certo?
A próxima derivada vai ser no mesmo esquema da anterior, regrinha do peteleco e não mexemos na constante
O último é a derivada de uma constante, lembra que a derivada indica a variação e a constante não varia. Logo, a derivada dela é zero:
Agora juntamos tudo:
Resposta
Exercício Resolvido #7
Em certo planeta o espaço percorrido por qualquer objeto pode ser descrito pela função horária sendo o espaço em metros e o tempo em segundos. Determine a função horária que descreve a velocidade para esse tipo de função, lembrando que .
Passo 1
Beleza, lembra sempre do seguinte
Velocidade é a derivada do espaço. Como temos a função horária do espaço dada por:
Vamos ter que derivá-la para encontrar a velocidade instantânea.
E lembrar que temos a propriedade em relação a somas e subtrações, onde podemos calcular a derivada de cada termo
Passo 2
Bora lá analisar cada um então
Primeiro
Pra essa vamos fazer a regra do peteleco e mantemos o multiplicando, certo?
A próxima derivada vai ser no mesmo esquema da anterior, regrinha do peteleco e não mexemos na constante
Lembrando que todo número elevado a zero vale 1!
O último é a derivada de uma constante, que é zero
Resposta
Exercício Resolvido #8
Biólogos estão pesquisando que certa espécie de ave está ameaçada de extinção em virtude de comerciantes estarem usando as penas para brinquedos. Depois que várias medidas de preservação forem implementadas espera-se que a população de aves cresça de acordo com a regra:
Onde denota o tamanho da população ao fim do ano t. Calcule e interpretando os resultados.
Passo 1
O que o enunciado tá querendo da gente é esse e mas o que significam essas duas aspinhas aí em cima do ? Bom, quando elas aparecem significa que você precisa fazer a derivada de segunda ordem, que no final das contas é derivar duas vezes a função. Então, partiuuu!
Vamos derivar a primeira vez. Temos:
E podemos separar na soma das derivadas, certo?
Vamos aplicar nossas regras do peteleco em cada uma e lembrar que a derivada de constante é zero!
Essa é a primeira derivada. Agora vamos derivar a segunda vez, fica assim ó...
Repara que a gente vai pegar a primeira derivada e fazer a derivação dela novamente:
Facando:
Passo 2
No enunciado ele que valores específicos dessas derivadas quando ele pergunta quem é e Então, agora vamos encontrar os valores pedidos no enunciado substituindo os valores de .
Para t = 2, temos:
Para t = 8, temos:
Observamos que para e os cálculos revelam que no final do segundo ano a taxa de crescimento da população de aves aumentará uma razão de .
Ao final do oitavo ano a taxa estará aumentando a uma razão de . Conclui-se então que as medidas de preservação serão bem sucedidas se cumpridas.
Resposta
Exercício Resolvido #9
Determine os pontos de , nos quais as retas tangentes são horizontais.
Passo 1
Antes de tudo, precisamos lembrar que a derivada de uma função é representada pela inclinação da reta tangente ao gráfico daquela função em determinado ponto:

Como o enunciado tá dizendo que a reta tangente é horizontal, ela não terá inclinação e vai ficar tipo assim no gráfico:

Em outras palavras, a Derivada será igual a zero. E o que ele está querendo saber é qual é o ponto que faz isso acontecer. Repara que isso acontece quanto a função tem seus valores máximos e mínimos, também chamado de pontos críticos.
Então pra descobrir esses valores de , vamos precisar derivar essa nossa função e igualar a zero. Partiuuu!!!
Passo 2
Começamos pela derivada:
Lembra que temos a propriedade em relação a soma, onde podemos calcular a derivada de cada termo
Pra essa vamos fazer a regra do peteleco e não mexemos na constante, certo?
A próxima derivada vai ser no mesmo esquema da anterior, regrinha do peteleco e não mexemos na constante
O último é a derivada de uma constante, que é zero
Logo
Passo 3
Igualando a zero, teremos
Virou uma equação que podemos resolver isolando o , jogando o que está subtraindo, para o outro lado.
Agora é a vez de jogar o 3 que tá multiplicando, para o outro lado dividindo:
Temos:
Agora a pergunta é: Qual o valor que quando elevado ao quadrado dá 4?
Há duas possibilidades:
Porque ambos elevados ao quadrado resultam em
Passo 4
Agora vamos substituir esses valores na nossa função original
Primeiro para
Ou seja, o primeiro ponto é formado pelas coordenadas .
Agora vamos fazer para o
Ou seja, o segundo ponto é
Resposta
Exercício Resolvido #10
Uma carga de dinamite ao explodir lança uma pedra pesada para cima com uma velocidade de lançamento de . A altura da pedra pode ser descrita por , onde está em segundos e em metros. Qual a função que modela a aceleração da pedra em qualquer instante de tempo durante sua trajetória?
Passo 1
Beleza, vamos lembrar sempre do seguinte:
Aceleração é a segunda derivada do espaço.
Já que é a segunda, vamos derivar e derivar de novo. Então vamos lá derivar isso aí:
Lembrando que temos aquela propriedade em relação a soma, onde podemos calcular a derivada de cada termo.
Podemos fazer a regra do peteleco onde o expoente “cai pra frente do multiplicando e perde uma unidade”, certo?
Passo 2
Tranquilo até aí? Vamos agora derivar mais uma vez, lembrando que a derivada de constante vale zero.
Prontinho, agora pra fechar bonito vamos acrescentar a unidade de aceleração que é o .
Resposta
Exercício Resolvido #11
Com o uso de derivadas sucessivas podemos fazer interpretações da segunda derivada, com aplicações diretas na Física e Economia, por exemplo. Com isso, seja , para , a equação do movimento de uma partícula P com em metros e sem segundos. Utilizando a derivação sucessiva, determine a velocidade e a aceleração da partícula quando
Passo 1
Primeira coisa que precisamos nos lembrar é que a velocidade é a derivada do espaço...
Portanto, teremos o seguinte...
Lembra que temos a propriedade em relação a soma, onde podemos calcular a derivada de cada termo? Então:
Aplicando nossa regrinha do peteleco
Como ele pediu o valor da velocidade quando Vamos substitui o por na nossa função de velocidade. Fica assim ó:
Passo 2
Agora para determinarmos a aceleração vamos fazer a derivada da velocidade
Vamos lembrar que temos a propriedade em relação a soma novamente, onde podemos calcular a derivada de cada termo.
Aqui não precisaremos substituir o , pois a aceleração é constante e igual a . Então em qualquer momento ela será sempre igual a , inclusive no . É o que chamamos de movimento uniformemente variado, lá da Física.
Resposta
Exercício Resolvido #12
Em Pesquisa Operacional ou em Administração de Empresas é comum os cuidados com a otimização de processos, assim verifica-se que a função lucro da empresa ACÚSTIC é dada por dólares, onde x é o número de sistemas de som modelo F produzidos. Encontre onde a função é crescente e onde é decrescente.
Passo 1
O que o enunciado quer saber é, onde a função é crescente e onde é decrescente. Para isso precisamos lembrar da interpretação gráfica da derivada. A derivada é igual a inclinação da reta tangente ao gráfico. Vejamos um gráfico de uma função qualquer:
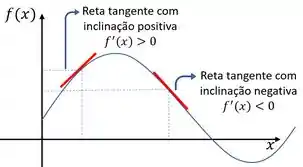
Repare que quando o gráfico da função é crescente (a curva está subindo), temos uma derivada positiva, e quando o gráfico da função é decrescente (a curva está descendo) a derivada é negativa. Então vamos usar essa informação aí pra matar essa questão.
Nossa função será:
CRESCENTE se
DECRESCENTE se
Então o primeiro passo é fazer a derivada de :
Observe o
Calculamos fazendo a derivada de cada termo:
Passo 2
Agora vamos ver em quais intervalos nossa derivada será positiva fazendo:
Bem, isso ai é uma inequação (porque tem aquele sinal de ali). Para resolver essa inequação, é bem parecido com resolver uma equação normal, vamos deixar o sozinho. Para isso vamos jogar o 300 que tá somando, para o outro lado subtraindo.
Agora tem um detalhe importante, o valor que acompanha o está negativo, para arrumar isso nós multiplicamos a inequação inteira por , e isso vai fazer com que todos os sinais se alterem, incluindo o sinal de (maior) que vai passar a ser (menor). Vai ficar assim ó:
Agora que o valor do já é positivo, vamos deixa-lo sozinho, passando esse 0,04 que está multiplicando, para o outro lado dividindo:
Isso significa que nossa função será crescente para todos os valores de que forem menores que 7500.
Passo 3
Agora vamos descobrir os valores onde a função será decrescente, lembrando que agora a derivada precisar ser negativa, ou seja, menor que zero.
Vamos deixar o sozinho aqui também:
E não se esqueça de multiplicar aqui por aqui também:
O que significa que nossa função será decrescente para valores de maiores que 7500.
A gente também pode confirmar isso olhando para o gráfico de :

Mas nem sempre temos o gráfico fácil a nossa mão, então a derivada ajuda a gente nessa tarefa aí.
Resposta
é crescente para
é decrescente para