Coeficientes Constantes Homogênea
Teoria
Introdução:
Faaaaala aí! Vamos dar prosseguimento ao estudo das EDO’s. Você lembra que já vimos como resolver EDO’s de 2ª ordem com coeficientes constantes homogênea? Se não, é só dar uma olhadinha na teoria, que tá tudo bem explicadinho pra você arrasar nessa teoria aqui também! Antes, estávamos tratando de equações desse tipo:
Beleza, agora imagina que tenhamos isso:
A única diferença é que temos derivadas de ordem maior que dois envolvidas.
Como que faremos pra resolver isso? Você vai ver que é muito parecido com EDO de ordem.
Olha mais alguns exemplos do que vamos estudar nessa teoria:
Percebeu alguma semelhança em todas elas? Todas estão igualadas a ZERO e os coeficientes que acompanham e suas derivadas são NÚMEROS. Por isso, é chama de EDO Superior Homogênea com Coeficientes Constantes.
De maneira geral, as EDOs superiores homogêneas têm a seguinte cara:
Com todos , , constantes.
Como que faremos pra resolver isso? Você vai ver que é muito parecido com EDO de ordem.
Encontrando a equação auxiliar:
Pra começar, nada melhor que um exemplo né? Dá uma olhada:
Bom, a ideia aqui é a mesma de EDO de ordem, que seria pensar numa função cujas derivadas sejam bem parecidas com a própria função! Então, chutaremos de novo
Substituindo na EDO:
Maneiro! Temos um produto de duas parcelas sendo zero. Isso significa que ou uma é zero, ou a outra é. Porém, nunca é zero. Logo:
Aeeeee, chegamos num polinômio! Bora resolvê-lo :)
Encontramos nossas três raízes. Vamos escrever as soluções assim, ó:
Podemos agora escrever a solução geral, que vai ser sempre a soma de todos os :
MUITO SHOW! Vamos generalizar?
Dada uma EDO desse tipo:
Montaremos a equação auxiliar:
Encontraremos as raízes da equação e para cada uma delas teremos um . Por fim, escrevemos a solução geral:
Beleza... Agora preciso te dar uma notícia meio chata. Quando temos uma equação de grau devemos ter raízes, o detalhe que não necessariamente temos raízes diferentes, basta que as multiplicidades das raízes somem . Como nós estamos tratando de polinômios, temos que ter em mente que algumas raízes podem ter multiplicidade maior que um (reais ou complexas) :/ Vamos ver cada caso?
Raízes com multiplicidade 1:
Bom, se tem multiplicidade um, temos que ver o caso em que ela é real e o caso em que ela é complexa:
- Se a raiz for real, a solução é dada por
- Se a raiz for complexa, então
Quando temos uma raiz complexa dessa forma podemos garantir que vamos ter uma outra raiz complexa que vai ser
E a solução dessas duas juntas vai ser
Olha um exemplo com raízes complexas:
Começamos com a equação auxiliar
Colocando em evidência:
Isso nos dá que
Todas essas raízes apareceram uma vez só, então tem multiplicidade .
Para , que é uma raiz real, temos
Para , que é complexa, temos
Então a solução geral vai ser:
Raízes com multiplicidade maior que 1:
Imagina que temos duas raízes e iguais (chamaremos ambas de )! A solução de cada uma será:
Entendeu a ideia? Você vai multiplicar a solução pela variável até que ela fique diferente das outras. E se forem quatro raízes iguais?
Sacou? Olha um exemplo:
Começamos com a equação auxiliar:
Mas repara que , então
Isso nos diz que:
Da primeira temos . Esse só tá aí pra você ver que são duas raízes iguais.
Da segunda, tiramos que
Isso é só pra você ver que:
O que nos dá
E as nossas raízes são
Repara que tem uma galera aí com multiplicidade . Agora vamos escrever a solução. Para :
Para :
Então a solução geral vai ser:
Dá trabalho, mas praticando tudo dá certo!
Tá... Mas e na hora de encontrar as raízes, como faço?
Relaxa, vou te ensinar um método muito bom.
Método de Briot-Ruffini
Exemplo: Vamos encontrar a solução geral da EDO abaixo.
A equação auxiliar é:
Como encontrar as raízes dessa equação?!
O detalhe nesse método é que você só pode usá-lo se você conhecer uma raiz. Então, o que a gente faz é ver os candidatos a serem raízes.
Qual o coeficiente do maior grau dessa equação? Neste caso vai ser , vamos chamar isso de
Qual o valor do cara sem a variável ? Vai ser , vamos chamar isso de
As possíveis raízes vão ser os divisores de sobre os divisores de , lembrando que para cada possibilidade vamos ter o cara podendo ser positivo ou negativo.
Nesse caso, os divisores de são . Os divisores de são . Logo, as possíveis raízes são
Então temos que testar essas raízes na equação, como fazemos isso? É só substituir o valor na equação e ver se vai dar . Se der , o valor de é raiz, e se não der , ele não é raiz.
Vamos começar testando
Portanto, é raiz.
Agora que temos uma raiz dessa equação, podemos aplicar o método de Briot-Ruffini para diminuir essa equação em grau. Você lembra como é esse método? Primeiro vamos colocar a nossa equação aqui embaixo:
A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem. No nosso caso, todos os graus estão presente na equação.
Agora montamos o seguinte quadrinho:
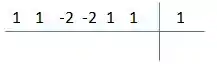
No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz.
Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar:
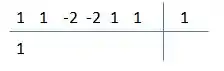
O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.
Nesse caso fazemos
Esse primeiro nessa equação imediatamente acima é o coeficiente, o segundo é o número do canto superior direito e aquele outro é o próximo coeficiente.
Fazendo essa conta chegamos ao valor , colocamos esse valor embaixo do coeficiente , ficando:
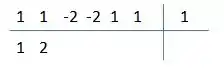
Agora é só repetir, a nossa conta dessa vez vai ficar:
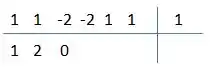
Agora é só repetir, a nossa conta dessa vez vai ficar:
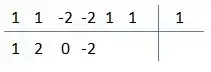
Agora é só repetir, a nossa conta dessa vez vai ficar:
Agora é só repetir, a nossa conta dessa vez vai ficar:
Como aquele último cara deu , a nossa conta está certinha. Se não der alguma conta está errada.
A nossa nova equação vai ser aquela que tem os coeficientes de baixo, tirando aquele , começando com um grau a menos do que o anterior. Neste caso, vamos ter:
Se você repetir todo esse processo a quantidade de vezes necessárias, vai encontrar as raízes que faltam. Eu já fiz e te digo que são:
Beleza, agora que temos todas as raízes podemos achar a solução geral dessa EDO!
Repare que temos uma raiz com multiplicidade e outra com multiplicidade , então a solução para cada raiz vai ser:
E a nossa solução geral vai ser:
Que vai ficar
Finalmente matamos essa questão!!!
Partiu exercícios!
Raízes com multiplicidade 1:
Raízes com multiplicidade maior que 1:
Método de Briot-Ruffini
Exercícios Resolvidos
Exercício Resolvido #1
UFF - Cálculo IIA - P2 Sérgio Licanic 2014.1 – 5
Determine a solução geral da equação diferencial
Passo 1
Vamos fazer o mesmo que fazíamos para equações de ordem 2. Resolver a equação característica.
Temos que tentar achar uma soluçaõ e reduzir o grau da equação. Somando os coeficientes percebemos que o resultado é zero, isso significa que o número é solução da equação. Logo ela pode ser reescrita como
Aqui vamos ter
Então
Vamos as outras raízes
Passo 2
Seguindo a analogia das EDO’s de ordem 2 a solução será
E é exatamente assim que fazemos com EDO’s lineares de coeficientes constantes com ordem maior do que dois.
Resposta
Exercício Resolvido #2
UERJ - Cálculo 3 - Lista 4 Fernando Lopes - 2b
Resolva a seguinte equação:
Passo 1
Bom, na nossa teoria vimos que a equação característica será:
Essa é uma equação biquadrada a solução é sempre criar variável chamada: e substituir ela nessa equação:
Passo 2
Encontrar , e :
Passo 3
Verificar discriminante: , ou ?
Passo 4
Encontrar raízes da equação auxiliar:
Cálculo das raízes:
Opa, mas então temos que:
Passo 5
Po, se antes com duas raízes eram duas funções exponenciais, agora que temos 4 raízes de multiplicidade 1 com determinante maior que zero, adivinha?? Vão ser a soma de 4 exponenciais!
Encontrar a solução:
Substituindo os valores de :
Resposta
Exercício Resolvido #3
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 8ª ed., Rio de Janeiro: LTC, 2010, pp. 125, exercício 17
Encontre a solução geral da equação diferencial dada.
Passo 1
Bem aqui temos uma EDO homogênea, isso porque temos a EDO igual a .
A primeira coisa a fazer é achar a equação característica
Primeiro vamos dividir todo mundo por para diminuir nossas contas
Agora precisamos achar as soluções de equação. A primeira coisa que fazemos numa equação assim é ver se temos algum para colocar em evidência, e neste caso não temos isso
Temos que resolver
Passo 2
Vamos ver algumas dicas de como resolver uma equação de grau maior que . A ideia é ir achando as raízes aos poucos e ir diminuindo o grau dessa equação.
Quando temos uma equação assim temos alguns candidatos a raízes dessa parada.
Qual o coeficiente do maior grau dessa equação? Neste caso vai ser , vamos chamar isso de
Qual o valor do cara sem a variável ? Vai ser , vamos chamar isso de
As possíveis raízes vão ser os divisores de sobre os divisores de , lembrando que para cada possibilidade vamos ter o cara podendo ser positivo ou negativo.
Os divisores de são e os divisores de são e , assim as possíveis raízes vão ser
Então temos que testar essas duas raízes na equação, como fazemos isso? É só substituir o valor na equação e ver se vai dar , se der o valor de é raiz, se não der ele não é raiz.
Vamos começar testando
Substituindo na equação vamos ter
Como deu , é uma raiz dessa equação. Então vamos ter
Passo 3
Agora que temos uma raiz dessa equação podemos aplicar o método de briot-ruffini para diminuir essa equação em grau. Você lembra como é esse método? Primeiro vamos colocar a nossa equação aqui embaixo
A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem, neste caso a equação já está completa.
Agora montamos o seguinte quadrinho
No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz.
Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar
O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.
Nesse caso fazemos
Esse primeiro é o coeficiente, o segundo é o número no canto superior direito e aquele é o próximo coeficiente.
Vamos achar , colocamos esse valor embaixo do coeficiente , ficando
Agora é só repetir, a nossa conta dessa vez vai ficar
E vamos ter
Agora é só repetir, a nossa conta dessa vez vai ficar
Como aquele último cara deu a nossa conta está certinha, se não der alguma conta está errada.
A nossa nova equação vai ser aquela que tem os coeficientes de baixo, tirando aquele , começando com um grau a menor que o anterior, neste caso vamos ter
Como achamos uma equação de grau podemos fazer como fazemos normalmente. Se essa equação tivesse grau maior que era só fazer tudo que acabamos de fazer de novo para diminuir o grau dessa equação
Passo 4
A nossa equação vai ser
Então temos todas as raízes agora, vamos escrever essas raízes aqui
Passo 5
Beleza agora que temos todas as raízes podemos achar a solução geral dessa EDO.
Todas as nossas raízes tem multiplicidade então nossas soluções vão ser
E a nossa solução geral vai ser
Que vai ficar
Resposta
Exercício Resolvido #4
UERJ - Cálculo 3 - Lista 4 Fernando Lopes - 2e
Exercício nº 2 letra e lista 6 de Cálculo III – IME - UERJ – Prof. Fernando Lopes C. -2014
Encontre a solução do problema de valor inicial abaixo:
Passo 1
Temos aqui um problema que envolve uma derivada de ordem:
Só que conseguimos melhorar nossa situação usando uma parada muito útil! Vamos usar a substituição simples de início:
-Substituindo:
Eita, isso é uma EDO de segunda ordem homogênea, no estilão que costumamos resolver!
Temos, então
Passo 2
Verificar discriminante: , ou ?
Passo 3
Encontrar raízes da equação auxiliar:
Cálculo das raízes:
Passo 4
Encontrar a solução:
Mas sabemos que
Logo:
Uma Edo separável!!
Como resolver essa integral??
Tem que fazer duas integrações por partes:
E novamente:
Notou que as duas integrais são iguais?! Pois é! Vamos ajeitar essa equação!
Passando a integral pro lado esquerdo:
A outra integral é exatamente o mesmo procedimento para resolver! Essa dará:
Logo finalmente:
Não importa muito como ficam as constantes que multiplicam o seno e o cosseno, porque elas são determinadas pelas condições iniciais, assim podemos trocar isso por outra constante:
Outro exercício bem diferente, né? Bastante trabalhoso por causa das integrais, mas foi um ótimo treino, você está vendo tudo quanto é tipo de exercício diferente!