Curvas Compostas
Teoria
Curvas Compostas
Existem alguns problemas que a nossa região vai ter “furos”, por exemplo
Sendo:
Obs: Note que o campo nas duas integrais é o mesmo! O esboço dessas curvas é esse aqui
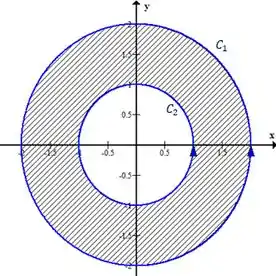
Como podemos usar o teorema de Green?
O bom do teorema de Green é que, mesmo nesse caso em que temos uma curva composta, o teorema é válido! Vamos ter que tomar cuidado somente com a orientação das curvas.
Todas as curvas, olhando uma por uma, têm que estar orientadas positivamente. Ou seja, a região tem que ficar à esquerda quando percorremos a curva. Dá uma olhada nessa figura aqui comigo:
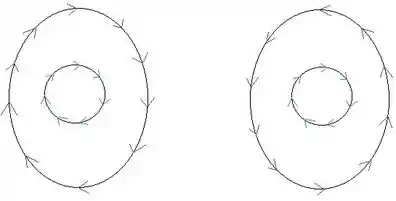
A primeira figura não está orientada positivamente. Note que, se andarmos sobre a curva de fora, a região fica à direita! Já na segunda figura, quando percorremos em ambas as curvas, a região de interesse fica à esquerda. Percebeu a diferença?
Depois de garantir tudo isso e considerando , o teorema fica assim
De volta ao problema
Perceba então que já temos um problema: nossa curva composta não está orientada positivamente! A curva precisa ser invertida, fazemos isso desse jeito aqui
Graficamente, agora ficou certinho, vê só
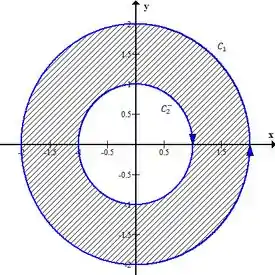
Agora sim! Com uma curva composta orientada positivamente podemos usar o teorema de Green, fica assim
Sendo a região entre as duas curvas. Beleza, agora é só calcular a integral dupla!
Vamos começar calculando
O que é consideravelmente simples, então não devemos ter problemas para calcular a integral.
Vamos jogar o valor na fórmula:
Para esse caso, o domínio é bom para ser escrito em coordenadas polares, então:
Substituindo isso na integral dupla
Resumindo o passo-a-passo, então:
Passo 1: Montar o problema
Passo 2: Calcular
Passo 3: Calcular a integral dupla
Agora, vamos aos exercícios praticar isso aí!
Como podemos usar o teorema de Green?
De volta ao problema
Exercícios Resolvidos
Exercício Resolvido #1
UERJ - Análise Vetorial - Lista 3 Flávio - 4f
Calcule , utilizando o Teorema de Green, onde e é a fronteira da região limitada por e , orientada positivamente.
Passo 1
Primeiro, vamos fazer um esboço da curva. Como o enunciado fala, temos duas cincunferências, uma de raio e outra de raio .
A região limitada pelas curvas é essa coroa, entre o círculo vermelho e o azul.
Cuidado com a orientação da curva, lembre-se do seguinte: para a curva estar orientada positivamente, andando sobre ela, temos que ver a região que ela limita à nossa esquerda. Para a curva de fora, isso significa sentido anti-horário, para a de dentro, sentido horário. Essa é uma condição fundamental para aplicarmos o Teorema de Green!
Passo 2
Beleza, agora precisamos calcular :
Passo 3
Agora podemos montar a integral. Aplicando o teorema de Green, a integral do enunciado pode ser escrita como:
Onde é a região que vimos no passo .
Passo 4
Como a região está compreendida entre duas circunferências, a melhor saída aqui são as coordenadas polares. Faremos:
Pelo próprio gráfico, vemos que , o que equivale a uma volta na circunferência. Os valores de variam entre as duas curvas, logo . Temos, então:
Não se esqueça desse da mudança para coordenadas polares!
Passo 5
Agora vamos resolver isso aí, integrando em relação a temos:
Agora em relação a :
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule para o campo onde é a curva orientada no sentido positivo e composta por
Passo 1
Vamos lá, galera, essa curva é composta por vários pedaços, vamos juntar tudo em um esboço pra ver como fica
Aparentemente aqui podemos usar o teorema de Green, né? O teorema é esse aqui, onde é a fronteira da região .
No nosso caso, a região é aquela sombreada ali no esboço. Precisamos primeiro encontrar esse termo e delimitar a região , depois é só integrar.
Passo 2
Vamos começar calculando
Substituindo lá em cima
Voltando para o teorema de Green, ficamos com
Portanto só precisamos descobrir a área da região ! Ela vai ser a área da parábola menos a área da circunferência, vamos fazer cada uma delas separadamente
Passo 3
A área da parábola deve ser feita pela integral dupla mesmo, os limites vão ser esses aqui
Essa é a área da parábola, certo? Precisamos retirar aquele círculo desse valor! A área do círculo é definida por
A circunferência é descrita por , portanto o seu raio é igual a , com isso
E a área total pode ser escrita como
Passo 4
Voltando para o resultado que encontramos pelo teorema de Green
Resposta
Exercício Resolvido #3
UFF - Cálculo IIIA - Lista 4, GMA 2015.2 – 25
Seja
Calcule a integral de linha do campo ao longo de e , orientadas no sentido anti-horário, onde
Passo 1
Vamos começar achando a integral de linha de , para isso precisamos parametrizar , como é uma circunferência de centro e raio vamos ter
Com
Passo 2
Precisamos agora da derivada dessa parametrização
Passo 3
A integral vai ficar
Lembrando que
Passo 4
Vamos ver agora a integral de , repara que antes conseguimos fazer direto porque na função aparece a equação de dessa vez não vai aparecer se tentarmos fazer na “marra” vai aparecer uma integral surrealmente louca. Vamos marotamente usar o teorema de Green agora, mas temos um problema, a função não está definida em , vamos colocar a região para o teorema de Green sendo a região de fronteira onde assim tiramos o nosso problema, o detalhe que vamos ter
Dessa vez vamos ter
Eu coloquei esse porque a orientação da curva deve ser ao contrário agora, porque elas devem rodar em sentidos contrários, ou seja, deve ser horário, e o que achamos no passo foi no sentido anti-horário.
Então
Passo 5
Vamos agora calcular :
Passo 6
Aplicando o teorema de Green, temos:
A área de é a área da circunferência de raio menos a área da circunferência de raio . Então:
Passo 7
A integral de linha vai ficar