Teorema de Green para Curvas Abertas
Produzido por Arthur Melo de AlmeidaTeoria
Teorema de Green para Curvas Abertas
Como você faria essa integral aqui? Onde é a metade superior da circunferência de raio e centro na origem que liga até
Não se esquenta, ela é praticamente impossível de se fazer com a definição normal de integral de linha. Mas dá uma olha no termo desse campo aí
Parece super tranquilo de usar o teorema de Green aqui, não é? O empecilho é que a curva está aberta, como resolvemos isso então?
O macete aqui é fechar a curva com outra curva simples de integrar (de preferência uma reta que seja constante em ou ). Olha só como fica esse aqui se fecharmos com a reta que liga as extremidades da curva
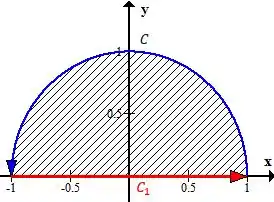
“Mas pode fazer isso? Não vai mudar o resultado da integral, não? ”
Pra usar esse macete, a gente vai ter que “corrigir” o valor da integral, o teorema de Green diz isso aqui
Para curvas abertas, vamos considerar , dessa forma
Ou seja, conseguimos calcular uma integral de linha complexa, ou quase impossível, com uma integral de linha e uma integral dupla simples.
Só um detalhe importante: lembre-se que, ao acrescentar uma nova curva, temos que garantir que que a curva fechada terá a orientação positiva para aplicarmos o teorema.
De Volta ao Problema
Voltando pra nossa integral de linha bizarra, olha só como fica no final das contas. A curva que usamos para fechar é essa reta aqui
Portanto o teorema de Green fica assim
A integral de linha fica assim
A área da nossa região é metade da área do círculo de raio , portanto
Juntando tudo isso
Pra resumir o passo-a-passo:
Passo 1: Montar o problema
Passo 2: Fechar a curva
Passo 3: Calcular a integral dupla
Passo 4: Calcular a integral de linha da curva
Passo 5: Juntar tudo no teorema de Green
Vamos partir pros exercícios, temos várias formas de aparecer essas questões pra você, vamos lá?
De Volta ao Problema
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Cálculo 3 - P1 2013.2 – 4
Calcular a integral de linha da função vetorial
Ao longo da curva que liga o ponto ao ponto e é definida pela equação .
Passo 1
Essa integral de linha parece complicada de se calcular diretamente pela definição, não é? O campo vetorial envolve secantes, tangentes, termos não muito agradáveis de se trabalhar! Vamos tentar, então, aplicar o Teorema de Green e ver se encontramos algo mais simples.
A curva em que devemos integrar é uma semicircunferência, pois, elevando a equação ao quadrado, temos
Passo 2
Como deve ser maior que zero, queremos a parte de cima da circunferência de raio centrada em . Mas essa curva não é fechada, certo? Então vamos fechá-la na maneira mais simples: com um segmento de reta que liga seus pontos final e inicial.
A curva final será, portanto:
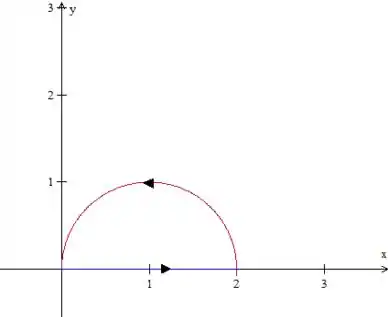
Veja que ela está orientada positivamente, não se esqueça disso!
Aplicando, então, o Teorema de Green, teremos, então:
Passo 3
Vamos agora calcular :
Passo 4
Aplicando o teorema de Green, temos:
Como se trata de uma semicircunferência de raio , temos:
Passo 5
Falta, agora, calcular a integral sobre o segmento , para isso, vamos parametrizá-lo. Como temos o ponto inicial e o final ligados pela reta , uma boa parametrização seria , onde temos ( é constante e varia).
Derivando essa expressão, temos
Passo 6
Montando a integral de linha sobre teremos:
Veja que escrevemos o campo em função da parametrização de .
Passo 7
Fazendo a diferença entre esses dois resultados, finalmente calculamos a integral sobre :
Resposta
Exercício Resolvido #2
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2004, pp. 229 ex. 6.8
Calcule , onde é o arco da circunferência , no primeiro quadrante, orientado no sentido anti-horário.
Passo 1
Vamos fazer um esboço da curva:
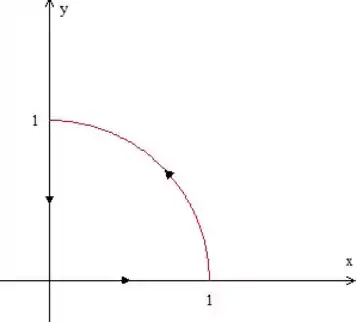
A parametrização desse arco envolveria senos e cossenos, que, quando substituídos na expressão do campo vetorial, tornariam a integral muito complicada. Vamos, então, aplicar o Teorema de Green aqui.
Passo 2
Perceba que a curva em que vamos integrar não é fechada, ela é composta apenas pelo arco de circunferência. O que faremos então? Vamos fechá-la, formando uma curva , onde é o segmento de reta horizontal e o vertical. Vamos orientar essa curva de positivamente.
Teremos, então:
Agora, vamos isolar o termo que queremos, :
Como os segmentos e são simples de parametrizar, vamos calculá-los pela definição mesmo.
Passo 3
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Sendo a fronteira da nossa região , aplicando o teorema de Green, temos:
Calma, essa ainda não é a resposta, ainda precisamos calcular a integral em e em . Guarde esse resultado.
Passo 4
Vamos parametrizar os segmentos e .
Para : Este é um segmento horizontal em que e varia, portanto, podemos parametrizá-lo assim: , onde varia de a .
Para : Este é um segmento vertical em que e varia, portanto, podemos parametrizá-lo assim: , onde varia de a .
Passo 5
Agora precisamos derivar essas parametrizações:
Passo 6
Substituindo esses valores na fórmula que vimos capítulo passado:
Temos:
Passo 7
O que queremos é a integral em . Temos que:
Substituindo os resultados que encontramos:
Resposta
Exercício Resolvido #3
USP - Cálculo 3 - P2 2010 – 3
Calcule , onde é a parte da curva contida no semiplano orientada no sentido anti-horário.
Passo 1
Bom, já deu para ver que calcular essa integral aí pela definição deve dar muito trabalho, né? Vamos tentar aplicar Green então. Temos:
Bom, como é uma expressão relativamente simples, quer dizer que estamos no caminho certo.
Passo 2
Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário e a região limitada por ela, temos:
Mas o problema pede a integral de linha na curva contida no semiplano . Ou seja, uma parábola com simetria em , que vai de a :
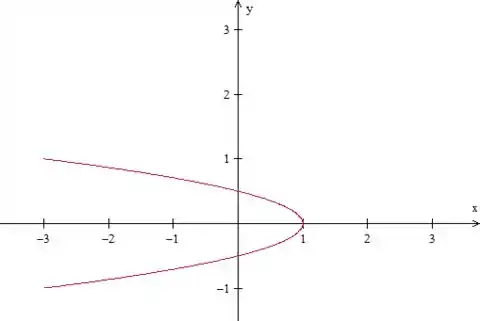
Logo, essa curva é aberta, precisamos fechar!
Então vamos fechá-la, com uma reta mesmo, que liga os pontos final e inicial, no mesmo sentido do arco:
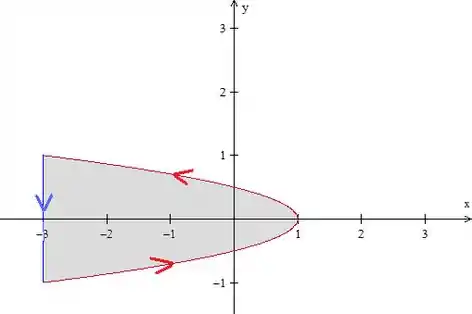
Então, sendo a união a parábola com a o segmento de reta orientados positivamente, temos:
Onde é a região em cinza na figura acima. Então, para encontrar a integral que queremos, precisamos resolver a integral dupla e a integral de linha na reta.
Passo 3
Vamos começar pela integral dupla. Descrevendo a região como tipo II, temos entre e e desde até , como podemos ver na figura. Levando para a integral, temos:
Passo 4
Agora vamos resolver a integral de linha no segmento de reta. Vamos começar parametrizando o segmento.
Como o segmento pertence à reta , podemos usar essa parametrização aqui:
Onde vai de a (por causa da orientação de ).
Agora vamos derivar essa parametrização:
Escrevendo o campo
Nas variáveis da parametrização, temos:
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Integral dá trabalho, né? Aqui, você pode pensar no seguinte: como essa função é ímpar (), o seu gráfico é espelhado em relação ao eixo , ou seja, toda a área que temos de a é igual à que temos de a , porém, uma integral terá sinal contrário à outra. Isso quer dizer que a integral de a será igual a zero! Logo:
Passo 5
Agora vamos substituir os valores que encontramos para calcular o que o problema pediu:
Resposta
Exercício Resolvido #4
USP - Cálculo 3 - P2 2012 - 3
Calcule para a curva com com ponto inicial e ponto final .
Passo 1
Bom, já deu para ver que calcular essa integral aí pela definição deve dar muito trabalho, né? Vamos tentar aplicar Green então. Temos:
Bom, como é uma expressão relativamente simples, quer dizer que estamos no caminho certo.
Passo 2
Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário, temos:
Mas o problema pede a integral de linha na curva (uma circunferência) com ponto inicial e ponto final . Logo, não temos uma volta completa na circunferência, essa curva é aberta.
Então vamos fechá-la, com uma reta mesmo, que liga os pontos final e inicial, no mesmo sentido do arco:
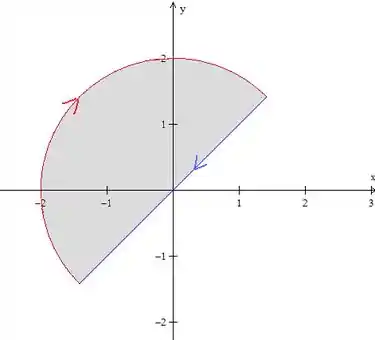
Então, sendo a união do arco com a o segmento de reta e estando sentido contrário (orientado negativamente), pelo Teorema de Green, temos:
Mas como:
E como queremos a integral de linha em , não :
Onde é a região em cinza na figura acima. Então, para encontrar a integral que queremos, precisamos resolver a integral dupla e a integral de linha na reta.
Passo 3
Vamos começar pela integral dupla. Já que temos um setor circular, vamos usar coordenadas polares:
Como vemos pela figura, (pois o raio da circunferência é ). O intervalo do ângulo , nós podemos ver por trigonometria: já que o ponto final é , sabemos que começa em . Pela figura, podemos ver que o ângulo final é , então, .
Fazendo a mudança polar então, temos:
Agora vamos resolver isso aí:
Passo 4
Para parametrizar a reta devemos primeiro notar que ela é escrita como
Fazendo , teremos a seguinte parametrização
Agora pela orientação temos que vai de até .
Escrevendo o campo
Nas variáveis da parametrização, temos:
Podemos, então, substituir os valores que encontramos na fórmula abaixo:
Passo 5
Agora vamos substituir os valores que encontramos para calcular o que o problema pediu:
Resposta
Exercício Resolvido #5
USP - Cálculo 3 - P2 2015 - 2
Calcule para a curva dada por com percorrida no sentido anti-horário.
Passo 1
Para escrever a curva na forma paramétrica teríamos que usar senos e cossenos, o que tornaria a integral muito complicada. Portanto, calcular essa integral pela definição não é uma boa. Vamos tentar usar o Teorema de Green aqui então.
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Essa é uma expressão simples, quer dizer que estamos no caminho certo!
Passo 2
Beleza, vamos aplicar Green então, mas em que região? Vamos primeiro descobrir quem é essa curva do enunciado:
Completando esses quadrados, temos:
A equação é uma circunferência de raio centrada em , certo?
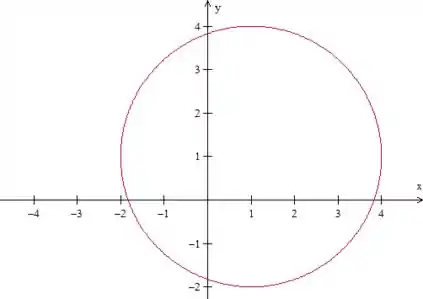
Como o problema diz que , temos isso aqui:
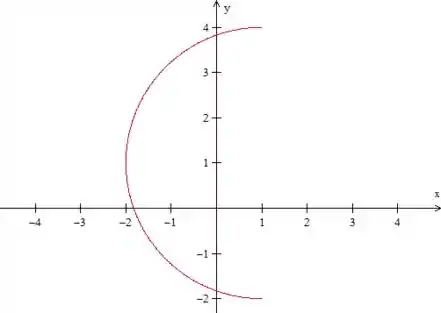
Mas para aplicar o Teorema de Geen, nós precisamos de uma curva fechada e orientada positivamente, não é? Vamos fechar isso aí com uma reta:
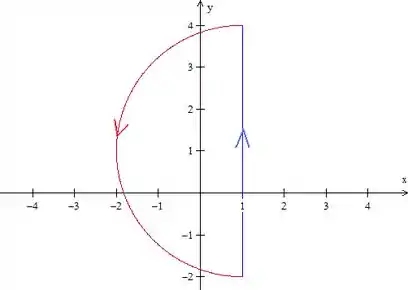
Como o enunciado já dizia que está orientada no sentido anti-horário, tá tudo ok então.
Agora podemos aplicar Green:
Onde é a reta do desenho e é a região entre o arco e a reta.
Passo 3
Como a região está compreendida entre um arco de circunferência e uma reta, a melhor saída aqui são as coordenadas polares. Faremos:
Esses termos que adicionamos na mudança polar estão aí porque a circunferência está deslocada da origem, lembra? Temos . Adicionando os termos , nós “levamos” o novo sistema de coordenadas para o centro da circunferência, que passa a ser escrita como .
Isso ocorre porque o da mudança polar faz desaparecer o da equação da circunferência, tornando sua equação .
Bom, sabemos então que . Como temos meia volta da circunferência, olhando para o gráfico e lembrando que o novo eixo de coordenadas está no seu centro, vemos que .
Agora, fazendo a mudança polar na integral, temos:
Passo 4
Agora precisamos parametrizar essa reta que criamos.
Temos um segmento que pertence à reta (para qualquer ), portanto, podemos parametrizá-lo assim:
Pela figura, vemos que .
Agora vamos substituir esses valores na fórmula:
Aplicando a parametrização na expressão do campo:
A integral fica:
Passo 5
Agora vamos encontrar o que queremos: