Integrais de Funções Básicas
Teoria
Fala aí. Nesse tópico vamos abrir nossas cabecinhas pra aprender como fazer a Integração de várias funções que vamos esbarrar por aí. Então bora começar.
Os principais tipos de funções que vamos encontrar para integrar são:
- Integral de Função Constante:
- Integral de Função Polinomial:
- Integral de :
- Integral de :
- Integral de Funções Trigonométricas:
Você se lembra o que acontecia quando a gente derivava uma função desse tipo aqui:
Bom a derivada dela é:
O desaparece sobrando só o como derivada. Como na integral estamos fazendo o processo inverso da derivação, ao integrar uma função constante, vamos devolver o que ela perdeu na derivada. Assim:
Veja outros exemplos:
E assim por diante...
É só dá um de presente para a constante, e não esquecer de colocar nossa constante de integração no final.
Assim como na derivação, para integrar uma potência temos uma regra específica que diz que a integral será a potência acrescida de uma unidade no expoente e dividida pelo novo expoente. Assim:
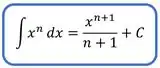
Sem dúvidas, essa é uma das principais regras de integração, e não vale esquecer a constante , hem.
Vamos ver um exemplo:
Veja que quem está no lugar do é o expoente 5. Então, aplicando a regra da integração de potência, teremos:
E se a potência estiver no denominador, também pode? Assim:
Bom nessa caso, você primeiro sobe a potência para o numerador colocando o expoente com o sinal trocado, e aí sim você faz a integração. Assim:
Então podemos fazer a integração com essa regra a quase todas as potências, a única exceção será a função . Veremos ela agora:
No caso da integral de , para aplicarmos a regra do expoente, teremos que subir o com o expoente negativo, que se tornará . Aplicando a regra:
O que não pode acontecer, uma vez que ficaríamos com uma divisão por zero. Então, aqui teremos que pensar: qual a função que quando eu derivo resulta me ? Bom, a resposta é o . Assim:
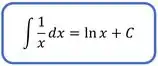
Assim, a integral de é o .
Cuidado com essa aqui viu, a gente costuma usar bastante ela. Fica a dica.
E por falar em logaritmo neperiano, você se lembra do ? Lembra que a derivada dele era ele mesmo? Então a integral de é igual a ela mesma também. Veja:
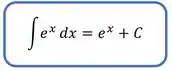
Com isso, o que podemos perceber é que existe uma regra pra cada tipo de função. Assim, o ideal é reconhecer primeiro qual o tipo de função que estamos integrando e depois ver qual a regra que se encaixa.
Algumas funções bem comuns que vão aparecer em exercícios são as funções trigonométricas. Vamos dar uma olhadinha nelas também.
Para funções trigonométricas, vamos sempre pensar no processo de antiderivação para encontrar a integral. Assim o jeito é fazer o caminho inverso, perguntando qual a função que quando derivada resulta na função que estamos querendo integrar.
Você se lembra da nossa tabelinha de derivadas trigonométricas? Era essa aqui:

Vamos construir outra dessa, mas agora com o processo inverso, que é a integral de funções trigonométricas. Vai ficar assim:

Viu, exatamente o inverso da derivada!
Ainda temos outras três integrais que são um pouco mais difíceis de deduzir, mas que também são importantes de saber, são elas:
Pronto, com todas essas integrais que vimos, você já será capaz de fazer muitos exercícios.
Então PARTIU para os exercícios pra treinar bastante. Te vejo lá!!!
Exercícios Resolvidos
Exercício Resolvido #1
Calcule a integral definida
- e³ - e
- 1 – e
- 2
- e
- 2e
Passo 1
Pessoal, o exercício quer que a gente calcule uma integral que ele chama de integral definida. Mas o que é uma integral definida? E o que são esses numerozinhos em cima e embaixo da integral?
Bem, esses numerozinhos são chamados de limites de integração. Quando uma integral tem esses limites de integração, ela é chamada de integral definida!
Mas relaxa, porque nesse início de resolução a gente não vai usar os limites de integração!
No início, vamos integrar normalmente a função como se eles não estivessem ali. Só não esquece totalmente deles porque vamos usá-lo no final, tá!
Vamos calcular a integral de Mas o que é essa letra “” da integral?
A letra “” é uma constante bastante usada em cálculo e física, que vale aproximadamente .
Vai ser comum vermos ela por aqui. Mas fica tranquilo, porque não vamos precisar usar esse valor de “” nas questões. Nós podemos deixar o próprio , só lembrando que é uma constante de valor específico!
Então vamos fazer essa integração no passo seguinte!
Passo 2
Então vamos começar integrando o !
Integrar o é muito tranquilo, porque a integral de é o próprio ! Logo:
Mas essa aí é a solução de uma integral indefinida, e por isso precisamos colocar sempre esse no final.
Mas espera! Lembra que nossa integral é definida, porque tinha aqueles limites de integração?
Então o certo é escrevermos dessa forma aqui:
Ao resolver uma integral definida, não precisamos colocar a constante de integração , mas temos que colocar essa barrinha com os limites de integração após a solução da nossa integral pra lembrar que ainda precisamos usá-los de alguma forma.
Então vamos fazer isso no próximo passo!
Passo 3
Finalmente vamos usar os limites de integração!
Pra isso vamos reescrever nosso resultado e substituindo o pelos limites de integração! Vamos fazer isso com cada um dos limites. Primeiro o que está lá em cima (o ), e depois o que está na parte de baixo (o 1) e vamos subtrair os resultados das nossas substituição.

Esse aí é o chamado “Teorema Fundamental do Cálculo”. Lembre-se sempre de fazer nessa ordem, primeiro o de cima e depois o de baixo.
Usando essa regra, a expressão vira:
No entanto, quando temos um número elevado a , podemos esconder o expoente.
Substituindo isso na integral, achamos:
Ou seja, a resposta certa é a letra (a). Ponto pra gente!
Resposta
Letra (a)
Exercício Resolvido #2
Ache a integral indefinida geral.
Passo 1
Beleza, temos que calcular quanto vale essa integral grandona e cheia de somas!
Quando a função que está dentro da integral é cheia de somas e subtrações, a gente tem que lembrar que podemos separar a integral grande em várias pequenininhas. Olha só como a integral fica:
Desse jeito, a gente substituiu uma integral grande mais complicada por várias integrais mais simples!
No próximo passo a gente vai ver como calcular cada integral!
Passo 2
Vamos começar a integrar, resolvendo a integral mais simples. A integral mais simples é a integral da constante . Sempre que tem uma constante sozinha dentro de uma integral, nós temos que dar para ela um de presente!
Só que o é igual ao próprio .
As duas integrais que restaram serão calculadas no próximo passo.
Passo 3
Primeiro de tudo, é importante lembrarmos que as constantes não vão interferir na integral. Então, podemos colocar essas constantes (que no caso é o ) fora da integral.
Também precisamos lembrar que, quando o não está elevado a nenhum número, ele está na verdade elevado a .
Substituindo isso na integral, ela vira:
Desse jeito fica melhor de perceber que as integrais que restaram são potências de .
Pra nossa sorte, existe uma regrinha bem simples que vai ajudar a encontrar rapidinho a integral de qualquer potência de elevada a um valor . A regrinha é: soma no expoente e divide pela soma que você acabou de fazer nesse expoente. Ou seja, a regrinha geral, ficaria assim:
Para usar essa regra, nós temos que lembrar que o expoente de vale e que o expoente de vale !
Usando essa regra, as integrais restantes vão ficar assim:
Resolvendo as continhas, temos:
Então acabamos o exercício, certo?
Nããão! Calma aí! Não se apresse! Antes de terminar tudo, ainda temos um passo para cumprir! Esse passo é muito importante. Se você esquecer dele, pode acabar perdendo pontos preciosos em provas.
Passo 4
No último passo, nós temos que lembrar de somar uma constante genérica no final da integral! Essa constante pode valer , , ou . Tanto faz o valor dessa constante. O que importa é que ela tem que estar presente na integral! Para indicar que essa constante pode ter qualquer valor, vamos chamar ela de e vamos somar esse no fim da integral!
Pronto, agora terminamos, não é?
Não hahaha mas eu prometo que essa é a última surpresa!
Tá vendo que o está sendo multiplicado por e dividido por ? Para deixar nossa resposta bem organizada, temos que dividir o pelo !
Agora sim a nossa resposta está pronta! Com essa resposta dá pra tirar um !
Resposta
Exercício Resolvido #3
Calcule a integral.
Passo 1
Opa! Vamos fazer mais essa?
Primeiramente, vamos obter a integral indefinida da função, esquece os limites de integração por enquanto...
Como existem dois termos ali (o e o ), a gente pode separar assim:
E resolver cada uma separadamente...
Passo 2
Essa aqui primeiro:
Repara que a gente ainda pode retirar o de dentro da integral e colocar ele pra frente já que é uma constante:
E aí essa integral é de um polinômio já que o pode ser escrito como , então a gente usa essa regrinha aqui:
Não esquece do que está ali na frente hem!. Aí a nossa fica:
Resolvendo essas somas de , teremos:
Como está multiplicando e dividindo por , podemos cancelar o de cima com o de baixo, e finalmente ficará assim:
Beleza! Essa já foi!
Passo 3
A outra integral é essa:
Essa é mais fácil ainda! Integral da exponencial é a própria exponencial! Ou seja:
Show! Vamos juntar as duas partes agora😊
Passo 4
(esse é a constante, já que ainda estamos na integral indefinida)
Agora que já calculamos a integral indefinida, vamos aplicar os intervalos nela!
Jogamos esse fora e colocamos a barrinha com os limites de integração no final, na mesma ordem que está na integral.
Passo 5
Pelo Teorema Fundamental do Cálculo, a gente aplica esses limites da seguinte forma: substituímos os limites de integração, um de cada vez no lugar do no resultado da integral. Então, fazemos o resultado do limite de cima menos o resultado do limite de baixo. Então vai ficar assim:
![]()
Vamos ter que resolver essas continhas aí. Então vamos olhar cada uma com cuidado.
Primeira: Zero elevado a qualquer valor é sempre igual a zero.
Segunda: Qualquer número elevado a zero é sempre igual a um.
Terceira: Potência com a base negativa , olhamos o expoente , se ele for par, dá positivo, e se for ímpar dá negativo.
Quarta: Quando o expoente é negativo, invertemos a fração, que no caso do pra deixar ele positivo.
Agora a gente junta tudo.
E prontinho! Esse é o resultado da nossa integral definida😉
Resposta
Exercício Resolvido #4
Calcule a integral.
Passo 1
Galera, o exercício quer que a gente calcule uma integral que tem esses numerozinhos em cima e em baixo dela. O que eles são?
Esses numerozinhos são chamados de limites de integração.
Quando uma integral tem esses limites de integração, ela é chamada de integral definida!
Mas relaxa, porque nesse início de resolução a gente não vai usar os limites de integração!
Antes, temos que lembrar que tirar a raiz quadrada é a mesma coisa que elevar a ! Olha só:
Além disso, elevar dois números juntos é a mesma coisa que elevar cada número separadamente!
Substituindo isso na integral, encontramos:
Essa integral está pronta pra ser calculada! No próximo passo a gente vai integrar!
Passo 2
Primeiro, nós temos lembrar que a as constantes não interferem na integral e podem ser tiradas de dentro dela. é uma constante. O fato de ela estar elevada a um número, não muda o fato de ela ser uma constante.
Colocando pra fora da integral, achamos:
Agora só sobrou o elevado a !
Sempre que tivermos elevado a um número, podemos usar uma regrinha.
A regrinha é: soma no expoente e divide por esse resultado. Ou seja, a regrinha geral, ficaria assim:
Para usar essa regra, nós temos que lembrar que o expoente de vale . Logo:
Para fazer essa conta, precisamos reescrever o que está sozinho no mesmo denominador que a fração . Para isso, vamos transformar ele na fração . Podemos fazer isso porque , então não alteramos o valor do e teremos frações com o mesmo denominador pra somar!
Na hora de somar frações, depois de deixar elas com o mesmo valor no denominador, é só somar os números de cima e repetir o de baixo:
Substituindo isso na integral, achamos:
Note que os limites de integração ainda estão presentes para lembrar que eles ainda precisam ser usados. Não vamos usá-los agora, mas é importante deixa-los aí!
Vamos só arrumar melhor nossa resposta.
Quando dividimos um número por uma fração, nós podemos multiplicar a parte de cima pelo inverso da fração. A parte de cima é o . O inverso da fração vale . Com isso, temos que:
Outra coisa que podemos fazer, é reescrever essas potências que tem fração no expoente, em forma de raízes. Pra isso vamos usar a regra abaixo:

Então o
E o
Escrevendo dessa maneira, fica um pouquinho melhor pra entender. E nossa integral se torna:
Agora só falta aprender a usar os limites de integração. No próximo passo a gente faz isso!
Passo 3
Finalmente vamos usar os limites de integração!
Fazemos isso, substituindo o pelos dois limites! Em outras palavras, nós vamos trocar os por um limite de cada vez. Primeiro, nós vamos trocar o pelo limite de cima (pelo ) e depois vamos trocar pelo limite debaixo (pelo ). A regra de troca do é mostrada abaixo.
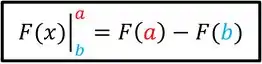
Usando essa regra, a expressão vira:
Nós podemos tirar o termo com da equação pra deixar um pouco mais simples, já que , e como ele está multiplicando o , essa parte inteirinha vai sumir, sobrando só:
Vamos fazer esse cálculo no último passo!
Passo 4
Para resolver essa conta vamos começar pela . Quando existe uma potência dentro da raiz a gente pode jogar ela pra fora da raiz, resolver a raiz só do que sobrou, e depois a gente resolve a potência. Assim ó:
Show, agora a gente encaixa isso no resultado da nossa integral:
Dividindo o por e multiplicando por , vamos ficar com:
Enfim achamos quanto vale a integral do enunciado! Show!
Resposta
Exercício Resolvido #5
Considere a integral indefinida descrita pela função f a seguir
Podemos afirmar que o valor da função f calculada para x = 1 é igual a:
Passo 1
Show, vamos resolver mais essa integral!
Temos isso daqui:
A primeira coisa que vamos fazer, é separar esse nosso problema em partes menores, da seguinte forma:
Tudo que for constante a gente coloca para fora. Mas atenção! Pra gente colocar o da primeira integral pra fora, não podemos deixar o sozinho perdido na parte de baixo. Por isso vamos deixar o no lugar desse . Assim:
Passo 2
Vamos lembrar de umas regrinhas agora:
Pra subir as potências que estão na parte de baixo, jogamos ela pra cima com o expoente negativo:
E as raízes podem ser escrita como potências também fazendo:
Shoow! Então a gente pode reescrever nossa integral assim:
Só não mexemos nesse ali do meio, porque pra ele a gente tem um valor todo especial.
A integral .
(a integral é tabelada😉)
E para integrar as potências a gente aplicar essa outra regrinha aqui:
Passo 3
Então vai ficar:
pra resolver aquela soma de frações ali no último termo, vamos escrever e aí somamos em cima e repetimos embaixo:
Essa fração na parte de não pode ficar aí, então invertemos ela e colocamos na frente multiplicando o .
simplificamos... e jogamos esse pra baixo, pra ficar com o expoente positivo:
Pronto! Já resolvemos o problema da integral!
Passo 4
Agora como queremos o valor para , então vamos substituir ali:
(Lembra que
Vamos transformar o em uma fração de denominador , multiplicando em cima e embaixo por :
Agora a gente resolve em cima e repete embaixo...
Prontinho! A resposta então é a letra 😉
Resposta
d)
Exercício Resolvido #6
Calcule a integral
Passo 1
Opa! Vamos ver mais essa aqui?
Olha só, quando a gente tem uma fração dentro de uma raiz, a gente pode separar os termos dela assim:
Bom, é constante, então a gente pode retirar pra fora da integral, mas pra não deixarmos o pedido na parte de baixo da fração, vamos colocar o 1 no lugar do :
Passo 2
Vamos agora deixar os limites de integração de lado só um pouquinho e calcular a integral indefinida:
Vamos precisar dessas regrinhas aqui agora:
Então na verdade a gente tem:
Passo 3
Agora a gente vai integrar por essa regrinha aqui:
Vamos ter:
Passo 4
Pra resolver aquela soma de frações ali, vamos escrever e aí somamos em cima e repetimos embaixo:
Isso aqui é o mesmo que:
Passo 5
Agora que já calculamos a integral indefinida, vamos jogar os limites de integração, lembrando que a gente faz o resultado do limite de cima menos o resultado do limite de baixo.
Ah, não esquece que a gente ainda tem aquela constante do lado de fora!
Aplicando então:
Prontinho! Calculamos a integral definida😉
Resposta
Exercício Resolvido #7
Calcule a integral.
Passo 1
Caraca, essa eu admito, feia pra caramba! Parece mega complicada, mas acredita em mim, não é!! Lembra de soma de fração? Olha isso
No nosso caso, observa que logo
Maravilha, olha como aquele cosseno dividido por cosseno da 1! Só facilita nossa vida. Além disso, podemos escrever o da primeira parte, como sendo .
A integral da secante ao quadrado é tabelada e vale tangente, e a integral de constante a gente só da um de presente
Não esquece da constante hein!!
Passo 2
Logo, pelo Teorema fundamental do Cálculo, a integral definida é:
Logo,
Resposta
Exercício Resolvido #8
Calcule a integral.
Passo 1
Bom pessoal , a primeira coisa que devemos fazer é separar as duas funções:
Temos que:
e
Obs: Essas duas integrais podem ser resolvidas com métodos específico de integração que veremos a frente, mas também tem resultados tabelados, que são os que mostrei acima. Seria legal você memorizar, mas se não conseguir, não se preocupa! Nos módulos da frente vou mostrar direitinho como resolver cada uma delas!
Passo 2
Agora, o próximo passo é aplicar o Teorema fundamental do Cálculo na integral definida:
Agora com:
Logo,
Resposta
Exercício Resolvido #9
Calcule a integral.
Passo 1
Ixiii, temos um módulo alí na função, mas calma, só precisamos analisar esse módulo e vai dar tudo certo.
Essas barras são chamadas de módulo. O termo da nossa função é lido como: “o módulo de ”.
E o que o módulo faz de diferente?
O módulo é o seguinte: caso o termo que estiver dentro do módulo seja negativo, o módulo o fará ficar positivo. Mas se o termo que está lá dentro já for positivo, o módulo o manterá positivo.
Mas como ele faz isso???? Vamos ver um exemplinho pra dar aquela clareada nas ideias. Para isso vamos usar outro valor qualquer, tipo o 5:
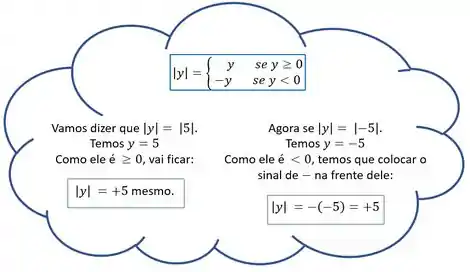
No nosso balazinho, o foi multiplicado por pra ficar positivo, por isso colocamos esse menos na frente dele.
Agora vamos ver como fica para o nosso exercício.
No nosso caso, o termo que está dentro do módulo é o . E saberemos que ele é negativo se ele for menor que zero.
Veja bem, para a nossa integral, como o intervalo de integração vai de a , e a função dentro do módulo é a função seno, olhando para o gráfico dela podemos ver que tem um pedaço dela que é positivo e outro que é negativo. O que teremos que fazer então, é dividir nossa integral em dois pedaços.
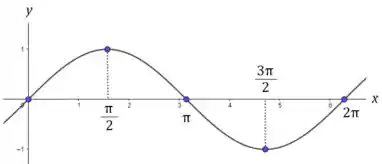
Veja como em a função deixa de ser positiva (ficar acima do eixo x) e passa a ser negativa (abaixo do eixo x). Faremos então o intervalo de integração de a temos que a função seno é positiva, então usamos , já no intervalo de a a função seno é negativa, assim (colocamos o menos na frente, por causa do lance do módulo), e vai ficar assim:
Viu? Agora fica simples de resolver, vamos lá!
Passo 2
Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:
Agora vamos achar as primitivas de cada função, usando duas expressões da Tabela de Integrais Indefinidas:
Agora é só aplicar, vamos resolver elas separadamente, assim fica mais simples de ver:
Para podemos colocar o do lado de fora da integral:
Passo 3
Pronto, já encontramos a integral indefinida, perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Ficamos então com:
Aaahhh, aqui não podemos cancelar o ) com o porque os limites de integração não diferentes tá!
Resposta
Exercício Resolvido #10
Supondo que uma função tenha derivada contínua para então o comprimento da parte do gráfico para é:
Calcule o comprimento do gráfico de de até
(a)
(b)
(c)
(d)
(e)
Passo 1
O enunciado pode tentar confundir a gente, mas aqui não tem segredo é só aplicar a fórmula que o enunciado deu.
Só que agora vamos usar a função no lugar dessa .
O primeiro passo é calcular a derivada da função, poque temos lá dentro da raiz
Parece complicado né? Vamos com calma. Primeiro tiramos a constante:
Agora vamos usar a regra da cadeia, chamando
E vazemos a derivada da de fora, vezes a derivada da de dentro.
Regra do petelecom para .
Resolvendo cada uma dessas derivadas:
E agora é só multiplicar tudo:
Passo 2
Agora vamos voltar para nossa fórmula:
Substituindo os valores, ficamos com a seguinte integral:
Admito, não ta com a cara bonita, mas tenha fé! Agora vamos elevar aquele parênteses de dentro ao quadrado, como é uma multiplicação do com o e com a, cada um desse carinhas vai ganhar o seu quadrado, ficando:
Já sumiu com uma raíz, o que é sempre lucro. Vamos agora fazer a multiplicação distributiva do . Multiplicando o por cada termo dos parênteses:
Agora é só resolver essa integral. Ta com a cara já bem mais tranquila, né?
Passo 3
Vamos começar reescrevendo esse polinômio para facilitar nossa vida. É preciso ter alguma intuição aqui:
Percebe que o primeiro e o último termo são quadrados perfeitos?
Isso tem cara de produto notável do tipo:
Veja que o está no lugar do , e que o está no lugar do .
Vamos ver se funciona:
Abrindo isso encontramos:
Ótimo, deu certo de primeira. Vamos colocar isso na integral:
Como é um quadrado dentro da raiz, podemos cancelar eles, ficando com:
Agora a integral desse polinômio é simples
Então substituindo os limites de integração:
Pronto! Esse é o comprimento do arco!
Resposta
Letra (a).
Exercício Resolvido #11
Elaboração Própria
A integral da função é igual a:
Passo 1
Vamos lá!! Queremos calcular o valor da integral indeterminada , certo?!

Então queremos calular
Como podemos calcular essa integral?? Vem comigoooo!
Passo 2
Pra começar, vamos relembrar como se calcula a integral de uma função polinomial! O que vai acontecer é
Ou seja, vamos somar 1 no expoente e esse número também irá para o denominador!
Beleza?!

Na prática, teremos
Show de bola?! Fazendo as somas, temos
Se você reparar, ainda podemos simplificar o numerador e o denominador
É muuuuito importante não esquecer de colocar o na resposta, pois temos uma integral indeterminada (não tem os limites de integração). Beleza?! Nesse caso, se não tiver o no final a resposta estará errada!