Substituição Simples
Produzido por Arthur Melo de AlmeidaTeoria
Opa! Bora aprender como resolver uma integral por substituição simples de uma vez por todas?
Como Resolver uma Integral por Substituição
Esse método de integração é um dos mais simples que a gente vai aprender, ele pode até ter uma cara feia inicialmente…mas com a prática você vai ver o quão tranquilo é e o quanto ele vai te salvar nas listas de exercícios! Então bora?
Imagina que você chega na sua prova e se depara com a seguinte integral:
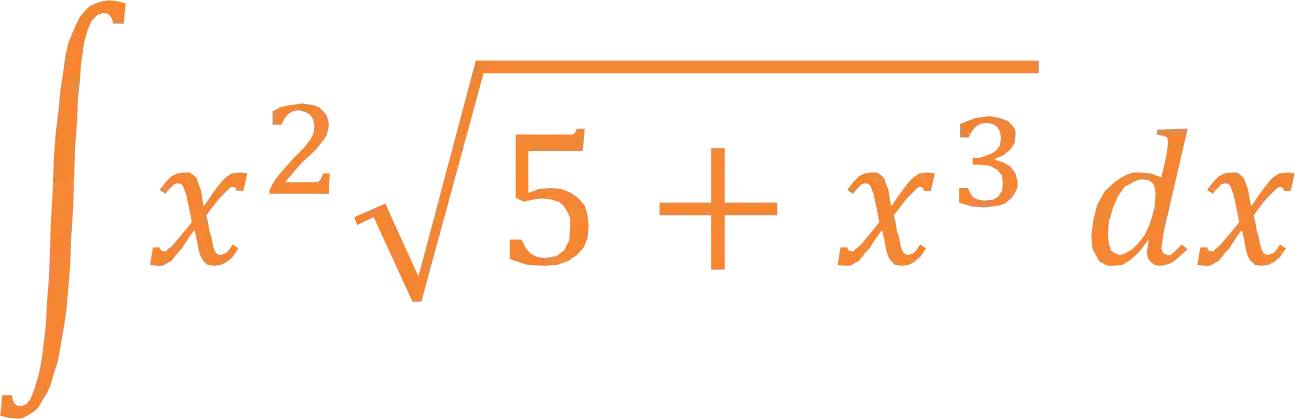
E ai, o que você faz? Se prepara que eu vou te dar o Passo a Passo para não ficar perdido quando tiver que resolver uma integral por substituição simples!
📢 Clique para ver mais:
Passo 1: Definir a Variável
Nesse método de derivação a gente vai fazer uma substituição de variável, ou seja, vamos trocar o
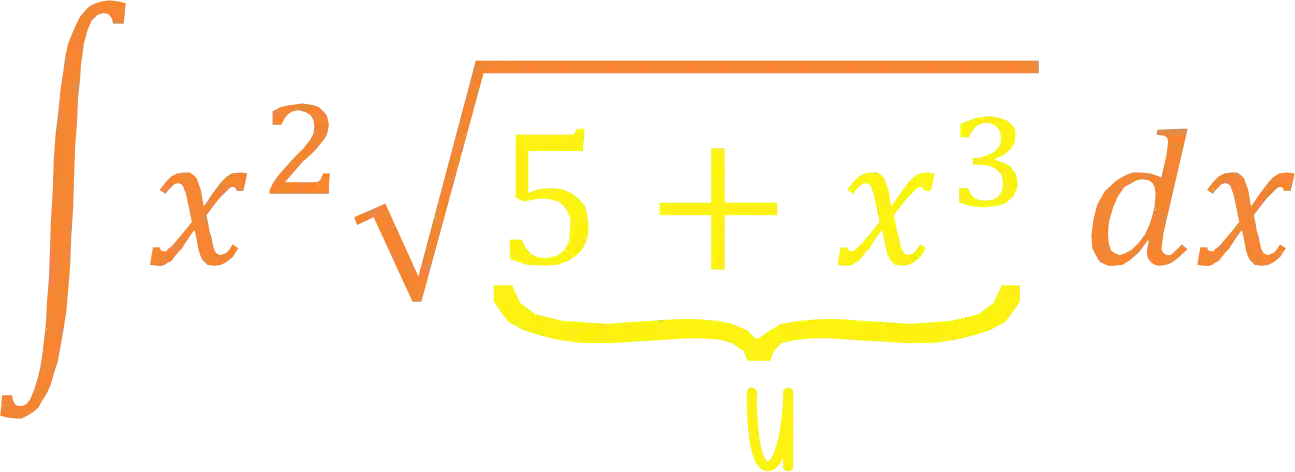
-Opa, mas como eu escolho quem vai ser o
O segredo aqui é identificar dentro da integral duas partes diferentes, onde uma deve se relacionar com a outra a partir de uma derivada. No nosso exemplo podemos dividir a integral nesses dois termos:
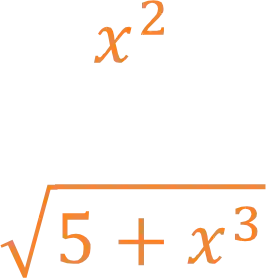
Dentro da raiz, temos a expressão,
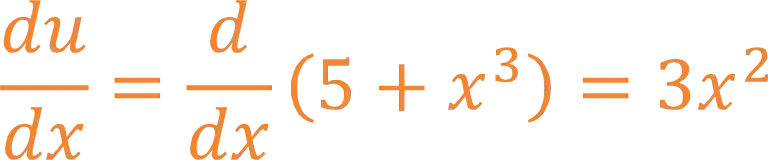
Reparou como o primeiro termo,
Passo 2: Definir
Nessa parte a gente precisa calcular a derivada de
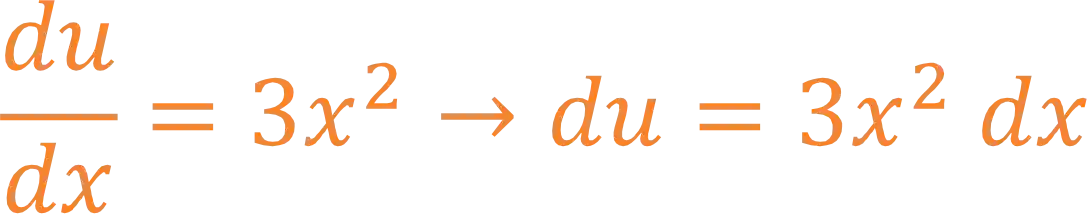
Passo 3: Substituir
Lembrando que a nossa integral é:
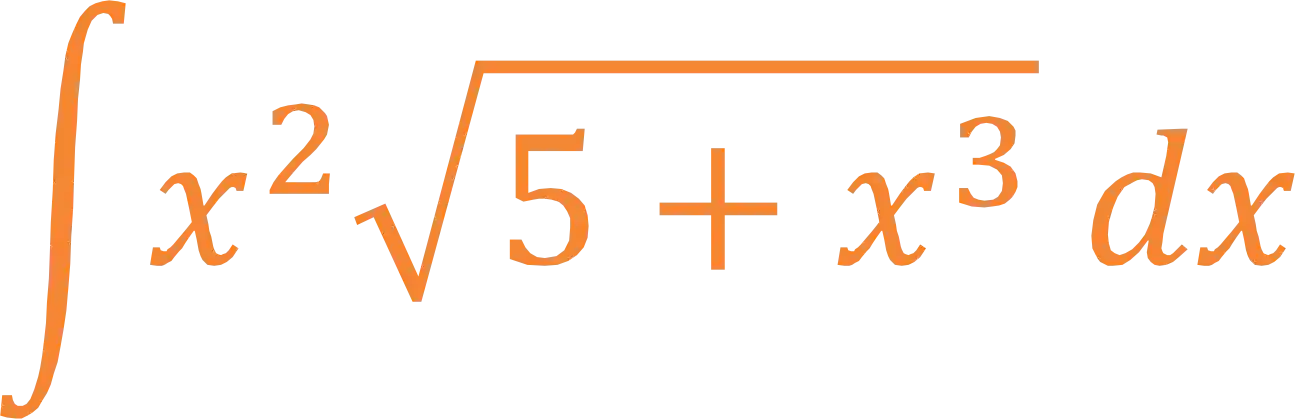
A gente já sabe quem é o
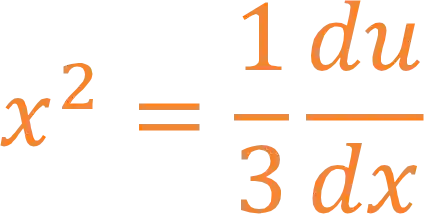
Opa! Agora sim, podemos substituir na nossa integral:
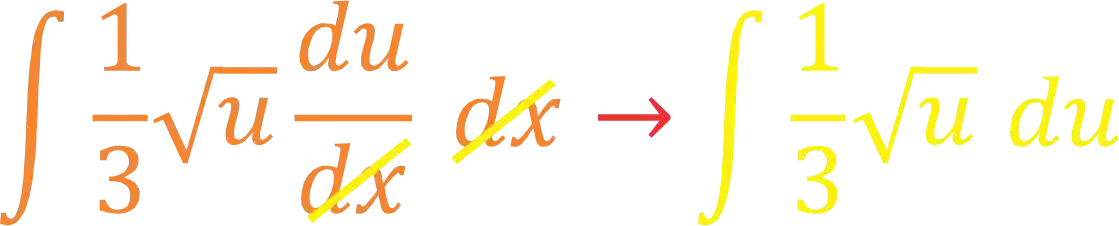
Opa, a gente já tá de cara pro gol! Que tal continuar acompanhando essa resolução no vídeo abaixo!? 👇
Passo 4: Verificar se não sobrou nenhum
No nosso exemplo encontramos, após a substituição simples, a integral:
Passo 5: Resolver a integral em relação a
Passo 6: Retornar para a variável inicial
Escrevemos que
Dicas para Escolher o
Muitas vezes, você tem que investigar, analisar e reescrever algebricamente sua integral para encontrar como dividi-la em diferentes termos para aplicar a substituição. Existem várias possibilidades para o método da substituição simples, ou seja, o que você vai escolher para substituir como
- Argumento de uma função trigonométrica
- A própria função trigonométrica
- Função exponencial ou o argumento dela
- Função logarítmica ou o argumento dela
Entre outras opções.... O importante é perceber a relação entre um dos termos que você separou e a derivada do outro termo. Vamos olhar mais um exemplo de integral:
Nesse aqui a gente pode perceber que
Substituindo na nossa integra:
E agora sabemos calcular! Só não esquece de voltar para a variável
Nesse caso o que vamos querer substituir será:
Porque quando derivarmos
E reescreveremos a integral após a substituição na forma:
E mais uma vez, depois de calcular não esquece de voltar para a variável inicial! Nesse caso teríamos:
Agora vamos praticar com exercícios?