Assíntotas
Teoria
O que é uma assíntota?
Fala aí, vamos conversar um pouquinho sobre assíntotas. E esse assunto pode ficar mais claro quando olhamos para o gráfico de algumas funções.
Dá só uma olhadinha aqui no gráfico da função
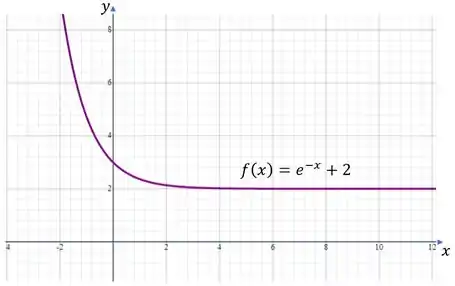
O que será que acontece se a gente colocar um valor de muuuuito grande?
Pelo gráfico parece que a nossa função vai ficando cada vez mais perto da reta , né?
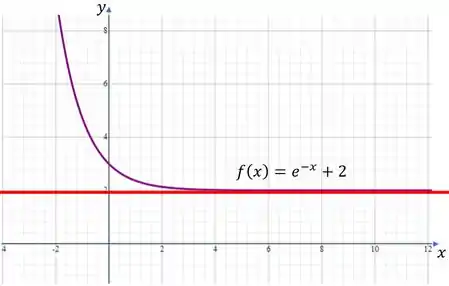
Na realidade, o que acontece é que a nossa função fica muito perto do , mas nunca chega a encostar nessa reta. Quando isso acontece dizemos que a reta é uma assíntota de , porque a função chega pertinho do dela, mas nunca encosta ou a atravessa.
Ou seja, podemos dizer que uma assíntota horizontal ou vertical nada mais é do que uma reta imaginária que delimita a aproximação de uma função no gráfico à medida que ele cresce ou decresce.
Assíntotas Horizontais
No exemplo aí de cima a gente chegou à conclusão de que a reta era um assíntota, mas ele é uma reta horizontal correto? Então, ela será uma assíntota horizontal.
Olhando o gráfico fica fácil de ver se a função se aproxima de algum valor, mas nem sempre teremos o gráfico pra ver. Então como poderemos descobrir se a função possui alguma assíntota horizontal?

Fica tranquilo que vamos achar um jeitinho.
Você percebeu que para achar nossa assíntota a gente pensou em pegar um muuuuito grande? Para representar esse muuuuuuito grande podemos usar o limite da função quando tende ao infinito. Assim:
Resolvendo esse limite encontramos:
Maneiro! Chegamos que o nosso limite é igual a 2 e essa é justamente nossa assíntota horizontal.
Beleza, mas esse não é o único caso. Veja essa outra função:
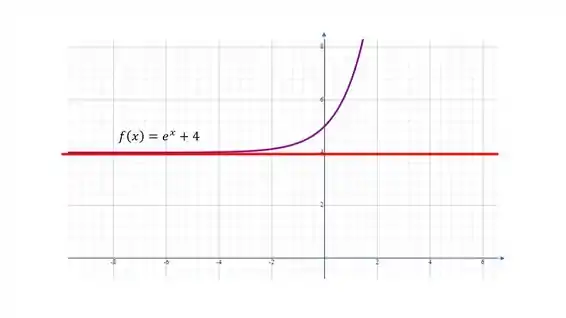
Essa reta vermelha em também é uma assíntota horizontal, mas ela acontece quando vai para menos infinito.
Então, quando a gente não tem o gráfico e queremos encontrar as assíntotas de uma função, nós pegamos um muuuuito grande nas duas direções, ou seja, tendendo ao infinito positivo e negativo.
Então, quer dizer que para acharmos uma assíntota horizontal basta a gente resolver dois limites, quando :
Onde e que será o valor da assíntota.
E quando :
Onde .
Se um ou os dois limites resultarem em um valor finito, ou seja, não explodirem pra mais ou menos infinito, quer dizer que encontramos uma assíntota horizontal.
Só fica atento que não é necessário que os dois limites sejam iguais a uma constante para ser uma assíntota, mas apenas um deles. Caso os dois limites resultem em constantes diferentes, teremos duas assíntotas, uma em cada constante.
Assíntotas Verticais
A ideia das assíntotas verticais é super parecida com a das horizontais, olha só o seguinte gráfico da função :
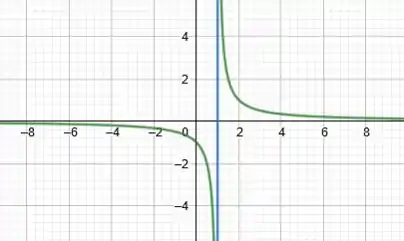
Se a gente olhar com calma quando temos um muuuito grande (tanto positivo quanto negativo) parece que a nossa função praticamente encosta na reta .
Então dizemos que essa reta é uma assíntota vertical.
Mas parece que de novo a gente resolveu só olhando pro gráfico, como faz pra resolver se não tivermos ele?
Para isso vamos procurar o valor de que faz a nossa função ir para mais ou menos infinito. No nosso caso temos um denominador que quando vai a zero, faz nossa função explodir.
Assim, procuramos qual o valor que faz isso acontecer. Como a função é . Assim o denominador vai a zero quando tende a pela esquerda ou pela direita. Então fazemos:
Então, para achar as assíntotas verticais, vamos basicamente procurar valores de que podem dar problema no nosso domínio. Devemos ficar ligados principalmente em casos em que o denominador resulta em 0 ou quando dentro de um logaritmo a expressão assume valor zero.
Sendo assim, depois de achar esses valores que dão problema na função, a gente resolve o limite com tendendo pra eles tanto pela direita quanto pela esquerda:
Se um desses dois limites explodirem para mais ou para menos infinito, ou seja, se o limite tendendo a pela esquerda ou o limite tendendo a pela direita resultarem em ou , é só partir para o abraço, porque você terá encontrado uma assíntota vertical naquele sentido 😉.
Passo a passo
Para a gente achar possíveis assíntotas horizontais nós temos que:
- Fazer os limites da nossa função com tendendo a mais e menos infinito;
- Se pelo menos um desses limites resultar em uma constante , onde . Teremos que a reta é uma assíntota horizontal;
- Se os limites derem constantes diferentes, teremos duas assíntotas;
- Se os dois limites explodirem para mais ou pra menos infinito, não temos assíntotas horizontais.
Para a gente achar possíveis assíntotas verticais nós temos que:
- Achar valores de que dão problema na nossa função, ou seja, que não estão no domínio dela (lembrar dos principais casos);
- Fazer os limites laterais da função com tendendo aos valores problemáticos;
- Se um desses limites laterais explodirem para mais ou menos infinito, quer dizer que temos uma assíntota vertical;
- Se os dois limites resultarem em constantes, não temos assíntotas verticais.
Com esse passo a passo a gente acha qualquer assíntota que a função possa ter. Então, pra ficar fera, vamos partir para os exercícios!!!
Assíntotas Verticais
Passo a passo
Exercícios Resolvidos
Exercício Resolvido #1
Unicamp, Cálculo 1, 2019.2, P1, Questão 5.
Encontre as assíntotas horizontais e verticais da função .
Passo 1
Opa, tudo bom? Vamos ver quem são essas assíntotas!
Beleza pessoal, pra começar essa questão a gente tem que lembrar das definições de assíntotas horizontais e verticais.
Primeiro vamos lembrar da aparência de cada uma delas com um exemplinho:

A imagem já ajuda bastante a entender as definições:
- A assíntota horizontal acontece nesse caso aqui:
Repare que o gráfico da função quase toca na reta horinizal, mas isso nunca acontece, mas quanto maior for o nosso valor de , mais próxima dessa reta nossa função estará. Então, quando queremos descobrir qual a assíntota horizontal, o que queremos na verdade é saber qual o valor dessa reta, que é o limite da função quando .
- E a assíntota vertical acontece nesse aqui:
Agora a pergunta já será diferente, o que queremos saber é, para que valor o tende quando nossa função vai para . Esse valor de será a reta vertical, que quase encosta no gráfico da nossa função.
Passo 2
Vamos começar calculando as assíntotas horizontais, que geralmente são mais fáceis de encontrar.
É só calcular o limite quando tende a mais/menos infinito. Começamos com :
Isso é o limite da divisão de dois polinômios. O que a gente pode fazer nesses casos? Uma boa tentativa é dividir tudo pela maior potência.
Nesse caso a maior potência é , então vamos dividir por em cima e embaixo:
Agora o que acontece quando tende ao infinito?
Quando fica muito grande, aquelas duas frações vão tender a zero! Então:
E o resultado vai ser exatamente o mesmo com :
Então a função tem duas assíntotas horizontais em :
Passo 3
Agora vamos procurar as assíntotas verticais. Esse tipo de assíntota aparece quando a função “explode” para cima ou para baixo perto de algum ponto:
Como que uma função pode explodir desse jeito? Bom, ou o numerador fica muito grande, ou o denominador fica muito pequeno.
O numerador só fica muito grande quando tende ao infinito, mas a gente já viu que isso caiu numa assíntota horizontal.
Então como a gente pode fazer pro denominador ficar muito pequeno? Pra isso, é só ver qual valor de faz ele se aproximar de zero!
Passo 4
Mas pra provar mesmo que a gente tem uma assíntota nesse ponto, temos que calcular o limite de tendendo a ele:
E para esse limite a gente vai ter que analisar os limites laterais, ou seja e
Quando o se aproxima do pela esquerda, ele se comporta mais ou menos assim:
Ou seja, ele sempre fica abaixo do , e por isso fica sempre negativo. Por isso, quando a função explode, ela explode pra baixo.
Quando o se aproxima do pela direita, ele se comporta mais ou menos assim:
Então ele sempre fica acima do , e o vai ficar sempre positivo, e aí a função vai explodir pra cima:
Assim, provamos que a função tem duas assíntotas verticais em .
Passo 5
Pra garantir que não vai sobrar dúvida, vamos fazer o gráfico da função, mostrando as assíntotas verticais em e as horizontais em :

Resposta
A função tem assíntotas horizontais em , e assíntotas verticais em .
Exercício Resolvido #2
UFF, Cálculo IA-Lista 4, GMA, 2008-1, Questão 12
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Passo 1
Opaa! Vamos continuar com nossos exercícios de assíntotas!
Lembrando que a gente acha as assíntotas fazendo isso aqui
- A assíntota horizontal acontece nesse caso aqui:
- A assíntota vertical acontece nesse aqui:
A pergunta é: Pra que valor a função vai quando tende a ?
E a pergunta é: tende pra que valor quando a função vai pra ?
Passo 2
As assíntotas verticais são aquelas que ocorrem perto de pontos “problemáticos” da função. Esses pontos problemáticos são justamente os pontos de descontinuidade, que podem ser denominadores dando zero, raiz negativa, ...
No caso da função dada,
A única restrição que temos que analisar é quando o denominador da fração é zero. Isso ocorre quando:
Então, como queremos achar as assíntotas verticais da função, precisaremos ver os limites laterais quando tende a , ou seja, e
Quando o se aproxima do pela esquerda, ele se comporta mais ou menos assim:
Ou seja, ele sempre fica cada vez mais próximo, porém sempre abaixo do , e por isso fica sempre negativo. Por isso, quando a função explode, ela explode pra baixo.
Quando o se aproxima do pela direita, ele se comporta mais ou menos assim:
Então ele sempre fica cada vez mais próximo, porém sempre acima do , e o vai ficar sempre positivo, e aí a função vai explodir pra cima:
Portanto, é assíntota vertical tanto pela esquerda quanto pela direita.
Passo 3
Agora vamos ver as assíntotas horizontais, aquelas que ocorrem com tendendo a .
Primeiro para
Vamos apenas resolver esse limite dividindo em cima e embaixo por
Show, agora vamos fazer o limite de
Portanto, há uma assíntota horizontal em .
Resposta
Verticais:
Horizontais:
Exercício Resolvido #3
UNICAMP - Cálculo 1 - P1 2015 Noturno – 3
Encontre as assíntotas verticais e horizontais da seguinte função
Passo 1
Opaa, fala aí! Vamo que vamo fazer mais uma questão de assíntotas!
Antes de qualquer coisa, vamos analisar o numerador e denominador de e tentar abrir em um produto de polinômios irredutíveis. Isso vai facilitar os cálculos mais a frente, então vamos simplificar um pouco.
Começando com o numerador:
Podemos colocar em evidencia, assim:
Agora para o denominador, vamos fazer Baskhara
Sendo , e
Isso fica
Que nos dá duas raízes
Com as raízes em mãos, podemos reescrever nosso polinômio usando
Então nosso denominador se transforma em:
Com isso, podemos reescrever , dessa forma:
Então, simplificando, temos:
Bem mais de boinhas, né??
Maaas, mesmo cortando o em cima e embaixo, está fora do domínio, por zerar o denominador original.
Ok, vamos procurar as assíntotas agora.
Passo 2
Seguinte, Assíntotas verticais aparecem onde o domínio não está definido e as horizontais aparecem quando calculamos o limite de .
Começando com as verticais, o domínio não está definido em
Quando o se aproxima do pela esquerda, ele se comporta mais ou menos assim:
Ou seja, ele sempre fica abaixo do , e por isso fica sempre negativo. Por isso, quando a função explode, ela explode pra baixo.
Quando o se aproxima do pela direita, ele se comporta mais ou menos assim:
Então ele sempre fica acima do , e o vai ficar sempre positivo, e aí a função vai explodir pra cima:
Assíntota vertical em .
Mas você deve tá se perguntando “e que raios aconteceu com o que também ta fora do domínio??”
É normal ficar nessa dúvida, então vou te mostrar o que aconteceu com o a gente viu que também não está no domínio da função original, já que aparece um no denominador de . Porém, o que acontece é que, ao calcularmos seu limite quando veremos que ele converge para um valor, e não para , não consistindo em uma assíntota vertical!
Passo 3
Agora para as assíntotas horizontais
Vamos usar o limite de em e em
Achamos uma mesma assíntota horizontal, .
Resposta
Exercício Resolvido #4
Esboço de Curvas
Considerando a função
Determine todas as assíntotas verticais e horizontais ao seu gráfico.
Passo 1
E aiii! Vamos continuar com nossos exercícios para ficar fera em assíntotas!
Para descobrir as assíntotas verticais devemos pensar em descontinuidades no domínio. Já para as assíntotas horizontais devemos procurar os limites de com .
Passo 2
Começando com as assíntotas verticais, notamos que o domínio não está definido em , valor que zeraria o denominador de .
Vamos ver então os limites laterais quando se aproxima de pra ver o que acontece!
Quando o se aproxima do pela esquerda, ele se comporta mais ou menos assim:
Ou seja, ele sempre fica abaixo do , e por isso fica sempre negativo. Por isso, quando a função explode, ela explode pra baixo.
Quando o se aproxima do pela direita, ele se comporta mais ou menos assim:
Então a gente tem
Como qualquer número elevado ao quadrado é positivo, ficamos com
Assim, vemos que para nossa função explode para . Então o é uma assíntota vertical.
Passo 3
Vamos pensar agora nas assíntotas horizontais usando o limite para em e em :
Achamos a mesma assíntota nos dois limites, .
Resposta
Exercício Resolvido #5
Calcule as assíntotas horizontais e verticais da função
Passo 1
Opa, tudo certinho? Espero que sim! Vamos seguir com nossos estudos!
Bora lá começar então pelas assíntotas horizontais. Pra encontra-las, basta fazer os limites:
Pra que a assíntota exista, o limite deverá ser igual à um valor finito e esse valor será nossa assíntota.
Para calcular esses limites, podemos organizar melhor a função fatorando no numerador e o denominador:
Pra isso, vamos colocar em evidencia em cima e embaixo:
Assim, podemos cortando os , e teremos:
Agora podemos aplicar o limite de
Substituindo nas frações, teremos . Assim:
Perfeito! Chegamos à conclusão então que é uma assíntota vertical
Passo 2
Agora pra fechar a questão a gente parte para as assíntotas verticais.
Aqui vamos fazer os limites laterais e descobrir para que valores teremos o limite da função indo para .
Mas para achar quais valores de vamos usar, olha bem a função:
Como ela é uma fração, podemos desconfiar que o limite irá para quando o denominador for para zero.
Então vamos fazer os limites laterais exatamente pros pontos que zeram o denominador de , isto é, .
Então e são possíveis pontos de assíntotas verticais!
Passo 3
Vamos testar. Para
Show, deu infinito, então é assíntota vertical!!
Passo 4
E pra :
Show, também deu infinito, então também é uma assíntota vertical.
Assim encontramos todas as nossas assíntotas.
Resposta
Assíntota horizontal
Assíntotas verticais e
Exercício Resolvido #6
UFF, Cálculo IA-Lista 4, GMA, 2008-1, Questão 14
Determine as equações das assíntotas verticais e horizontais do gráfico da função dada.
Passo 1
Oiii, estamos seguindo com as nossas questões de assíntotas, cada vez um passo mais próximo de ficar fera nesse assunto.
As assíntotas verticais são aquelas que ocorrem perto dos pontos de descontinuidade. No caso da função dada, isso ocorre quando o denominador é nulo, pois isso fará com que a função exploda para .
Lembrando que a assíntota vertical é algo tipo assim
Então, acharemos o valor da assíntota descobrindo a qual valor o se aproxima quando o denominador é igual a zero:
Para resolver essa equação, podemos colocar em evidência:
Temos aqui um produto dando zero. Opa, nesse caso a gente tem dois pontos onde esse denominador zera! São eles?
Podemos ter assíntotas verticais em e . Vamos verificar.
Passo 2
Vamos começar verificando o analisando os limites laterais e e vendo se esse limite realmente explode indo para , nesse valor:
Para tentar dar um jeito, vamos dividir em cima e embaixo por e simplificar:
Quando a gente tem um número dividido por zero pela esquerda ele fica negativo e tende a menos infinito, então temos:
Agora para
Show! Deu portanto, é assíntota vertical.
Passo 3
Agora vamos verificar o pela esquerda e pela direita.
O limite também deu então também é assíntota vertical.
Passo 4
Certo, agora vamos procurar as assíntotas horizontais.
A assíntota horizontal acontece nesse caso aqui:
Então vamos lá, começando por
Simplificamos dividindo tudo por
E aplicando o limite:
Show, achamos um valor finito! Vamos ver agora para
Achamos novamente um valor finito. Portanto, há uma assíntota horizontal em .
Resposta
Verticais:
Horizontais:
Exercício Resolvido #7
Esboço de Curvas
Determine todas as assíntotas ao gráfico de
Passo 1
Fala aiiii! Esse exercício aí parece mais sinistro, mas fica tranquilo que vai ficar de boinhas com essa explicação aqui
Procuramos as assíntotas da seguinte maneira: as assíntotas horizontais se relacionam com o limite de quando e as assíntotas verticais se relacionam com as descontinuidades quando são pontos fora do domínio de que levam a função para .
Como nossa função é uma fração, o domínio de é representando por todos os números reais, menos aqueles que zeram o denominador. Para encontrar os valores de que estão fora do domínio faremos:
Logo, . Isso indica que o zero é uma possível assíntota.
Passo 2
Para saber se o zero realmente é uma assíntota, vamos analisar os limites laterais da função e , e ver se isso fará com que a função vá pra .
Aplicando os limites laterais:
Logo, é assíntota vertical!
Passo 3
Agora vamos ver as horizontais!
Nesse caso, vamos fazer o limite . Se o limite existir e for para um valor finito, esse valor será nossa assíntota.
Se substituirmos, temos
Xiii, deu uma indeterminação!
Então, vamos ter que dar uma mexidinha ai!Uma boa forma de nos livramos do problema da indeterminação é somar e diminuir do numerador, e aí a gente fica com isso aqui:
Que a gente pode separar em duas frações
Na primeira fração, podemos cortar dos dois lados, ficando com
Aqui vamos aplicar o limite novamente e ver se isso resolveu o problema
Substituindo por temos
Como , temos:
Oba! Deu certo. E como é um valor finito, o será uma assíntota horizontal!
Agora para
Quando temos , que tende a zero!! Então podemos substituir direto na equação, ficando com:
Também deu certo. E temos outra assíntota horizontal.
Assim, são duas assíntotas horizontais, e
Resposta
Exercício Resolvido #8
CEFET - Cálculo 1 - P1 Romulo 2014.2 – 4
Encontre as assíntotas horizontais e verticais para:
Passo 1
Fala aiii! Bora continuar estudando pra ficar fera nessa matéria!
Opa, mas o que é isso? tem um aí no meio, o que a gente faz agora?
A primeira coisa a fazer é organizar essa função escrevendo :
E para isso, começaremos separando o que tem para um lado e o que não tem pro outro:
Agora vamos colocar em evidência!
Dividindo os dois lado por , temos:
Pronto, agora sim, temos uma função escrita de maneira mais familiar.
E como ela é uma fração, é bom analisar logo o seu domínio.
Seu denominador não pode zerar, como o que acontece em e em . Com isso seu domínio será, portanto:
Passo 2
Para ver quem são as assíntotas horizontais faremos o limite para na função:
Aplicando diretamente o limite, cairemos em uma indeterminação do tipo .
O jeito é colocar em evidência
Cortando esses safadinhos, ficamos com:
Show, agora a gente pode substituir, lembrando que
Como o limite nos deu um valor finito ele será nossa assíntota horizontal.
Agora para , vamos fazer algo bem parecido
Pelos resultados temos duas assíntotas horizontais sendo .
Passo 3
Para assíntotas verticais temos que olhar para onde o domínio da função não está definido (nesse caso, em como vimos lá atrás) e lançar os limites laterais ali:
Começando com
Pelo lado direito, temos um valor de indo para , porém um pouquinho maior que 1, o que fará com que o denominador seja positivo:
Assim teremos:
Agora pelo lado esquerdo, termos um valor de indo para , mas agora um pouquinho menor que , o que fará com que o denominador seja negativo:
Com isso, vemos que é uma assíntota vertical.
Agora para (atenção que com o sinal trocado, temos uma pegadinha aqui, se liga)
Então, para . Pelo lado direito:
E pelo lado esquerdo:
Feito isso, sabemos que temos assíntotas verticais em e
Resposta
Exercício Resolvido #9
PUC-RJ - Cálculo B - P2 2014.2 - 3 a b
Seja . Determine o que se pede, justificando adequadamente o que não há.
Domínio de .
Assíntotas horizontais e verticais da curva
Passo 1
Opa, e aí! Vamos continuar que estamos na reta final, seu esforço vai gerar resultado 😊!
Para o domínio de devemos lembrar que o termo dentro de um logaritmo deve sempre ser enquanto o termo dentro de uma raiz quadrada deve sempre ser . No fim das contas, o objetivo é ter:
Pera, mas não existe log de número negativo, certo? Bom, isso significa que nosso domínio será todo o espaço real. Isso faz sentido uma vez que e são dois valores sempre positivos e, portanto, sua soma também é.
Já fica a dica aqui, como a gente não tem descontinuidade, não podemos ter assíntotas verticais (se não a gente ia colocar tendendo a quê né? Hehe)
Passo 2
Uma vez que não existem descontinuidades no domínio não vamos ter assíntotas verticais. Sendo assim, vamos focar em assíntotas horizontais usando o limite em
Puts, a assíntota horizontal ter que dar um resultado finito, então não temos assíntota horizontal aqui!
Vamos ver para
Quando temos ele tende a zero! Então ficamos com
Logo, temos uma assíntota horizontal em
Resposta
Exercício Resolvido #10
Questão 3: Seja dada por
Encontre a assíntota horizontal de quando . E diga se existe assíntota vertical em algum ponto?
Passo 1
Oiii! Vamos continuar nossos estudos pra aprender tudinho!
Bem, o problema já indicou que existe assíntota horizontal. O seu método de calcular é justamente aplicando um limite para tendendo ao infinito. No caso temos que avaliar nos dois infinitos, um positivo e o outro negativo...
Passo 2
Vamos começar pelo infinito positivo
Como estamos no lado positivo e indo para o infinito (então maior que ) usamos a primeira expressão de ...
Dividindo em cima e em baixo por ...
Quando cresce muuuuuito, essas frações vão a ...
Então, já encontramos uma assíntota horizontal:
Passo 3
Vamos averiguar agora para o lado do infinito negativo.
Como estamos no lado negativo e diminuindo cada vez mais, a função é a segunda expressão...
Como o limite foi para não tem assíntota desse lado, e a única horizontal é a mesmo.
Passo 4
A segunda pergunta desse item, foi se existe uma assíntota vertical em algum ponto, e a melhor resposta por hora é: pode existir. Afinal essa assíntota ela depende de algum ponto de que possivelmente tenha problema.
Se você observar a função novamente...
Repare que o único ponto de que pode dar problema é em , pois aí a função tem uma divisão por .
Então é uma provável assíntota vertical. Vamos averiguar!
Passo 5
Vamos ver os limites laterais!!
Primeiro pela direita dele
Repare que o numerador está tendendo a um número, e o denominador a pelos positivos, como tem um sinal de na frente, a função está tendendo ao infinito negativo...
Então nem precisa averiguar o outro lado não, é uma assíntota vertical ;)
Resposta
Assíntota horizontal:
E existe uma assíntota na vertical em .