Indeterminação com x constante
Teoria
Fala aí. Você se lembra de qual é a primeira coisa que nós fazemos quando temos um limite pra resolver? Tipo esse limite aqui:
Bem, a primeira coisa é tentar substituir o pelo valor de sua tendência na função. Vamos tirar o operador e colocar o em todos lugares que tiver . Assim:
E prontinho, limite calculado tranquilamente.
Agora que a gente relembrou o primeiro passo, vamos fazer esse outro limite aqui:
Vamos a substituição:
Opaaaa! Quanto é ? 0? 1? E agora José?
Bom, esse valor não está matematicamente definido, é uma indeterminação matemática. Existem vários tipos de indeterminações, onde as mais comuns são:

Fique calmo(a) que hoje estamos recheados de coisas novas. Mas acredite, dará tudo certo no final. Vem comigo!
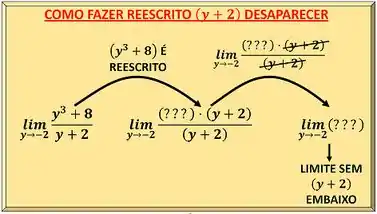
Quando isso acontece, nós não conseguimos calcular o limite da função apenas substituindo os valores da tendência do . Mas isso não significa que o limite não existe, apenas teremos que arrumar outra forma de calcular ele. Mas relaxa porque vamos te mostrar o caminho das pedras!
E agora? Como calcular esse limite?
Você concorda que nosso grande problema é que o zera tanto o numerador quanto o denominador?
Então, a ideia aqui é arrumar uma forma de reescrever essa função de maneira que isso deixe de acontecer e faremos isso usando a fatoração, que nada mais é do que uma forma de reescrever uma expressão matemática. Vamos então entender como podemos fatorar cada parte dessa função:
- O numerador :
- O denominador :
- Fator comum:
Ele é um polinômio de dois termos, o e o . Como nos dois termos temos o aparecendo, podemos tirar ele de cada termo colocando evidência na frente, abrimos os parênteses e colocamos o que sobrou depois de retirar esse .
Assim:
Pra você conferir se está mesmo fazendo a coisa certa, basta multiplicar o que você colocou em evidência, ao fazer isso, você precisa encontrar o que tinha antes. Assim você saberá se fatorou de maneira correta.
Aqui também temos dois termos, mas não há fator comum entre eles. Mas, podemos desconfiar de outro tipo de fatoração, a diferença de quadrados. E pra fazer os quadrados aparecerem, vamos escrever o como sendo o .
A diferença de quadrados é um produto notável que tem essa carinha:
Tendo uma expressão que se encaixa em um dos dois lados da igualdade, podemos reescrever a expressão com o que temos do outro!
No nosso caso, colocando o no lugar do e o no lugar do , teremos:
Ótimo! Tudo bem fatoradinho! Então vamos reescrever nosso limite e ver o que pode ser feito.
E olha que coisa boa, temos em cima e embaixo, então podemos cortar os dois pois eles estão numa multiplicação. Assim:
Agora ficou mais agradável! Depois de fazer esse processo a gente tenta substituir o limite novamente e vê se é possível calculá-lo:
E olha, deu um valor existente. Assim, conseguimos calcular o limite e ele é igual a .
Situações desse tipo são bem comuns no estudo de cálculo. Então, qual a ideia fundamental?
Você tenta substituir o valor do , se for possível calcular o limites, MARAVILHA! Mas caso você caia em uma indeterminação, o jeito é reescrever a função fatorando e reorganizando tudo para que seja possível fazer o limite.
Mas parece que eu tirei vários coelhos da cartola na hora de fatorar, não foi?

Na verdade, de acordo com tipo de função que nós encontramos, poderemos desconfiar de algum tipo específico de fatoração. Vamos dar uma olhada melhor nisso.
Fatoração de polinômios
Tá, mas como saber qual o tipo de fatoração a gente deve usar?
Existem várias fatorações diferentes, e a função lhe dará algumas pistas. Vamos ver quais são elas:
É sempre a primeira coisa que vamos procurar. Se percebemos que há um fator que é comum em todos os termos, poderemos colocar ele em evidência. Veja alguns exemplos:
O 3 é comum aos dois termos, colocamos ele em evidência da seguinte forma:
Repara que quando a gente tira todo o fator do termo, sempre precisará sobrar o pra completar aquele lugar.
Veja outro caso:
Vemos que os dois termos tem o , mas além disso, os dois possuem números que são múltiplos de , assim, podemos colocar tanto o , quanto o em evidência:
Esses são alguns casos bem comuns, vamos ver outras situações.
- Diferença de quadrados:
- Polinômios do 2º grau:
- Produtos notáveis:
- Numerador:
- Denominador:
Quando o polinômio for uma diferença de dois valores elevados ao quadrado, a fatoração será a soma das raízes multiplicada pela diferença dessas mesmas raízes, assim com fizemos no exemplo ali em cima!
Veja:
Quando nos depararmos com um polinômio do 2º grau, que não se encaixe em outro esquema de fatoração, podemos fatorar ele usando a fórmula de Bháskara. Por exemplo:
Primeiro, vamos identificar quem são os coeficientes correspondentes na nossa fórmula geral:
A ideia então é aplicar a fórmula de Bháskara e descobrir as raízes e pra reescrever o polinômio no limite na sua forma fatorada:
Não esquece desse aí quando ele for diferente de !
A fórmula de Bháskara é essa:
Substituindo os coeficientes da nossa expressão, temos:
Vamos separar esse aí, ficando com
Assim, e , escrevendo a forma fatorada:
Prontinho, fatorado!
Os produtos notáveis são expressões comuns de aparecerem por aí e que tem resultados já conhecidos, por isso facilitam a nossa vida na hora de fatorar.
Os principais produtos notáveis são:
Caso você precise fatorar um polinômio que se encaixa em alguma dessas expressões, você pode aplicar diretamente a fórmula e reescrevê-lo!
Vamos pensar em um exemplo para calcular o limite:
Aplicando diretamente o limite teremos:
Opa! Indeterminação!!!
Então, partiu fatorar esses polinômios aí pra melhorar isso.
É uma diferença de quadrados do tipo , que fatorada fica:
É um polinômio do 2º grau que não se encaixa em nenhum produto notável. Então, vamos usar a Bháskara!
Fazendo , e
Vamos separar esse aí, ficando com
Assim, e , escrevendo a forma fatorada:
Prontinho, fatorado!
Agora, vamos organizar o que achamos no limite:
Olha que maravilha, podemos cortar o de cima com o de baixo, ficando com:
Agora nós tentamos aplicar o limite novamente, substituindo o por :
Prontinho, limite devidamente calculado, sem problemas de indeterminação!
É essa a ideia, você usa um produto notável para manipular o limite e sair das indeterminações.
Limites com raiz quadrada:
Agora chegou a hora de calcularmos esse limite aqui:
Aplicando diretamente o limite, teremos:
Opa! Já sabe né! Indeterminação.
Aqui, podemos usar uma forma bem comum para casos de indeterminação com raízes. Vamos multiplicar nossa função em cima e embaixo pelo conjugado da parte que está com a raiz.
Mas o que é o conjugado?
Ele é a expressão com operação contrária a que está sendo feita com a raiz.
No nosso caso, o está sendo subtraído da raiz, então o conjugado será o sendo somado a ela:
Então, multiplicamos por ele em cima e embaixo:
Repare que na parte de baixo temos uma multiplicação do tipo soma vezes diferença, que lembra a fatoração da diferença de quadrados que vimos lá atrás:
O que precisamos é fazer o caminho inverso. Assim:
Lembrando que elevar ao quadrado e fazer a raiz quadrada são operações que se anulam, por isso sobra só o :
Reescrevendo a parte de baixo da função nesse formato, teremos:
E poderemos cortar o de cima como de baixo, ficando apenas com:
Agora aplicamos diretamente o limite:
E mais uma vez, limite devidamente calculado!
Essa história de multiplicar pelo conjugado, nós podemos usar sempre que precisarmos eliminar a raiz em um limite.
E depois de ver tudo isso, só mesmo fazendo bastante exercício pra treinar. Então, vamos a eles!
Fatoração de polinômios
Limites com raiz quadrada:
Exercícios Resolvidos
Exercício Resolvido #1
Resolva o limite:
Passo 1
E aí! Pronto para mais uma etapa nessa nossa missão de entender tudo de limites?
Primeiro, vamos lembrar do primeiro passo que sempre precisamos seguir para resolver qualquer questão de limite!

Relaxa, porque é normal não lembrar de tudo no início!
O primeiro passo é substituir pelo valor para onde está indo, que é esse indicado aí embaixo do . Nessa questão, está caminhando em direção a . Logo, precisamos substituir o por em toda a expressão e calcular, pra ver no que vai dar.
O resultado deu (zero dividido por zero). No entanto, não é possível calcular quanto vale zero dividido por zero . Não dá pra dividir um número por zero! Por exemplo, podemos dividir balas por 2 pessoas (cada pessoa fica com 5 balas). Podemos dividir 10 balas por 1 pessoa (a pessoa fica com as 10 balas). Mas como vamos dividir 10 balas por 0 pessoas?

Como vemos pela figura acima, é impossível dividir por 0! Não temos pessoa para fazer essa divisão! Então nunca podemos ter um na parte de baixo de uma fração (denominado). Por isso, o resultado dessa divisão fica indeterminado, e chamamos a divisão de indeterminação. Ou seja, não podemos responder a questão com !
Passo 2
O primeiro passo mostrou que ainda não podemos substituir por , porque isso faz a parte de baixo da fração valer zero . Ou seja, isso gera uma indeterminação ! Logo, antes de substituir por , temos que nos livrar do presente na parte de baixo da fração!

Para o desaparecer da parte de baixo da fração, temos que fazer aparecer na parte de cima da equação! Assim, vamos poder cortar o de baixo com o de cima!
Para isso, vou te lembrar de um negócio chamado produto notável! Mais especificamente da diferenção de dois números elevados ao quadrado. Ela é muito legal, pois pode ser escrita como:
Assim estamos trocando dois números elevados ao quadrado ( e ) por somas e subtrações mais simples e . Usar esse produto notável pode funcionar para o nosso caso, porque um dos nossos termos do nosso limite, que é o , se parece muito com o termo do produto notável.
A primeira vista você pode não concordar com isso, porque em existem dois números elevados ao quadrado ( e ) e em apenas o está elevado ao quadrado. No entanto, se a gente se lembrar que , a semelhança vai ficar mais clara.
Com essa sacada conseguimos perceber quanto valem e para o nosso caso.
Usando esse produto notável, a gente consegue reescrever e de quebra fazer o termo aparecer na parte de cima da fração!
Agora vamos reescrever o limite e ver o que sai.
Passo 3
Reescrevendo, ficamos com isso aqui:
Vou cortar o , ok?
O que vai transformar nosso limite em :
Substituindo novamente por :
O que não nos gerou nenhum tipo de indeterminação, então:
Uhuuulll! Resultado em mãos, acabou a questão.
Resposta
Exercício Resolvido #2
Calcule o limite, se existir.
Passo 1
Podemos pensar em calcular esse limite apenas substituindo o valor na expressão, entretando, ao fazer isso, ficamos com a inderterminação , observa.
Aí não dá pra trabalhar, né? Então fazemos o que? Vamos então fazer manipulações para tirar essa indeterminação, só analisar um pouco e vamos descobrir, calma que vai da certo!
Passo 2
Vamos tentar manipular o numerador, resolvendo a expressão elevada ao quadrado:
Um número ao quadrado é como se fosse ele vezes ele mesmo, certo? Então vamos fazer isso
Pra resolver essa multiplicação precisamos lembrar da multiplicação de polinômios
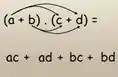
Nesse caso, nosso
Agora podemos colocar o em evidência e simplificar com o do denominador, vamos lá:
Passo 3
Pronto, agora é simples, só substituir o valor na expressão:
Resposta
Exercício Resolvido #3
Calcule o limite, se existir.
Passo 1
Para calcular o limite o primeiro passo sempre é tentar substituir o valor do pelo valor que ele está tendendo. No caso o , isso porque temos escrito embaixo do . Vamos tentar?
Cacara, que bad, ficamos com a inderterminação .
É preciso então fazer alguma manipulações para tirar essa indeterminação, vamos analisar um pouco e descobrir. Calma que vai da certo!
Passo 2
Vamos lá, vamos analisar o limite:
Olhando cuidadosamente vemos que o que está atrapalhando a gente é esse aí do denominador. Vamor ter que dar um jeito de tirar ele dali.
Pra isso, podemos fatorar a expressão do numerador na intenção de aparecer alguma coisa que ajude a gente, e um dos métodos é usando a fórmula de Bhaskara. Vamos lá?
Pegando
Temos o formato:
Como:
Para descobrir qual o valor de , vamos usar a fórmula:
Onde
Substituindo obtemos:
Agora aplicando na fórmula do , temos:
Assim, as raízes são:
e
A intenção aqui é reescrever a equação com essas raízes, transformando ela em logo
Olha quem apareceu ali. Logo o que a gente estava precisando.
Estamos fazendo isso para podermos reescrever o nosso limite lá do começo de uma maneira que não nos dê uma indeterminação.
Reescrevendo, teremos:
Agora sim, bem mais simples!
Passo 3
Agora vamos analisar o limite que simplificamos:
Podemos ver que a expressão aparece tanto no numerador quanto no denominador, Assim podemos cortar o de cima com o de baixo e nossos problemas estarão resolvidos.
Vamos então aplicar novamente o limite com Que é só substituir o valor na expressão, simples assim:
Chegamos a nossa resposta.
Resposta
Exercício Resolvido #4
Calcule o limite abaixo usando as propriedades operatórias:
Passo 1
Faaala! Como estão os estudos? Decolando?!
Se liga! Esse é um exercício de limite. Qual é o primeiro passo de todo exercício de limite?
Isso aí. Substituir a variável pela tendência da variável! Nesse caso, a variável é o . A tendência da variável é valer . Logo, temos que substituir por :
É, deu ruim! O resultado dessa substituição foi uma divisão de zero por zero . Xiiii, não é possível dividir um zero por zero! Essa divisão é uma indeterminação. Vamos ter que encontrar um outro método de solução!
Passo 2
Se tentarmos descobrir o que deu errado nessa substituição de por , veremos que a culpa de tudo é da parte de baixo da fração ! Como , quando , o resultado vira uma divisão por zero impossível de ser calculada! Logo, antes de substituir por , temos que nos livrar do que está embaixo da fração!
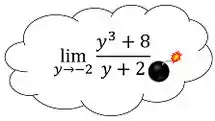
Para o desaparecer da parte de baixo da fração, temos que fazer aparecer na parte de cima ! Se fizermos isso, vamos poder cortar o debaixo com o de cima! Em outras palavras, temos que reescrever a parte de cima da equação de forma que apareça .
Fazemos isso através de um produto notável que não é muito comum, mas será bem útil para o que estamos precisando.
Isso pode funcionar para o nosso caso, porque o termo do limite se parece muito com o termo do produto notável! Olhando rápido você pode achar que os dois não se parecem, porque em existem dois números elevados ao cubo ( e ) e em apenas o está elevado ao cubo. No entanto, se a gente se lembrar que :
Usando essa informação, fica mais fácil de ver quanto e valem para o nosso caso.
Como já sabemos quem está no lugar do e do , vamos reescrever o produto notável no mesmo formato, mas agora trocando o por e o por :
Usando esse produto notável, a gente consegue reescrever e, de quebra, fazer o termo aparecer na parte de cima da fração!
Agora vamos reescrever o limite e ver se isso nos ajudor na hora de substituir por novamente.
Passo 3
Reescrevendo, ficamos com isso aqui:
Com isso podemos cortar o da parte de cima e da parte de baixo.
Ficando apenas com:
Substituindo novamente por , podemos achar o valor certo do limite sem nenhuma indeterminação para nos atrapalhar!
Parabéééns! Mais um exercício concluído! Vamos que vamos!
Resposta
Exercício Resolvido #5
Calcule o limite, se existir.
Passo 1
Ao aplicarmos o limite substituindo o por , teremos:
Opa. Temos aí uma indeterminação do tipo . O que não pode acontecer!
Teremos que tomar providências com esse aí que está nos dando problemas.
O bom é que quando temos raízes quadradas, podemos melhorar um pouquinho nossa questão multiplicando a expressão pela sua conjugada.
Bom galera, para começar vamos fazer uma boa adaptação! Basta lembrarmos que:
Observa que queremos sumir com aquela raiz ali, certo? Então vamos usar esse produto notável pra conseguir elevá-lo ao quarado. Mas tudo que multiplicamos embaixo, temos que também multiplicar em cima! Assim é como se estivéssemos multiplicando por 1, que não muda nada
Então vamos multiplicar em cima e embaixo por que é o tal conjugado de
Então:
Aplicando o produto notável na parte de baixo vamos ficar com:
Podemos agora cortar o do denominador e numerador ficando com:
Agora podemos aplicar o limite já que o que estava nos atrapalhando no denominador sumiu.
E, prontinho. Tá aí nosso limite bonitão!
Resposta
Exercício Resolvido #6
Calcule o limite, se existir.
Passo 1
Bom galera, para começar vamos adaptar um pouquinho! Basta multiplicarmos numerador e denominador por . Lembra daquele papo de multiplicarmos pelo conjugado? Fazemos isso com o objetivo de sumir com aquela raíz dali, afinal ninguém gosta de trabalhar com raiz, né? Então haha
Observa por qual razão fazemos isso
No nosso caso,
Observa que agora conseguimos nos livrar da raíz
Vamos também fazer uma multiplicação distributiva com esse que ta na parte do numerador.
Agora vamos aplicar o limite usando algumas propriedades. E vamos começar com:
Logo o limite pode ficar em cima e embaixo:
Outra propriedade é:
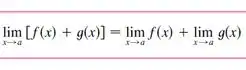
Assim essa parte de baixo cheia de somar pode ficar:
Usando a outra propriedade (kkkkk quantas propriedades). Tudo isso ajuda a gente a manipular nosso limite pra parar em algo que nós consigamos trabalhar sem cair em nenhuma indeterminação. Então lá vai:
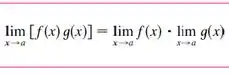
Vamos usar essa pra multiplicação do
Agora vamos usar a propriedade que nos permite trabalhar com o limite dentro da raíz.
Obs: Perceba que só foi possível fazer isso porque a raiz está em todos os elementos dentro do limite.

Gora o grande lance é cortar esse que ainda ta zerando tudo, e para isso vamos aIsolar colocando ele em evidência no denominador:
Agora cortamos o em cima e embaixo ficando com:
Por último
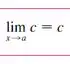
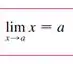
Ufa!!! Aí está esse danado!
Resposta
Exercício Resolvido #7
Calcule o limite:
Passo 1
Olaaaa, vamos continuar nosso estudo!
Então, estudante, se a gente substituir o valor da tendência do na expressão, vai ficar assim:
Bom, isso significa que teremos que achar um outro jeito de solucionar isso.
Passo 2
Vamos lá, repara o seguinte, se zera os polinômios ali, significa então que ele é uma das raízes desse polinômio, né?
Então, vamos abrir esses polinômios aí para poder simplifica-los. O de cima é mais tranquilinho, vamos lembrar de um produto notável, que é diferença de quadrados
Podemos reescrever nosso numerador assim
Agora sim, pegou o bizu? Show! Então temos que:
Passo 3
Matamos o numerador, agora vamos para o denominador, como era esperado o é uma das raízes!
Agora para o denominador (o de baixo), vamos de Bhaskara, lembrando que se temos uma equação desse jeitinho aqui
Que também pode ser
Só mudou a letrinha de para , mas o jeito de resolver é exatamente do mesmo.
Sem problemas!
Achamos as raízes desse jeitão aqui:
Como nossa equação é
Então:
Que nos dá
Assim, as raízes do polinômio serão:
Isso nos dá dois resultados
Simplificando temos
Lembrando que para a equação
Podemos abrir ele com as raízes, e escreve-lo desse jeitinho aqui
Dessa maneira, abrindo o polinômio ele fica assim:
Como temos que , e
Temos
Que nos dá
Passo 4
Reescrevendo agora o polinômio todo com as formas que acabamos de encontrar:
Dá para cortar os né?
Assim deu aquela melhorada né. Daí, é só substituir e ver que bicho dá:
Podemos cortar os do denominador e ficamos com:
E, como menos dividido por menos, dá mais, temos que nosso resultado é
Como esses números não tem raíz, podemos deixar desse jeitinho aí mesmo, que já tá prontinha.
Resposta
Exercício Resolvido #8
Calcule o limite:
Passo 1
Tudo certinho? Tá arrebentando nos exercícios? Então bora partir para um novo desafio!
Como em todo exercício de limite, o nosso primeiro passo deve ser substituir pela tendência de . A tendência de é valer . Logo, temos que substituir por . Mas espera aí! O que aquelas barras que aparecem na parte de baixo do limite significam?

Essas barras são o módulo. O termo da equação é lido como: “o módulo de ”.
E o que o módulo faz de diferente?
O módulo é o seguinte: caso o termo que estiver dentro do módulo seja negativo, o módulo o fará ficar positivo. Mas se o termo que está lá dentro já for positivo, o módulo o manterá positivo.
Mas como ele faz isso???? Vamos ver um exemplinho pra dar aquela clareada nas ideias. Para isso vamos usar outro valor qualquer, tipo o 5:
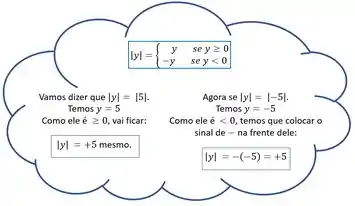
No nosso balazinho, o foi multiplicado por pra ficar positivo, por isso colocamos esse menos na frente dele.
Agora vamos ver como fica para o nosso exercício.
No nosso caso, o termo que está dentro do móludo é o . E saberemos que ele é negativo se ele for menor que zero. Então:
Por outro lado, se o termo que estiver dentro do módulo for maior ou igual a zero, o módulo não faz esse termo mudar!
Agora que entendemos o que o módulo significa, podemos substituir por !
Passo 2
Finalmente fazer a substituição de por ! Só que não!
Como o módulo se comporta de um jeito quando e de outro quando , precisamos fazer se aproximar de pela direita e pela esquerda .
Lembre-se que significa que se aproxima de por valores maiores que :

Lembre-se também que significa que se aproxima de por valores menores que :
Quando , o termo que está dentro do módulo será positivo
Logo ele vai ficar como veio ao mundo:
Quando , o termo que está dentro do módulo será negativo, pois
Logo ele vai ganhar aquele menos na frente:
Passo 3
Depois se lembramos desses detalher, finalmente podemos substituir por e calcular o limite pela esquerda e pela direita, já que teremos que fazer os limites laterais.
Vamos começar com limite pela direita :
Como nesse caso, :
No entanto, ao fazermos as contas descobrimos que o resultado final dá em indeterminação !
Fazendo o limite pela esquerda , e .
No entanto, ao fazermos os cáculos descobrimos que o resultado final dá de novo em indeterminação !
O resultado dessa substituição foi uma divisão por zero . Não é possível dividir um número por zero! Essa divisão é uma indeterminação. Por isso, esse resultado não serve pra gente! No próximo passo vamos descobrir como driblar esse problema.
Passo 4
No passo anterior, vimos que o culpado pela indeterminação é a divisão por zero. Essa divisão só acontece, por causa da parte de baixo da fração (o zero só aparece na divisão por conta de ). Logo, antes de substituir por , temos que nos livrar do debaixo do limite!

Para o desaparecer da parte de baixo da fração, temos que fazer aparecer na parte de cima ! Se a gente fizer isso, vamos poder cortar o debaixo com o de cima! Ou seja, vamos reescrever de forma que apareça.
Fazemos isso através de um produto notável chamado de trinômio quadrado perfeito. Que o carinha que tem esse formatinho aí:
Isso pode funcionar para o nosso caso, porque o termo do limite se parece com o termo do produto notável! Você pode estar achando que os dois não se parecem, mas isso fica mais claro, quando a gente lembra que:
Substituindo isso em , podemos comparar os valover com o produto notável e achar que é e quem é :
Como:
Usando esse produto notável, a gente consegue reescrever e fazer o termo aparecer na parte de cima da fração!
Agora, vamos reescrever o limite e substituir por de novo.
Passo 5
Reescrevendo o limite através do produto notável, achamos:
Cuidado! Lembre que, como o módulo age de forma diferente quando e , precisamos calcular o limite duas vezes: uma vez pela direita e outra pela esquerda .
Começamos então com o limite pela direita.
Cortando o termo que existe em cima e embaixo, achamos:
Agora sim, substituindo por :
Agora, vamos calcular o limite pela esquerda.
Cortando o termo que existe em cima e embaixo, achamos:
Substituindo por :
Enfim, o limite lateral é igual pela esquerda e pela direita. Isso significa que o limite existe e vale !

É isso aí! Mais um exercício concluído, guerreiros!
Resposta
Exercício Resolvido #9
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Faaaala ai! Vamos continuar estudando limites para ficar fera!!
Se substituirmos a gente consegue ver que esse cara vai para uma indeterminação:
Bom, pra fugir disso a gente precisa fatorar esse cara. Mas calma aí, o bagulho tá elevado a ? Como eu faço isso??
Então, você não faz! Mas nós faremos algo que vai nos levar ao resultado, através de um padrão na fatoração.
Passo 2
Para fatorar polinômios de grau maior ou igual a a gente vai usar Briot-Ruffini!
Tendo que o valor é e temos que dividir os dois polinômios por .
Repara ainda, para o polinômio de cima, que teremos acompanhando , em todos do grau até , acompanhando e o acompanhando .
A gente vai pegar esses coeficientes e armar para nossa base do Briot-Ruffini ficar assim:
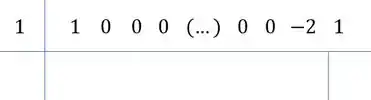
O esquema do Briot-Ruffini :
- Colocar uma raiz no coeficiente (no caso é )
- Colocar os coeficientes
- Desce o primeiro coeficiente
- Multiplica ele pela raiz
- Soma com o próximo coeficiente
- e assim por diante:
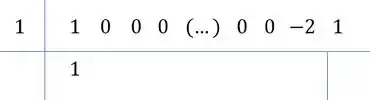
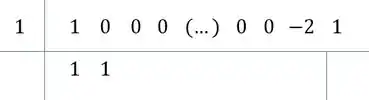
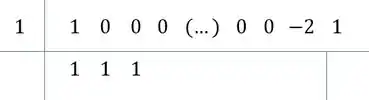
Repara, tem um padrão! Todos com ali vão ter coeficiente ao dividir!
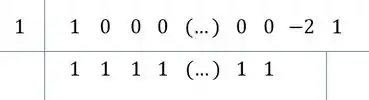
Continuando teremos:
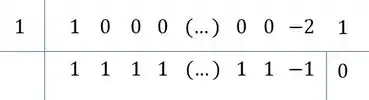
Ou seja, .
Passo 3
Não sei se você já se deu conta, mas para o cara debaixo, com o , vamos ter a mesma coisa! A diferença nesse caso é que os coeficientes zerados estarão só de até .
acompanha acompanha de até , acompanha e acompanha
O esquema do Briot-Ruffini :
- Colocar uma raiz no coeficiente (no caso é )
- Colocar os coeficientes
- Desce o primeiro coeficiente
- Multiplica ele pela raiz
- Soma com o próximo coeficiente
- e assim por diante:
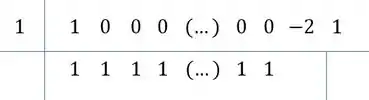
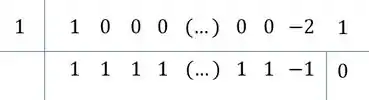
Ou seja,
Passo 4
Substituindo no limite, teremos:
Eiiita, ta feio né?? Podemos cortar o para deixar a situação menos pior kk ficando com:
Rapaz, repara nesse limite que sobrou! Lembra que elevado a qualquer número vai dar ? A gente vai ficar com números em cima e embaixo ao substituir , fora os dois que sobraram ali:
E isso fica
Simplificando, temos:
Questão trabalhosa e complicadinha, hein?
Resposta
Exercício Resolvido #10
Calcule o limite:
Passo 1
Opa fala aii! Vamos continuar com nossos limites!
A gente começa substituindo o limite, certo?
Deu ruim né? Então, vamos tentar dar um jeitinho algébrico.
Passo 2
Zerou em cima e embaixo, o que significa que vai aparecer na fatoração dos dois termos.
Vamos dividí-los por esse termo, o de cima por Briot-Ruffini, o de baixo por Bhaskara.
Começamos com o de baixo, que é mais tranquilo
Para achar quem é e vamos lembrar da nossa forma da equação do segundo grau
E nossa equação é
Então temos que
Colocando isso no nosso Bhaskara, temos
Então temos duas raízes
Simplificando, temos que
Lembrando que para a equação
Podemos abrir ele comas raízes, e escreve-lo desse jeitinho aqui
Dessa maneira, abrindo o polinômio ele fica assim:
Como temos que , e
Temos
Passo 3
O de cima, dividimos ele por pelo método de Briot-Ruffini, lembrando que a gente tem um esquema para fazer esse Briot-Ruffini ai,
O esquema do Briot-Ruffini :
- Colocar uma raiz no coeficiente
- Colocar os coeficientes
- Desce o primeiro coeficiente
- Multiplica ele pela raiz
- Soma com o próximo coeficiente
- e assim por diante:
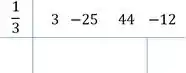
Desce o primeiro coeficiente:
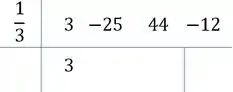
Multiplicamos a raiz pelo primeiro e somamos ao segundo:
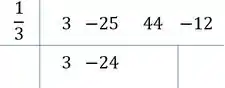
Repetimos isso para os dois outros números que restam:

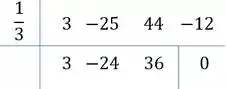
Ou seja,
Passo 4
Substituindo no limite:
Podemos cortar esse e ficamos com:
Aaaaaaaaaaah agora sim, podemos substituir felizes!
Dando uma penteada nele, ficamos com
Simplificando isso daí, temos
Fazendo essas somas, temos
Na divisão de 2 frações, repetimos a primeira e multiplicamos pelo inverso da segunda:
Aplicando o MMC, achamos que:
Que dá
Simplificando, temos