Limites no Infinito
Teoria
Fala aí! Chegamos a mais um passo rumo à nossa tão sonhada formação, e está na hora de vencer os limites no infinito. Vem com a gente que vou te mostrar como.
Já sabemos como resolver vários tipos de limite. Lembrando que o primeiro passo é substituir a tendência do na função que queremos calcular o limite.
Agora imagina que você se depara com essa questão aqui:
A princípio parece tudo bem, mas quando você vai fazer a substituição, você percebe que o está tendendo para o infinito.
E não há problema nenhum nisso, apenas quer dizer que o é um valor muito, muito, muito grande, tão grande que vai para o infinito. Então, nós faremos o mesmo que já sabemos fazer. Nós substituímos a tendência do e vemos o que vai acontecer.
Tiramos o operador e trocamos o por , ficando com:
Mas o que significa?
Bom, pensa só. O infinito é algo muito, muito, muito grande, certo? E o que estamos fazendo ali é uma divisão, dividindo o 3 por esse tal infinito gigantesco. O que isso vai dar?
Pra imaginar isso de uma forma mais prática. Imagina que você tem três maçãs e vai tentar dividir essas maçãs com três pessoas:

Assim a divisão seria: maçã para cada pessoa.
Agora imagina que vamos dividir essas mesmas três maçã com seis pessoas:

Para que todos ganhem, teremos que dar a metade da maçã para cada um, assim a divisão seria: . Uma metade para cada.
Se agora quisermos repartir nossas três maçãs entre 12 pessoas? Você concorda que o pedaço que cada uma ganhará corresponderá a de maçã?

Seguindo esse ritmo vemos que quando dividimos um número por um valor muito grande, essa divisão tem resultado bem pequeno.
Assim, quando dividimos uma constante por um número que tende ao infinito, essa divisão tende a zero, pois ninguém poderá saborear esse pedacinho tão pequeno da maçã.
Nesse caso dizemos que:
Essa ideia ajudará bastante, então vamos sintetizar isso com esse limite aqui:
Ou seja, uma constante dividida por infinito vai a zero.
Quociente de funções com
Não pense que todo limite com indo ao infinito vai a zero. Isso vai deperder muito da função.
Vamos ver alguns casos:
-
Substituindo o limite teremos:
Opaaaa!!! Isso aí não pode não, produção!!!
Nosso limite caiu em uma indeterminação do tipo . Quando isso acontece, nós temos que voltar a nossa função e mexer um pouco nela para torná-la mais calculável, e aí sim aplicar o limite.
E aqui vai uma informação muito importante. Olha só: limites com divisão de polinômios indo a a gente pode sempre resolver do mesmo jeito, nós colocamos o termo de maior grau em evidência em cada polinômio. No nosso caso, o termo de maior grau do numerador é o , e do denominador é o .
Vamos colocar eles em evidência multiplicando e dividindo cada termo dos polinômios por eles. Assim:
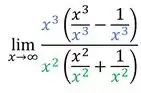
Fazendo isso nós poderemos simplificar as divisões:
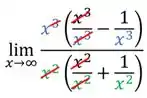
Repara que do lado de fora dos parênteses podemos cortar o com o , mas ainda sobra na parte de cima. Ficando com:
E isso é muito bom, pois poderemos aplicar o limite diretamente e teremos alguns divisões por infinito. E já vimos ainda agorinha que elas irão a zero . Assim:
Essas divisões por infinito vão a zero:
E ficamos com:
Assim:
Prontinho!
Com isso concluímos que não é porque a parte de cima e a de baixo tendem ao infinito que elas crescem igualmente. O , cresce bem menos que . E é por isso que esse limite está divergindo para o infinito.
-
Vamos ao próximo exemplo:
Aplicando o limite diretamente, teremos:
O que não pode acontecer, então vamos arrumar isso aí colocando o de maior grau de cada polinômio em evidência:
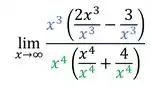
Assim, poderemos cortar:
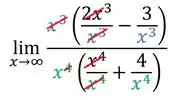
Repara que do lado de fora dos parênteses podemos cortar o com o , mas ainda sobra na parte de baixo. Ficando com:
Todos os termos com no denominador zeram quando lembra? Quando dividimos um valor por algo muito, muito muuuuuuuito grande o resultado será muito pequeno, indo a zero. Então aplicando o limite vai ficar:
Assim, chegamos ao resultado:
Agora vamos ver um outro caso:
Aplicando diretamente o limite teremos uma indeterminação do tipo . Então já sabe, né. Bora colocar o de maior grau em evidência em cada polinômio:
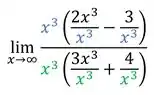
Cortando:
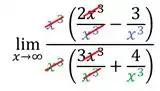
Como os graus de fora dos parênteses eram os mesmos, não sobrou nenhum do lado de fora.
Ficamos com:
Aplicando o limite:
Prontinho, limite calculado. Assim:
Resumindo:
Você reparou nos exemplos que escolhemos e o que aconteceu com cada um deles? Eles eram esses aqui:
Um quociente entre polinômios onde o grau do de cima é maior que o grau do de baixo.
E o resultado foi igual a infinito.
Esse é um quociente entre polinômios onde o grau do de baixo é maior que o grau do de cima.
E o resultado foi a zero
Esse é um quociente entre polinômios de mesmo grau. E o resultado do limite foi igual ao quociente dos valores que acompanhavam o termo de maior grau em cada polinômio.
Esses resultados são resultado que sempre vão ter esse comportamento. Então, não precisamos ficar calculando o limite toda vez. Podemos diretamente olhar essa relação entre o grau de cada polinômio. Seguindo o esqueminha a baixo que é pra levar por coração:

Com esse esquema em mão, vamos para os exercícios.
Quociente de funções com x → ∞
Resumindo:
Exercícios Resolvidos
Exercício Resolvido #1
Encontre o limite
Passo 1
E aí, tudo beleza?
Vamos ver esse limite aí!
A função que a gente tem que aplicar o limite é uma raiz quadrada, e nela faremos o tender ao infinito. Ou seja, vamos fazer essa valor de se tornar muito, muito, muuuuuuito grade.
Pensa o seguinte: quanto maior o número que tá dentro da raiz, maior vai ser o resultado dessa raiz né?
Vamos ver o que acontece quando esse número vai aumentando. Olha só:
Se ali dentro aumentar, o resultado da raiz também aumentará!
Então vamos dar uma olhada no que tá dentro da nossa raiz aqui!
Passo 2
Chamamos de radicando o número que está dentro da raiz.
No nosso limite:
O nosso radicando aqui é:
Quanto maior for o valor de , maior vai ser o valor de !
Então, à medida que o nosso aumenta, indo pro infinito, também vai pro infinito!
Passo 3
Consequentemente a nossa raiz também vai pro infinito😉
E assim podemos determinar nosso limite.
Ou seja...
E prontinho! Limite calculado! Uhuul!
Resposta
Exercício Resolvido #2
Encontre o limite
Passo 1
Olá! Tudo joia? Vamos ver mais esse limite que tem o indo pro infinito? Bora!
Olha só, se a gente tentar substituir aqui, vamos ter:
Isso aqui é tipo de indeterminação! Então a gente não pode ir por esse caminho...
E agora?
Calma, vem comigo!
Passo 2
Vamos fazer uma modificaçãozinha aqui...
Lembra que , então a gente pode reescrever o limite como:
Como nós temos em todos os termos, vamos colocar o em evidência. Pra isso, colocamos o multiplicando “do lado de fora”, abrimos os parênteses e dividimos todos os termos por . Assim:
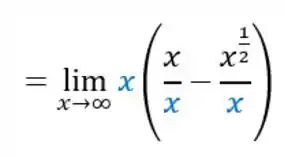
Passo 3
Na parte de dentro dos parênteses nós temos agora duas divisões, o que é igual a , e o onde a gente vai precisar usar uma propriedade de potenciação que diz que: na divisão de potências de bases iguais, a gente repete a base e subtrai os expoentes!
Vamos fazer isso separado aqui pra gente ver melhor como fica.
Lembrando que quando não tem nada do expoente a gente acrescenta o 1:
Temos essa continha no expoente pra resolver, então vamos escrever o como sendo pra que ele fique com o mesmo denominador que o :
Agora a gente resolve em cima e repete em baixo, ficando com:
Show, está quase bom. Pra ficar ainda melhor vamos ajeitar esse expoente aí que está negativo, jogando ele pra baixo pra ficar positivo. Assim ó:
E escrever ele em forma de raiz:
Beleza! Vamos encaixar isso no nosso limite agora😉
Passo 4
Nosso limite era assim:
E então fica assim:
Como agora tem uma multiplicação de por , a gente pode separar esse limite assim:
Vamos prestar atenção nesse pedacinho aqui:
Veja que a medida que aumenta, a raiz também aumenta, olha só:
Consequentemente, a divisão vai diminuir, pois vamos dividir o por um número cada vez maior...
Com isso, esse pedacinho: tende a zero, quando tende a infinito.
Passo 5
Entendendo isso, podemos aplicar agora podemos aplicar o limite na nossa função, e chegamos no seguinte:
E esse é o resultado do nosso limite!
Resposta
Exercício Resolvido #3
Encontre o limite
Passo 1
E aí, tudo joinha?
Vamos ver esse aqui que é um caso um pouquinho especial!
Essa função é uma velha conhecida nossa né? Vamos lembrar um detalhezinho dela...
Lembra da imagem dessa função? Vem comigo...
Passo 2
Vamos dar uma olhada no gráfico dessa função pra a gente entender melhor o comportamento dela:
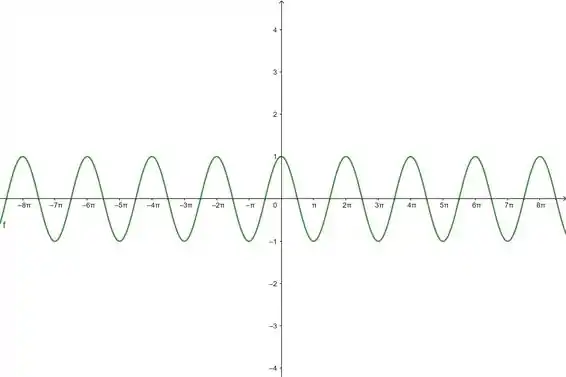
Pelo gráfico a gente consegue ver que a função é periódica, variando de a . Tranquilo?
Passo 3
Beleza, que conclusão a gente chegou então?
Conforme aumenta, a função cosseno não se aproxima de nenhum valor específico, porque ela sempre oscila entre e . Ou seja, esse limite aqui:
Não existe! Já que a gente não consegue definir um valor específico pra onde essa função está indo.
Então, a gente responde assim mesmo, dizendo que esse limite não existe usando o símbolo ()😉
Resposta
Exercício Resolvido #4
Propriedades dos Limites
Calcule o limite ou prove que não existe:
Passo 1
Opa! Tudo bem?
Ao aplicarmos o limites nessa função vamos ter:
O que é uma indeterminação, então vamos procurar outro jeito pra resolver essa questão.
E aqui vai uma informação muito importante. Olha só: limites com divisão de polinômios indo a a gente pode sempre resolver do mesmo jeito, nós colocamos o termo de maior grau em evidência em cada polinômio. No nosso caso, o termo de maior grau é o .
Vamos colocar ele em evidência multiplicando e dividindo cada termo por . Tanto no polinômio que tá em cima, quanto no que tá embaixo.
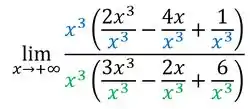
Agora a gente simplificar as frações que ficaram dentro dos parêntes:
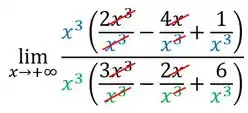
Como isso, ficaremos com:
(Lembrando que quando dividimos potências de bases iguais, repetimos a base e subtraímos os expoentes, por isso: por exemplo)
Passo 2
Agora podemos cortar o em cima e embaixo:
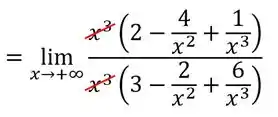
Ficando com:
Já melhorou bastante assim, agora podemos aplicar o limite novamente e ver se conseguimos um resultado que não caia em indeterminação novamente.
Todos os termos com no denominador zeram quando , lembra? Quando dividimos um valor por algo muito, muito muuuuuuuito grande o resultado será muito pequeno, indo a zero. Então aplicando o limite vai ficar:
E prontinho! Limite calculado! Viu como aquela dica de colocar o termo de maior grau dos polinômios em evidência salvou a gente? Então, guarda ela pra usar sempre que precisar! 😊
Resposta
Exercício Resolvido #5
Determine o limite abaixo
Passo 1
Opa! Bora ver mais esse?
Substituindo diretamente o limite, temos uma indeterminação:
Então a gente não pode ir por esse caminho, vamos pensar de outra forma...
Passo 2
Pra começar vamos separar esse limite em duas partes, já que temos uma soma de duas frações ali:
E vamos resolver esse aqui primeiro:
Temos aqui uma divisão de dois polinômios. Agora presta atenção no grau desses polinômios: o termo que tem maior grau em cima é o , e embaixo é o . Então, a gente vai colocar eles em evidência multiplicando na frente, abrimos os parentes e dividimos cada termo do polinômio pelo termo de maior grau que a gente acabou de colocar em evidência. Vem comigo que vou lhe mostrar!
Passo 3
Vamos colocar o em evidência em cima e o em evidência na parte de baixo:
Não esquece de dividir cada termo que vai ficar dentro dos parênteses pelo que foi pra evidência, assim ó:
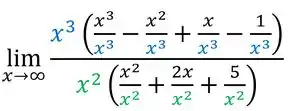
Podemos simplificar as frações que estão dentro dos parêntese:
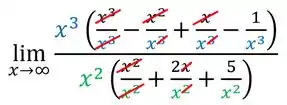
Simplificamos essas frações, diminuindo os expoentes, e vamos ficar com:
A gente pode ainda, simplificar o como o que estão na frente dos parênteses, diminuindo os expoentes pra ficar com:
Passo 4
Agora a gente pode separar isso em um produto:
Essa primeira parte dá infinito, certo?
E a segunda?
Bom, lembra que toda constante dividida por uma potência de , com dá zero?
Ou seja:
Passo 5
Olhando pro nosso limite então, todos aqueles termos com no denominador vão pra zero. Ou seja:
Juntando esse dois limites, temos:
Passo 6
Beleza! Vamos para aquele outro limite que estava somando lá no início, o:
Vamos fazer do mesmo jeito que o outro, só que aqui a gente vai colocar o em evidência em cima e embaixo, por ser o termo de maior grau...
Simplificando:
E podemos cortar o porque ele tá multiplicando em cima e embaixo, assim ficaremos com:
E como a gente já viu, todos os termos com no denominador vão pra zero, então...
Show, já temos o resultados dos dois limites.
Passo 7
O que ele pediu no enunciado foi o limite dessa soma:
E agora juntando o resultado dos limites, temos:
E acabamos por aqui! 😉
Resposta
Exercício Resolvido #6
Calcule o limite:
Passo 1
Vamos ver mais essa aqui!
Substituindo diretamente o limite, nós caímos em uma indeterminação:
Não dá pra a gente fazer assim então. Vamos ver pelo meio da fatoração!
Passo 2
Para essa fração, o maior grau de cima é e de baixo é . Vamos coloca-los em evidência (dica: podemos fazer isso de um jeito bem direto, subtraindo cada expoente pelo grau do termo que estamos colocando em evidência). Veja
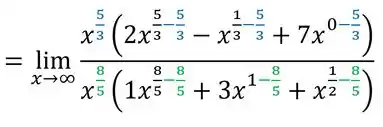
Vamos fazer agora aquelas subtrações ali nos expoentes com as frações...
Passo 3
A primeira subtração em cima é:
Depois
Aqui os denominadores são iguais, então a gente pode subtrair em cima e repetir o denominador:
A próxima que trava o nosso caminho é:
Aqui a gente pode escrever pra poder ficar com os mesmos denominadores
Agora falta:
Pra ficar com denominador igual, a gente pode multiplicar o por em cima e embaixo e o por :
Prontinho! Vamos jogar isso lá no limite agora!
Passo 4
Voltando aqui:
(Lembra que o negativo do expoente a gente pode eliminar jogando ele pra baixo)
Agora vamos simplificar esse que está na frente do parêntese em cima, com o na parte de baixo, também diminuindo os expoentes...
Passo 5
Olhando só para esses expoentes. Vamos fazer aqui:
Temos que deixar com denominadores iguais, então a gente pode multiplicar por em cima e embaixo, e por :
Reescrevendo lá então...
Passo 6
Vamos separar essa multiplicação assim agora:
Olha esse primeiro:
Passo 7
Beleza, o primeiro deu infinito, e o segundo?
Todos os termos com no denominador, com vão pra zero, lembra? Então aqui vai ficar:
Então...
Passo 8
Nosso limite é:
E finalmente, limite calculado! 😊
Resposta
Exercício Resolvido #7
Calcule o limite abaixo:
Passo 1
Vamos lá?
Se começarmos substituindo o valor do limite, encontraremos um problema. Vai ficar com infinito sobre infinito, o que é uma indeterminação ☹:
Vamos tentar outro jeito então...
Passo 2
A saída melhor para essa situação é, a gente perceber que dentro de cada raiz temos um polinômio, então podemos tentar colocar o maior grau desses polinômios em evidência.
Perceba que o maior grau da função de cima é, e da função de baixo é , então bora botar a maior potência de de cima e de baixo para fora.. Fica assim:
(quando a gente coloca um termo em evidência, dividimos todos os termos por ele)
E agora a gente simplica os expoentes ali de dentro, diminuindo o de cima pelo de baixo...
Passo 3
O próximo passo é tirar os nossos e ali de dentro das raízes.
Pra fazer isso nós cortamos o expoente da potência de como o índice da raiz, e então o pode sair da raiz e ir pra frente dela multiplicando.
Ah, só mais um detalhe, quando a gente tira uma potência de de dentro de uma raiz par (raiz quadrada, quarta, sexta, e assim por diante) temos que colocá-lo em módulo, ok.
Então ficaremos com:
Passo 4
Nesse caso, temos , pois trabalhamos com tendendo a um valor positivo, já que :
Como temos multiplicando embaixo e em cima, podemos cortar e ficaremos com:
Passo 5
Agora, como , todos os termos com no denominador vão pra zero, lembra?
Então, aplicando o limites vamos ter isso aqui:
E pronto! Esse é o nosso limite😉
Resposta
Exercício Resolvido #8
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Opa! Vamos ver esse limite cheio de raízes aí! Sem pânico! Vamos lá...
Substituímos de início:
Opss... isso é uma indeterminação, então a gente não pode ir por esse caminho...
Mas vamos seguir...
Passo 2
Para esse cara, notamos que o maior grau é o mesmo em cima e embaixo, é esse dentro da raiz quadrada. Vamos colocá-lo em evidência.
Aí lembra que . Assim vamos ter:
Simplificando:
Que voltando pra forma de raiz, fica:
Passo 3
Como a gente tá multiplicando o e o dentro da raiz de cima, e e dentro da raiz de baixo, a gente pode abrir essas raízes colocando uma raiz pra cada pedaço das multiplicações que estão dentro delas. A gente faz isso aqui:
Com isso, podemos cortar essa em cima e embaixo, ficando só com:
Passo 4
Nós já aprendemos que todo termo com no denominador, quando , vai a zero. Ou seja, todos aqueles termos ali onde tem no denominador, vão zerar:
Então, aplicando o limites, teremos:
E pronto! Calculamos mais um limite! 😊
Resposta
Exercício Resolvido #9
Calcule o limite, caso exista. Caso não exista, justifique.
Passo 1
Opa! Esse confundiu um pouco né? O que são aquelas reticências ali?
Aquilo ali quer dizer que temos uma progressão, com oito termos da forma , onde o tá indo de .
Se fossemos escrever todos eles, ficaria assim:
Bem grande né? Então nós podemos colocar as reticências para não termos que escrever todos eles o tempo todo, mas precisamo sempre lembrar quem são os termos que estão ali, ok.
Beleza, como resolver isso?
Em primeiro lugar, ao substituir o limite de , vamos ter uma indeterminação Nenhuma novidade até aí:
Então, o jeito é tentar resolver de outra forma.
Passo 2
Vamos analisar o grau de cada polinômio (o de cima e o debaixo).
Embaixo, temos um polinômio de grau , isso porque ao desenvolver o polonômio, teremos um termo com .
Vamos colocar o e evidência em cada polinômio que temos.
Bom, se por um padrão colocarmos todos os dos parênteses de cima em evidência, quantos seriam?
Um para cada termo multiplicando, ou seja, termos ! Esses termos multilplicados, vão nos resultar em como termo de maior grau também, entendeu?
Ou seja, vamos colocar em evidência em cima e embaixo...
Passo 3
Assim ó:
Agora podemos cortar o em cima e embaixo:
Passo 4
Lembra que todo termo com no denominador, quando dá zero?
Então, aplicando o limites:
E... acabamos mais esse😊
Resposta
Exercício Resolvido #10
Determine onde .
Passo 1
Esse complicou mais um pouco né? Mas calma, vamos devagar que sai...
Para simplificar o trabalho de calcular podemos primeiramente ver o que acontece com calculando o valor de e ver quando a gente acha...
Bora?
Passo 2
Calculando:
Vamos aplicar a distributiva ali:
Vamos colocar o termo de maior grau em evidência agora, em cima e embaixo:
Podemos agora cortar o em cima e embaixo:
Passo 3
A gente já sabe que todos os termos com no denominador, sendo que , vão pra zero. Então aplicando o limites...
Beleza, agora vem comigo!
Passo 4
A gente já fez:
Ou seja, vimos que quando tende ao infinito, tende a 2. E como o nosso limite é:
Basta a gente calcular:
Beleza?
Passo 5
Vamos focar nesse limite então:
Percebe que se a gente substituir , teremos:
E quando acontece de zerar só o denominador, não temos como fatorar. Vamos analisar então os limites laterais...
Passo 6
Vamos ver os limites laterais desse cara:
Ou seja, o limite vai pra menos infinito tanto pelo lado direito, quanto pelo lado esquerdo!
Esse limite então vai para no final das contas😉
Resposta
Exercício Resolvido #11
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Obs: considere
Passo 1
E aí, tudo joia?
Se a gente substituir aqui, vamos chegar numa indeterminação, então a gente não pode ir por esse caminho...
Vamos tentar chegar num produto aqui pra dar certo, beleza?
Passo 2
Vamos começar a reescrever o que tá ali dentro assim:
Percebe que nos dois a gente tem ? Então a gente pode colocar esse termo em evidência, bora lá? Vai ficar assim:
Passo 3
Então a gente pode reescrever nosso limite assim:
Temos ainda, pela propriedade do produto:
Vamos ver cada um desses limites agora!
Passo 4
Vamos ver esse primeiro:
Aqui o resultado dependerá do grau de ser par ou ímpar, vamos achar um resultado para cada tipo de . Não entendeu? Vem comigo!
Para ímpar, teremos par, certo? Então olha só:
E para par, teremos ímpar. E aí...
Ok, isso por enquanto, beleza?
Passo 5
Vamos ver esse limite aqui agora:
Esse aqui é mais fácil, só substituir ali e a gente vai fcar com:
Então a gente pode aplicar isso junto com os dois casos ali de cima, vem comigo!
Passo 6
- Para ímpar:
- E para par:
Beleza! Esses dois casos já foram!
Passo 7
O único caso fora desses é o caso com . Repara só, vamos colocar na expressão do limite, ficamos com:
Então a gente tem esses três casos para o limite! E encerramos por aqui 😉