Limites Laterais e Continuidade
Teoria
Limites Laterais
Você se lembra da ideia fundamental do cálculo de um limite? O que significa calcular o seguinte limite?
Bom, o que esse limite está perguntando pra gente é de qual o valor a função se aproxima quando fazemos o tender a .
A ideia aqui é ir aproximando o do valor o máximo possível, e nós podemos fazer isso de duas maneiras diferentes: por valores menores que , ou por valores maiores que .
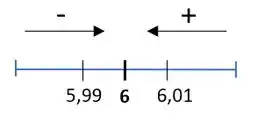
Imagine uma reta numérica, onde estamos nos aproximando do número .

Agora vamos construir uma tabela e calcular os valores da função para cada valor de escolhido, tanto para os valores menores (que se aproximam de pela esquerda), quanto pelos maiores (que se aproximam de dois pela direita).
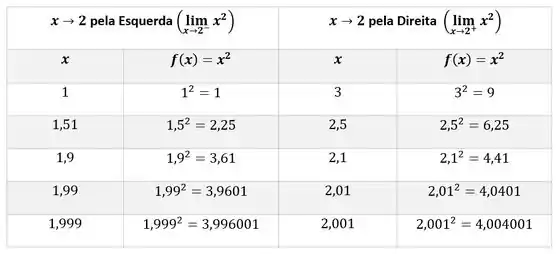
Quando nos aproximamos do pela esquerda, a função vai ficando cada vez mais próxima do , com valores menores que , mas muito próximo dele. E quando nos aproximamos do pela direita, a função vai ficando cada vez mais próxima do , com valores maiores que , mas muito próximos dele.
Assim a gente define os limites laterais:
e
Para indicar que estamos nos aproximando do por valores menores que , escrevemos embaixo do limite, esse sinalzinho de menos em cima do indica que são valores menores que ele. E para indicar que estamos nos aproximando do por valores maiores que , escrevemos , onde o sinalzinho de mais em cima do indica que são valores maiores que ele.
Então, esses são os limites laterais, como eles são iguais, constatamos que o limite geral da função é .
Limites Laterais Diferentes:
Nem sempre os limites laterais serão iguais. Imagine a seguinte função:
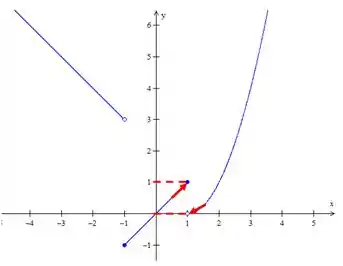
Essa é uma função dado por partes. Então, para os valores de ela se comporta como a parábola , mas para valores de ela será descrita pela função exponencial .
Observe o gráfico dela:
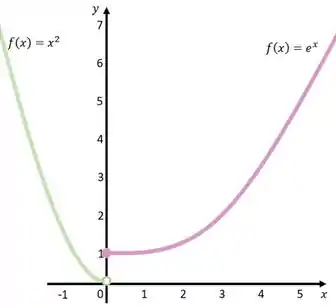
Veja o que acontece com a função próximo do ponto :
Se você tentar aproximar o a zero, vamos ter um probleminha. Você pode ver que a função tem tendências diferentes naquele ponto. Pela esquerda, ela é o . Pela direita, é . Daí surge uma pergunta: queremos aproximar por onde? Pela esquerda ou pela direita?
Se aproximarmos do número por valores menores que , ou seja, pela esquerda, estamos tendendo a. Aí usamos a notação com o “” em cima do zero, e precisaremos usar a função , já que essa é a função que está definida para valores menores que .
Da mesma forma, se aproximarmos de um número por valores maiores que , ou seja, pela direita, estamos tendendo a. Assim, usamos a notação com “”, mas aqui a parte da função que deve ser usada é o .
Voltando ao desenho do gráfico, você vai perceber que a tendência do limite quando observarmos pela esquerda é ir para . Já a tendência pela direta será a de ir para .
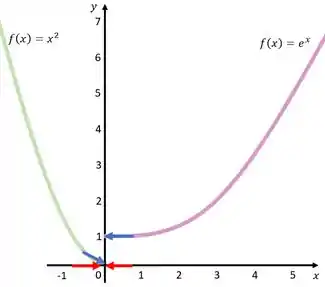
Então, vemos que nem sempre os limites laterais são iguais.
Existência do Limite
No exemplo anterior, vimos que os limites laterais não batem!
Mas se os limites laterais são diferentes, o que acontece com o limite geral em questão? Ele é ou é ?
Nesse caso, dizemos que o limite NÃO EXISTE!
Para que um limite existe ele precisa respeitar duas regras:
Limites laterais não podem explodir para .
Limites laterais devem possuir o mesmo valor.
Apenas quando os limites seguem essas duas condições é que podemos afirmar que o limite existe.
No exemplo inicial, os limites laterais não explodem para , respeitando a primeira condição. Porém, eles não convergem para o mesmo valor, eles são diferentes:
Logo o limite não vai existir! De maneira geral, um limite existe se:
Agora que já pegamos essa ideias da existência do limite, vamos conversar um pouquinho sobre a continuidade de uma função.
Continuidade
Dá uma olhadinha nesses dois gráficos aqui: 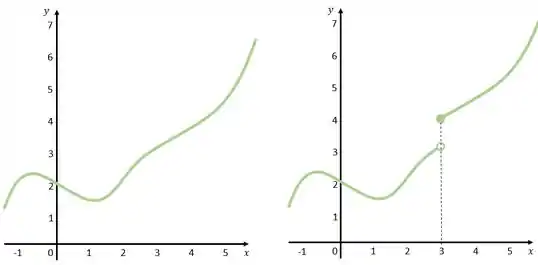
Eles são até muito parecidos. Mas a função da direita dá um salto no indicando uma descontinuidade nesse ponto da função.
Podemos pensar também que uma função contínua tem todos os pontos do gráfico bem “grudadinhos” um no outro. Para desenhá-la não precisaríamos tirar o lápis do papel. Já para representar uma função descontímua, teriamos que seprar esse gráfico no ponto de descontinuidade, tirando o lápis do papel na hora de desenhar. Vamos ver outros exemplos:
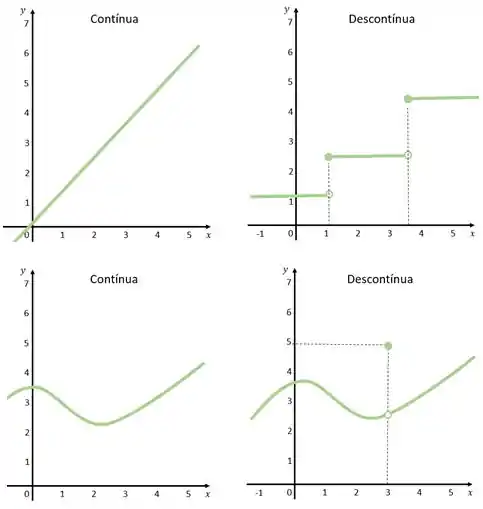
Visualemente é fácil de saber quando uma função é contínua ou não, mas nem sempre temos o gráfico pra ajudar a gente com isso. Então, podemos determinar se a função é contínua ou não através da definição que veremos agora.
Definição de Continuidade
Mas como provar matematicamente que uma função é ou não contínua?
Quem vai ajudar nessa tarefa será o limite. Para que uma função seja contínua, o limite da função precisar ser exatamente igual a própria função em todos os pontos do seu domínio. Podemos resumir em três condições de existência:
Uma função é contínua num ponto quando:
- A função está definida nesse ponto:
- O limite da função existe nesse ponto:
- O limite da função é igual a própria função:
Bom, uma das coisas que precisamos é que o limite da exista! Vimos que isso só acontece quando os limites laterais são iguais:
Mas essa condição não é suficiente. Lembra desse gráfico aqui?
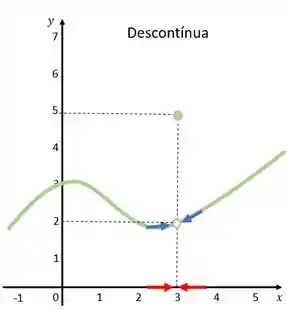
Vemos que os limites laterais para tendendo a levam a função para o , mas o valor da função no ponto é igual a .
Temos uma interrupção, assim, dizemos que:
A função é descontínua no ponto em que , pois se jogarmos o limite
Mas . E é por isso que precisamos que a função seja igual ao limite, para que haja continuidade.
CUIDADO, ter limites laterais iguais não quer dizer que a função é contínua.
Onde Procurar as Descontinuidades?
Cara, pensa comigo, uma função tem infinitos pontos. Para que ela seja contínua ela precisa respeitar a condição de continuidade em todos os pontos. Mas, como vamos fazer o teste para todos eles?
Bem, você não vai precisar testar todos os pontos! Existem funções que são sempre contínuas em seus domínios. Essas funções são:
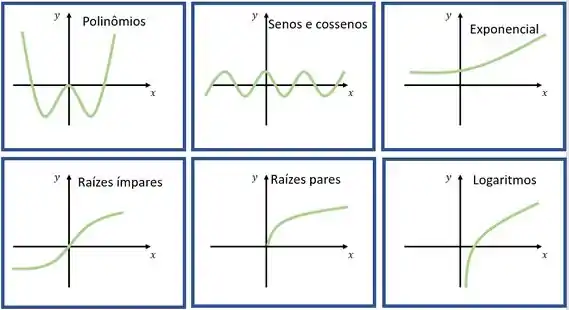
- Polinômios, para todo .
- Funções seno e cosseno, para todo .
- Funções exponenciais, para todo .
- Funções raízes ímpares, para todo .
- Funções raízes pares para
- Funções logarítmicas, para todo .
Essas são as que mais aparecem, e já podemos “de cara” considerar que elas são contínuas.
As descontinuidades podem surgir em pontos que não estão definidos no domínio de uma função, ou no limite entre as em funções dadas por partes. Vamos ver alguns exemplos pra isso ficar mais claro:
Exemplo:
- Encontre os pontos de descontinuidade da função
- Determine se a função a baixo é contínua:
Para que a função seja contínua ela precisa estar definida em todos os pontos, então vamos avaliar o domínio.
Como a função é um quociente, o denominador não pode zerar. E isso acontece quando , pois ficaríamos com:
Como não podemos fazer uma divisão por zero, concluímos que o é um ponto de descontinuidade, pois a função no ponto não existe.
Veja que essa função é dada por partes, assim o gráfico dela será a parábola para valores menores que , e a reta para valores maiores ou iguais a .
Os dois pedaços dessa função são funções naturalmente contínuas, nesse caso o problema pode estar no ponto de troca entre elas que é o ponto . Assim vamos avaliar as condições de continuidade para esse ponto:
Como o ponto é , usaremos a condição da função ser , pois essa é a regra para valores maiores ou iguais a Assim:
Então sim, a função está definida nesse ponto e é igual a .
Para saber se o limite existe, teremos que fazer os limites laterais próximos a esse ponto:
Para fazer precisaremos pegar a parte da função que é descrita por , pois estaremos nos aproximando de por valores menores que ele. Assim:
E para fazer precisaremos pegar a parte da função que é descrita por , pois estaremos nos aproximando do por valores maiores que ele. Assim:
E os limites laterais deram valores diferentes o que mostra que o limite não existe nesse ponto. Isso indica que o ponto é um ponto de descontinuidade.
Como o limite não existe, a última condição também não será satisfeita.
Logo, nossa função é descontínua no ponto .
Também podemos ver isso através do gráfico da função:
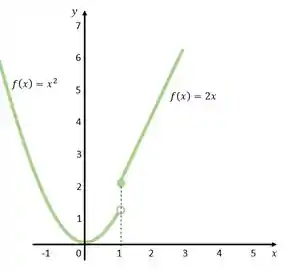
Viu o ponto de descontinuidade bem ali no ? Do jeitinho que a gente viu através dos cálculos!
E pra ficar fera nessa matéria, bora pro exercício!
Limites Laterais Diferentes:
Existência do Limite
Continuidade
Definição de Continuidade
Onde Procurar as Descontinuidades?
Exercícios Resolvidos
Exercício Resolvido #1
Calcule os seguintes limites laterais:
Passo 1
Faaala aii, tudo show de bola?! Na hora de resolver um limite, normalmente,
substituímos o valor de da função pelo valor que ele está tendendo no limite, para termos uma ideia do que acontece. Fazendo isso aqui, ficamos com:
Putz, e agora? No caso dos limites laterais o buraco é mais em baixo, porque aqui quando o denominador se aproxima de zero, a fração tende para o infinito.
Mas afinal, qual é a resposta certa? Precisaremos analisar o limite para os dois casos, tanto quando quanto quando .
Passo 2
No caso dos limites laterais, vamos analisar o comportamento pelos dois lados do . Ou seja, vamos ver como a função se comporta quando se aproximar do pelo lado direito, tipo ou pelo lado esquerdo, tipo
Isso faz com que o denominador resulte em algo um pouquinho maior ou um pouquinho menor que . Vamos olhar para um lado de cada vez.
Passo 3
Se a gente começar olhando para o lado esquerdo (), substituindo o temos:
E quanto mais eu me aproximar do menor esse número vai ficar:
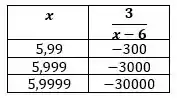
Até que ele se torne um infinito negativo!
Passo 4
Agora, substituindo pelo lado direito , por exemplo, com na função, ficamos com:
Repara que aqui quanto mais perto do eu chegar, menor vai ser o valor no denominador se aproximando do zero e fazendo com que a fração vá para o infinito, mas dessa vez positivo.
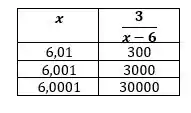
Logo, a diferença vai ser apenas no sinal.
Passo 5
Então, do lado direito tendemos para e do esquerdo . Ou seja,
Ainda não acredita? Então dá uma olhada no gráfico:
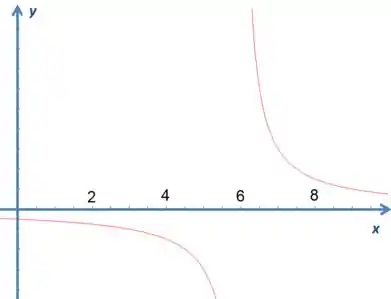
Resposta
Exercício Resolvido #2
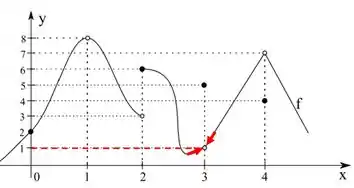
Considere a função definida pelo gráfico abaixo.
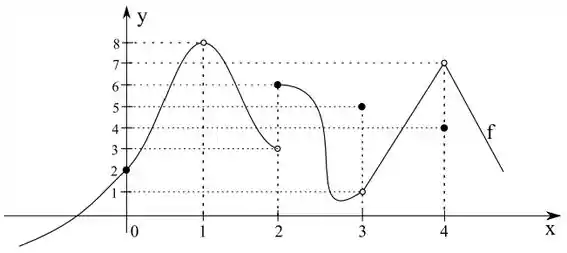
Determine o para se existir
Passo 1
Opa,tudo bom?? Vamos seguir com nossos estudos para aprender tudinho de limites laterais!
Vamos lembrar um pouco da teoria. Dizemos que um limite tem um certo valor , se
“E o que que isso quer dizer???” basicamente isso diz pra gente que o limite (que nesse caso vale ) existe se os limites laterais são iguais!
Então, o que teremos que fazer aqui é verificar os limites laterais em cada ponto.
Passo 2
Vamos começar com o ponto .
Se seguirmos o gráfico com o dedo pela esquerda até chegar a zero, vemos que:
Agora se fizermos a mesma coisa, seguir o gráfico com o dedo pela direita até chegar em zero, encontramos que
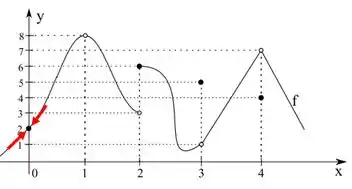
Ó que coisa boa, tanto pela esquerda quanto pela direita, o limite deu , isso quer dizer que o limite existe e vale
Passo 3
Vamos repetir para . Mas a função não está definida ali, já que temos uma bolinha aberta!!
Isso não importa, o limite só está interessado na tendência da função e não no valor no ponto. Então, pelo gráfico
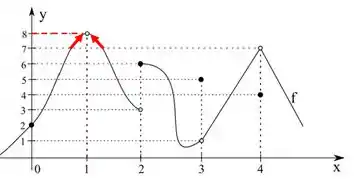
Assim,
Passo 4
Vamos repetir para . Aqui vamos analisar o gráfico com cuidado.
Se percorremos a função pela esquerda, temos que ao chegar em que está na altura então podemos concluir que
Agora, se formos pela direita, vamos chegar numa altura diferente, logo o limite pela direita é:
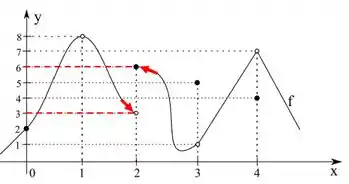
Pela definição que mostrei lá no passo 1, vemos que os laterais não batem. Então, o limite não existe.
Não existe
Passo 5
Vamos para o ponto . Vemos pelo gráfico que:
Assim,
Passo 6
Por último (ufa!), o ponto . Vemos pelo gráfico que:
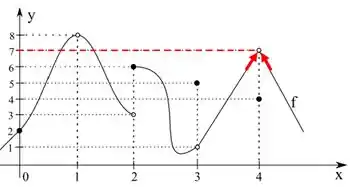
Assim,
Resposta
Não existe
Exercício Resolvido #3
Esboce o gráfico da função a seguir e use-o para determinar os valores de para os quais
existe:
Passo 1
Faaaala ai! Bora pra mais uma questão de limites laterais?
Beleza, vamos analisar nossa função, ela é uma função dada por partes, e são 3 intervalos diferentes onde ela está definida.
Vamos fazer o seguinte, primeiro desenhar esse negócio aí. Temos 3 funções então vamos dividir em 3 partes
- Temos a função de primeiro grau quando então o gráfico antes de igual a vai ser essa reta.
- Na parte onde está entre e ele vai ser a reta .
- E quando vamos ter a parte da parábola , o gráfico vai ficar então
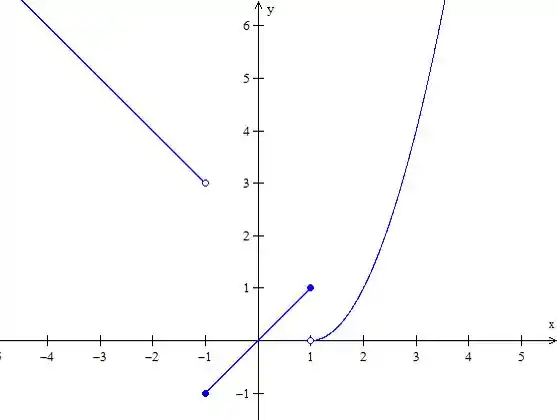
Passo 2
Então, já que a estrutura está montada, vamos olhar no gráfico os pontos onde
existe, ou seja, onde vale:
Passo 3
Cara, conseguimos ver que esses limites existirão para todosem que a função não muda sua lei de formação.
Resumindo, para que o limite lateral seja igual, os pontos teriam que seguir o mesmo padrão dos dois lados ou ter o limite entre os pontos onde trocam-se os regimes de função dando a mesma coisa.
Pelo gráfico, a gente pode ver que tem dois pontos em que a função não segue esse padrão de contínua, que são os pontos e
Então vambora dar uma olhada nos limites laterais desses ’s
Passo 4
Pelo desenho, vemos que:
- Para
Temos dois limites laterais, que são valores a direita de , ou seja um número um pouquiiiiinho maior que , vamos usar então nossa função do meio, a e fazer o limite dela
Para o limite temos valores a esquerda de , ou seja, um numero um pouquiiinho menor que , vamos usar então nossa primeira função, a e fazer o limite dela
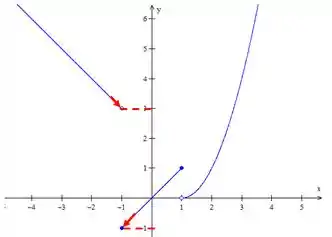
Olha só, os limites laterais deram diferentes, então nosso limite no ponto não existe
Passo 5
Para
Temos dois limites laterais, que são valores a direita de , ou seja um numero um pouquiiiiinho maior que , vamos usar então nossa função de baixo, a e fazer o limite dela
Para o limite temos valores a esquerda de , ou seja, um numero um pouquiiinho menor que , vamos usar então nossa função do meio, a e fazer o limite dela
Então no ponto também temos limites laterais diferentes, logo o limite também não existe nesse ponto
Então pode assumir qualquer valor, menos e , logo temos
Resposta
Exercício Resolvido #4
a) Do gráfico de , explique os pontos em que é descontínua e explique por quê.
b) Para cada um dos pontos indicados na parte (a), determine se é contínua à direita, à esquerda ou nenhum deles.
Passo 1
Vamos que vamos
A questão cobra de forma visual o conceito de continuidade.
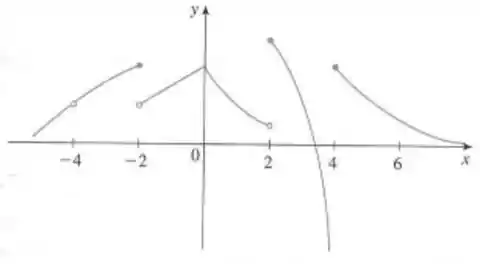
O enunciado nos dá o gráfico de uma função e pede, no item (a), para procurarmos os pontos em que não é contínua.
No item (b) é pedido para verificar se existem pontos de continuidade lateral.
É importante lembrar que uma função é contínua lateralmente em um ponto se um dos limites laterais de for igual ao valor da função naquele ponto.
Passo 2
Uma função contínua não tem buracos ou saltos.
Notemos que a função tem um buraco em e saltos em , e . Assim, não é contínua nesses pontos.
Então temos que não é continua em
Show! Matamos a letra
Passo 3
Agora vamos analisar esses pontos
Como é um ponto em que o gráfico de tem um buraco, a função não é contínua nem à direita nem à esquerda neste ponto.
Passo 4
Em , é contínua à esquerda pois o limite lateral à esquerda é igual ao valor da função, isto é,
Passo 5
Em , é contínua à direita pois o limite lateral à direita é igual ao valor da função, isto é,
Passo 6
O mesmo ocorre em . Em , é contínua à direita pois o limite lateral à direita é igual ao valor da função, isto é,
Resposta
a) , , e .
b) Contínua à direita: e .
Contínua à esquerda: .
Nenhuma delas: .
Exercício Resolvido #5
Resolva o seguinte limite:
Passo 1
Já entrou uma secante aqui no meio, ai ai ai ai... Mas relaxa que, antes de tudo, vamos lembrar o que é . A secante é basicamente dada por:
Tá, mas e esse ai? Aqui a gente vai usar o circulo trigonométrico, que tem a seguinte carinha:
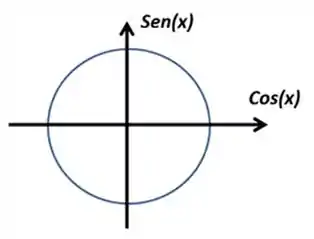
O círculo trigonométrico é basicamente um círculo de raio , e a partir dele vamos ter diferentes valores para as funções de ou dependendo do valor de beleza?
Aqui tem alguns principais valores de nos quais começamos marcando em 0 e vamos somando no senido anti-horário. Esses, são os valores de quando eles cruzam os eixos do seno e do cosseno. Vamos ficar com isso em mente!
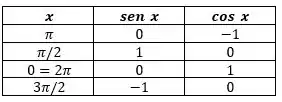
Passo 2
Agora voltando para o enunciado da questão, queremos encontrar:
Uma informação importante a ser dita, é que cada volta no círculo trigonométrico representa . Então alguns valores de apesar de serem diferentes vão representar a mesma coisa, pois damos voltas sobre os mesmo valores, como é o caso do quando adicionamos . Saca só:
Assim, o valor do seno e do cosseno de vai ser o mesmo que o de
Então, vamos substituir o na equação, ficando com:
Beleza, a gente já tem noção que isso vai dar . Resta saber como estamos nos aproximando de .
Passo 3
Pensando nessa análise do sinal, você percebe que a aproximação é feita pela esquerda, ou seja, para valores menores que .
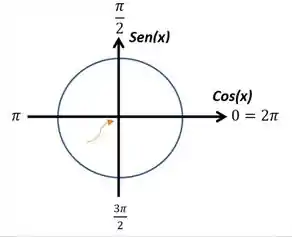
Bom, podemos ver que, quando está vindo por trás de , temos valores de cosseno negativo, pois ele está no eixo negativo do Dessa forma, podemos dizer que a aproximação se dará para . Portanto,
Resposta
Exercício Resolvido #6
Calcule o limite ou prove que não existe:
Passo 1
Opa, fala ai, tudo bem??
Já batemos de cara com um módulo, e ficamos como? Com receio já da questão né? Nããão! Haha cola comigo que vai ficar mais de boinhas de entender o que a gente faz 😉
Vamos analisar primeiro a função de dentro. Abrindo o módulo ficaria assim:
Para números a parte de dentro do nosso módulo daria negativo né? Entao vamos dizer que:
- Para temos essa função aqui porque o sinal vai mudar já que temos um módulo de alguma coisa negativa, tranquilinho?
- Para temos essa função aqui porque o sinal vai se manter já que temos um a parte de dentro é positiva, tranquilinho?
Então, juntando essas duas informações podemos reescrever nosso módulo da seguinte forma:
Maaaas calma ai, nossa função é
Por isso, vamos precisar dividir essas duas partes da função por , então ficamos com
Mas a gente pode simplificar esse já que ele esta no numerador e no denominador!
O que nos dá:
Bem mais tranquilinho, né? E olha que não foi mágica rsrs.
Passo 2
Como queremos o valor em e a função muda sua lei nesse ponto, devemos analisar os limites laterais.
Se forem iguais teremos o resultado do limite. Caso não, saberemos que o limite não existe:
Temos dois limites, o limite lateral esquerdo que são valores um pouquinho menor que que é assim:
Só que a gente já viu como simplificar essa função, para valores menores que temos
Como não temos nenhum aí, ela continua a mesma, então nosso limite lateral esquerdo dá
Agora para o limite lateral direito, temos valores um pouquinho maior que , então vamos usar a função de baixo!
Mas vimos que podemos simplificar assim
Então nosso limite lateral direito ficou
Oxi, um deu e o outro , e aí?
Isso quer dizer que os limites não batem. Concluímos que não existe!
Viu, não precisa ficar com medo de módulos 😊!
Resposta
Exercício Resolvido #7
Dadas as duas funções abaixo:
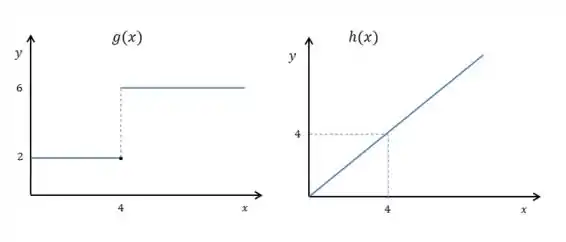
Calcule os limites laterais dados abaixo e verifique se o limite existe, comparando os limites laterais:
, , onde:
Passo 1
Opaaa, fala ai! Vamos continuar com nossos exercícios!
Bom, vamos primeiro escrever as leis das funções. Vamos começar por
A função é uma função com equação:
Já que:
Quando ,
Já a função é uma função constante dada por partes, descrita por:
Já que temos a reta quando e a reta quando
Passo 2
Show agora que já vimos bem quem são essas funções, vamos calcular os limites laterais delas!
Vamos calcular primeiro os limites laterais de por serem mais tranquilos:
Como essa função não tem probleminha, temos que os limites laterais são iguais, e é só substituir o valor!
Beleza, como você pode ver, eles são iguais.
Já a função vai precisar de uma atenção maior, a gente separou elas em duas partes né, para valores maiores que e para valores menores ou iguais a
Como o nosso limite lateral direito são valores um pouquinho maiores que , vamos usar a função , então temos que:
E, para o limite lateral esquerdo, temos valores um pouquinho menores que , então vamos usar a função , então o limite fica
Passo 3
Belezinha, agora que achamos os limites vamos relembrar uma coisinha.
Ele diz que
E, como ele quer os limites laterais de vamos fazer isso aqui:
E, para o limite esquerdo temos
Maaas em limites a gente tem uma propriedade que é: O limite do produto é igual o produto do limite. Então podemos usar os limites que acabamos de calcular. E fica exatamente assim:
Passo 4
Usamos ali a propriedade do limite de um produto. Agora é só a gente pegar os valores que calculamos:
E já achamos esses limites
Então temos que
Show! Matamos o limite da direita de
Passo 5
Agora vamos partir para o limite esquerdo!! Fazendo a mesma cois
E já achamos esses limites
Então temos que
Passo 6
Vimos então que os limites de são
Esses limites são diferentes, então dizemos que o limite não existe em
Resposta
E o limite não existe.
Exercício Resolvido #8
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Faaaala aii! Bora continuar nosso estudo pra ficar fera em limites!
Bora começar lembrando o que é uma função contínua!
Uma função é contínua em um ponto se ela estiver definida nesse ponto e, além disso, o valor da função neste ponto coincidir com o valor do limite. Assim, devemos calcular tanto o limite como o valor da função em e compará-los.
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a . Então, a expressão que devemos usar para o limite é .
Note que temos uma indeterminação do tipo . Ixi e agora?
Para eliminá-la, vamos fatorar o numerador e o denominador.
Para podemos colocar em evidencia, e ficamos com
Para temos uma diferença de quadrados
Que é
Que podemos escrever assim:
Passo 2
Reescrevendo nosso limite, temos:
Podemos simplificar o fator de modo que o limite fica
Shoow agora sumiu nossa indeterminação, podemos substituir!
Assim, encontramos nosso limite.
Agora temos que lembrar que , sendo assim a fução não é contínua em .
Passo 3
O esboço do gráfico da função é:
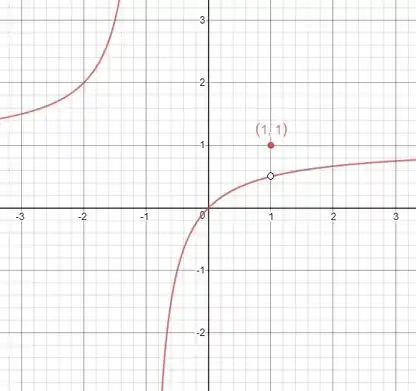
Resposta
A fução não é contínua em . E seu gráfico é:
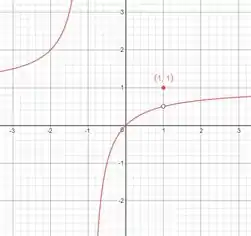
Exercício Resolvido #9
Explique por que a função é descontínua no dado número . Esboce o gráfico da função.
Passo 1
Opaa, e ai!!!
O enunciado fornece uma função e um ponto e pede para justificarmos o motivo de não ser contínua nesse ponto.
Uma função é contínua em um ponto se ela estiver definida nesse ponto e, além disso, o valor da função neste ponto coincidir com o valor do limite. É isso que temos que verificar.
Passo 2
Para , a expressão da função é , que só não poderia ser utilizada exatamente em .
Assim, é bem definida em todos os pontos já que em ela é definida a parte a vale , de acordo com a nossa condição de baixo!
Então o domínio de é a reta real toda.
Passo 3
Show, mas ela ser definida não quer dizer que todos os nossos problemas estão resolvidos haha.
Vamos calcular o limite de quando tende a . Quando tomamos o limite, nos aproximamos de por valores de próximos de porém nunca iguais a .
Então, a expressão que devemos usar para o limite é , porque estamos usando números beeeem próximos de mas, ainda sim , que é a condição para usar essa expressão!
Passo 4
Vamos calcular os limites laterais.
O limite à esquerda é
O limite à direita é:
Os limites laterais são diferentes (logo o limite não existe) e diferem também do valor da função em ().
Por isso, não é contínua em .
Passo 5
O esboço do gráfico da função é:
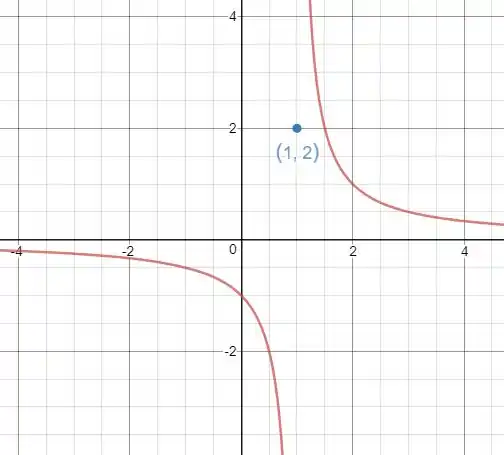
Resposta
Os limites laterais são diferentes (logo o limite não existe) e diferem também do valor da função em ().
Por isso, não é contínua em .
Exercício Resolvido #10
Calcule os limites laterais de em , se .
Passo 1
Fala aii. Nossa função é uma função composta, pois depende de outra função, que é a . Já a função , por sua vez, é uma função dada por partes, pois dependendo do valor de ela assumirá uma forma diferente. Para valores de ela será , e se usaremos .
O que o enunciado nós pediu foi pra calcular os limites laterais quando . Então vamos começar escrevendo como fica a definição de de acordo com a :
Agora, vamos calcular os limites laterais que ele pediu fazendo as respectivas substituições e analisando os sinais.
Passo 2
Mas fica ligado numa coisa: quando , ou seja, , usaremos a primeira expressão para . Quando , ou seja, , usaremos a segunda expressão para beleza?
Show! Então no primeiro limite:
Da mesma forma que o primeiro, vamos substituir esse segundo limite lateral:
Substituições feitas! Agora só precisamos fazer a análise dos sinais.
Passo 3
Vamos começar no primeiro limite. Nesse caso, vou trazer o círculo trigonométrico para pensarmos sobre o sinal desse “infinito”, se é positivo ou negativo:
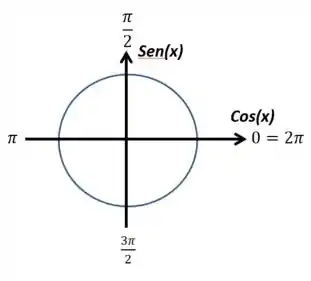
Repara que, para valores logo acima de (valores um pouquinho maiores que ), o seno é positivo, pois ficará na parte positiva do eixo do seno. Com isso:
Portanto,
Aqui nós não vamos escrever o no final porque ele vai ser um número muuuito pequeno quando comparado ao então podemos simplesmente desprezar. A única coisa que vai fazer diferença mesmo é o sinal.
Passo 4
Olhando para o mesmo desenho de antes, vamos reparar que o seno é negativo para valores logo antes de (valores pouco menores que ). Logo,
Portanto,
Repara que aqui também desprezamos o por ele ser desprezível ao comparado com o infinito.
Com isso encontramos nossos dois limites laterias.