Introdução e Propriedades dos Limites
Teoria
Fala aí. Seja Bem Vindo(a) aos estudos sobre Limites, vem com a gente que vamos te mostrar tudo que você precisa saber tim tim por tim tim.
E pra gente começar, me responda uma coisa: Você saberia dizer de qual valor a função se aproxima quando fazemos o ficar bem pertinho do número ?

Bom, essa é a pergunta “chave” do estudo dos limites. Ao calcularmos um limite, o que queremos saber é de que valor uma função se aproxima quando fazemos o se aproximar cada vez mais de um determinado valor.
Nós representamos essa pergunta matematicamente através da expressão:
Como nossa função é , escrevemos:
E lemos da seguinte forma: Qual o limite de quando tende a 2? Essa setinha embaixo do é que quer dizer que o tende a .
Mas o que é tender a ? Isso significa que os valores de ficam muito próximos de , sem ser exatamente .
Para entender melhor, vamos pegar alguns valores que se aproximam de e vamos calcular a função pra ver o que acontece:
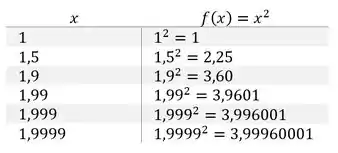
O que podemos ver é que quanto mais perto do o fica, mais perto de a função também ficará. Mas perceba que o ainda não é , e a também não é . Mas eles se aproximam cada vez mais desses valores.
Isso também pode ser mostrado no gráfico que vimos mais acima:

Onde as setas vermelhas indicam a aproximação do e as azuis representam a aproximação da função. Assim, também podemos dizer que o limite de quando tende a é igual a .
Bom, nós teríamos chegado a essa resposta substituindo diretamente o por na função, dessa forma:
Nós tiramos o , trocamos o por dois na função e calculamos normalmente:
E teremos exatamente o mesmo valor. Mas infelizmente isso nem sempre é verdade, e mais à frente em nossos estudos aprenderemos a lidar com situações onde não poderemos fazer isso.
O legal é que em boa parte dos limites que iremos calcular, nós poderemos fazer essa substituição diretamente. Então essa é a primeira coisa que iremos tentar fazer para calcular um limite. E faremos isso sempre, em TODAS as questões de limite.
EXEMPLOS:
Lemos: o limite de quando tende a zero. E resolvemos substituindo diretamente o por zero na função:
Assim, dizemos que o limite de quando tende a zero é igual a zero!
Lemos: o limite de quando tende a . E resolvemos substituindo diretamente o por na função:
Esse é o número de Euler, um valor constante de aproximadamente , então podemos deixar nossa resposta em função dele mesmo. Assim, dizemos que o limite de quando tende a é igual a
Lemos: o limite de quando tende a . E resolvemos substituindo diretamente o por na função:
Aqui vamos lembrar que o equivale a . Então, o que estamos procurando é o que é igual a .
Assim, dizemos que o limite de quando tende a é igual a .
E pra ficar craque mesmo nos limites, é bom fazer bastante exercício!
Propriedades Básicas do Limite.
As propriedades estão aqui pra ajudar a gente a saber o que podemos fazer na hora de calcular um limite. Nós faremos muito o uso delas, o que vai facilitar bastante a nossa vida.
Vamos ver algumas:
- O que acontece com o limite de uma função constante?
- O que acontece com o limite de uma função qualquer que é multiplicada por uma constante?
- E se tivermos uma soma ou subtração de funções?
- E para a multiplicação também poderemos fazer isso, veja:
- Assim como nos produtos de funções, quando tivermos um quociente entre funções, também poderemos calcular o limite separadamente:
- Quando tivermos uma função composta contínua, poderemos colocar o limite pra dentro da função.
Pensa comigo, se a função é constante, ela sempre terá o mesmo valor. Por exemplo:
Se a função é sempre igual a , não importa para que valor o está indo. Nem tem na função pra mudar alguma coisa. Então, esse limite permanece sendo igual a , que é onde a função sempre vai estar.
Isso vai acontecer para todas as funções que foram constantes.
Então, essa é nossa primeira propriedade:
O limite de uma função constante é sempre a própria função constante
Vamos fazer
Vimos que podemos substituir diretamente o por para calcular o limite. Assim:
Mas você concorda que daria no mesmo se nós tivéssemos aplicado o limite apenas ao e depois multiplicado por ? Veja:
Viu, exatamente a mesma coisa! Vemos que essa também é uma propriedade dos limites:
Quando queremos calcular o limite de uma função que está multiplicada por uma constante, podemos colocar a constante para fora do limite, calcular o limite da função e depois multiplicar a constante.
Nesse caso, podemos dividir esse limite em limites menores, aplicando o limite a cada termo da função. Assim:
Então fazemos o limite de cada um:
Isso foi possível por conta da propriedade de soma/diferença:
O limite da soma/diferença de duas funções e é igual ao limite de mais/menos o limite de
Aplicamos o limite a cada função e depois multiplicamos tudo:
Essa propriedade diz que:
O limite do produto de duas funções e é igual ao limite de multiplicado pelo limite de .
O limite do quociente de duas funções e é igual ao limite de dividido pelo limite de , desde que o denominador não seja 0.
Dentro dos tipos diferentes de funções que podemos ter, existe uma categoria chamada de funções contínuas. E para elas existe uma propriedade todas especial. Apenas para contínua, teremos:
Mas o que são funções contínuas? Relaxe, teremos um capítulo inteiro só para falar sobre elas. Por enquanto, vamos mostrar algumas funções que sempre são contínuas e você poderá aplicar essa propriedade tranquilamente:
- Raízes:
A função é uma função composta, pois temos uma função dentro de uma outra função que é a raiz quadrada. Ela é uma função contínua, então podemos jogar o limite para dentro dela:
Calculamos esse limite e ao final aplicamos a raiz:
- Exponenciais:
- Funções trigonométricas:
- Funções logarítmicas:
Funções exponenciais também são funções contínuas, e podemos fazer a mesma coisa, jogando o limite para o expoente:
O mesmo acontecerá com funções trigonométricas do tipo seno e cosseno, poderemos passar o limite para dentro delas, e aplicá-lo ao argumento:
As funções logarítmicas também são contínuas e permitem a aplicação dessa regra tranquilamente:
Indeterminações
Como você pode ter percebido, são muitos os casos onde poderemos fazer a substituição direta do para calcular um limite, mas precisamos ficar atentos a um detalhe muito importante. A matemática precisa ser respeitada sempre, e existem algumas operações que não poderemos resolver. São as chamada indeterminações.
Mas, o que são essas indeterminações?
Imagina que queremos calcular o seguinte limite:
Se substituímos por :
Opa!!! Mas quanto dá ?
Não temos a resposta para essa pergunta porque ela não existe.
Essa expressão é indeterminação. Existem vários tipos de indeterminações, dentre as quais as mais comuns são:
Quando caímos em expressões deste tipo, não podemos continuar, pois não há resposta para elas. Não se preocupe que vamos ver como sair das indeterminações com mais calma depois. Mas é muito importante já alertarmos a você que nem sempre poderemos calcular os limites dessa maneira. Então fiquem atentos às indeterminações, caso elas apareçam.
Eu sei que parece muita informação, mas iremos usar tanto essas propriedades que ficará natural com o tempo. Então, VAMOS PARA OS EXERCÍCIOS AGORA!
Propriedades Básicas do Limite.
Indeterminações
Exercícios Resolvidos
Exercício Resolvido #1
Determine o seguinte limite:
Passo 1
Fala aiiii, tudo bem? Estamos começando agora nosso estudo de limites e pode ser que seja uma matéria completamente nova pra você, mas fica tranquilo que vamos começar formando uma base bem legal pra você entender tudinho e nunca mais ter problemas com essa matéria.

Bom, antes de resolvermos a nossa questão, vamos tentar interpretar o que o enunciado está dizendo. Ok? O problema diz pra calcular:
O que esse limite está querendo saber é: De que valor a função ) se aproxima quando fazemos se ficar cada vez mais perto do 2. Ou seja, dizemos que o tende a 2, e é isso que significa aquele embaixo do limite.
Passo 2
Você não precisa desenhar essa função pra calcular o limite, mas deixa eu te mostrar uma coisa que pode clarear nossas ideias. Vamos ver o gráfico dela:
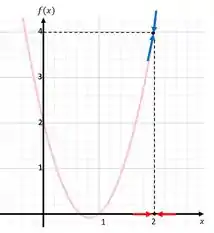
Repare que quando a gente olha para o eixo e vai se aproximando do , que está indicado pela setas vermelhas, a nossa função vai também se aproximando de uma valor , indicado pelas setas azuis.
Pois bem, é isso que o limite que saber da gente. Para que valor caminha a nossa função quando a gente aproxima o valor de a um número de nosso interesse. Dizemos, no nosso caso que o limite da função é igual a quando o .
Mas a gente viu isso pelo gráfico, e não é sempre que dá pra desenhar o gráfico das funções, certo. Então, agora que a gente já sabe o que significa esse limite, vamos ver como resolver de um jeitinho mais direto.
Passo 3
Para resolver esse limite, o que nós fazermos primeiramente é observar que a função é composta por três termos, que são essas parcelinhas ali, o , o e o .
Quando isso acontecer, nós poderemos usar uma propriedade dos limites que diz que a gente pode calcular os limites de cada termo separadamente e depois juntar todo mundo. Ou seja, vamos transformar nosso limite em:
Outra coisa que a gente também pode fazer é usar outra propriedade que diz que quando houver uma constante (um número) multiplicando a função, nós podemos colocá-la pra fora do limite, multiplicando na frente dele. Com isso, podemos tirar o no primeiro limite, e o no segundo. E vai ficar assim:
No último a gente não mexeu, porque só tem o lá. Vamos olhar pra ele com calma logo mais.
Passo 4
Agora que já está tudo arrumado, chegou a hora de calcularmos de fato os nossos limites. E nós faremos isso, substituindo o valor de por em cada um do termos. Isso mesmo, substituindo. Vamos lá:
Nós tiramos o operador e trocamos o por em cada termo, ficando com:
Reparou que no último não tinha o pra substituir. Nesse caso, fica o próprio valor mesmo que já estava lá.
Agora é só resolver essa expressão e ver o que encontramos. Lembrando de fazer primeiro as potências, depois as multiplicações e só por último as somas e subtrações.
E assim, chegamos no nosso resultado. Idêntico ao que vimos no gráfico.
Obs. O que fizemos no final das contas, foi só substituir o por na função que ele deu e encontrar o resultado dela. Aí você se pergunta: Então, por que demos essa volta ao mundo?
Bom, nem sempre o valor que a gente obtém quando faz essa substituição direta é uma valor válido. Por isso precisamos sempre começar tentado substituir pra conferir se dá certo. Caso a gente não consiga resolver dessa forma, procuramos outros meios de resolução. Mas sempre vamos começar tentando substituir, ok? 😊
Resposta
Exercício Resolvido #2
Determine o limite abaixo:
Passo 1
Ficou assim, né?

Calma que devagarinho a gente chega lá! Uma coisa que pode estar incomodando a gente é que temos uma fração e ainda tem esse diferentão ali no meio de tudo. Mas vamos olhar mais de perto o que precisamos.
Esse é apenas um valor constante, a mesma ideia do . Então, ele será tratado como um número, ok.
O que temos que fazer é calcular o seguinte limite:
E quem vai ajudar a gente nisso são as propriedades dos limites.
Passo 2
A primeira coisa que podemos observar é que a função que queremos calcular o limite, é uma razão. Então, podermos usar uma propriedade dos limites que diz que quando temos o limite de uma razão, esse limite pode ser aplicado no numerador e no denominador separadamente e depois a gente junta os resultados.
Então o que era:
Se transforma em:
Agora vamos olhar para o numerador e para do denominador separadamente.
Passo 3
- No numerador temos:
- No denominador temos:
Como existem dois termos ali, podemos separar esse limite em duas parcelas usando a propriedade da soma de limites. “O limite da soma é a soma dos limites”.
Assim ficaremos com:
Além disso, podemos tirar o que é uma constante de dentro do primeiro limite e passar ele para frente multiplicando.
Que também podemos separar nos limites de cada termo, ficando com:
Agora que já arrumamos tudo, vamos resolver de fato o limite.
Passo 4
Nos mexemos no nosso limite e ele passou de:
Para:
Agora o que vamos fazer é aplicar o limite, e pra isso vamos substituir o por em cada um dos limites. Nós tiramos o operador e trocamos todos os valores de por .
Fazendo isso, teremos:
Agora é só resolver a expressão que encontramos.
Passo 5
Resolvendo a expressão, lembrando de calcular primeiro as potências, depois as multiplicações, em seguida as somas e subtrações e só por último a divisão indicada na fração.
Ahh, detalhe importante: Todo número elevado a zero é igual a . Lembra que falamos que esse era só um número? Assim , bem como
Como isso:
Aqui temos uma divisão de sinais contrários. O que vai dar pra gente sinal negativo. Assim:
Fim! 😊
Obs. Poderíamos ter substituído o valor de diretamente na função inicial. Mas nosso foco aqui é entender as propriedades que podem ser aplicadas aos limites, ok.
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule o limite abaixo
Passo 1
FALA AÍÍÍ!! Se você reparar, não podemos substituir na equação. Se substituirmos, o denominador seria zero ahaha. Assim, para calcular esse limite podemos fatorar o numerador e o denominador pra facilitar nossa vida!

Passo 2
Vamos primeiro fatorar o numerador . Para encontrarmos as raízes da equação
Utilizaremos a fórmula de Bhaskara
Beleza?!
Primeira coisa que precisamos fazer é identificar quem é o , e . Lembra da carinha da nossa equação do 2º grau? Ela tem essa carinha aqui
Então, comparando com a nossa equação
Conseguimos encontrar os valores de , e :
Beleza?! Agora vamos utilizar esses valores para encontrar o :
Substituindo os valores , e , temos
Fazendo as continhas, temos
Agora podemos substituir o valor de e os demais valores na fórmula de Bhaskara:
Teremos então duas raízes:
E
Portanto, as raízes da equação são e ! Assim, a nossa equação fatorada será
Beleza?!

Passo 3
Agora vamos escrever o limite que temos no enunciado só que com a fatoração que achamos
OPAAAAA! Se você reparar podemos simplificar os termos que temos no numerador e no denominador
Ou seja,
Beleza?!
Resposta
Exercício Resolvido #4
Elaboração Própria
Utilize as propriedades de limite para resolver a questão abaixo
Passo 1
FALA AÍÍÍ!! Para resolver essa questão precisamos utilizar as propriedades de limites, certo?! Então vamos lááá!!

Podemos começar aplicando a propriedade do limite da diferença! Afinal, temos dentro do limite a diferença entre dois termos, rs! Essa propriedade nos diz que o limite da diferença é igual a diferença dos limites! Ou seja,
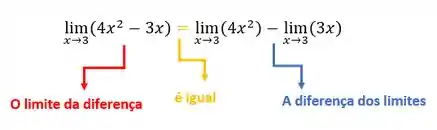
Beleza?!
Passo 2
Agora podemos aplicar a propriedade do limite do produto, pois se você reparar temos o multiplicando o e o multiplicando o . Tá... mas o que diz essa propriedade?

A propriedade do limite do produto diz que o limite do produto é igual ao produto dos limites. Vamos olhar primeiro para o
Assim,
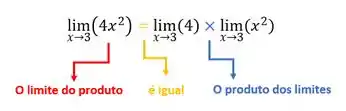
Show de bola?!
Passo 3
Vamos seguir o mesmo raciocínio para a outra parcela
Assim,
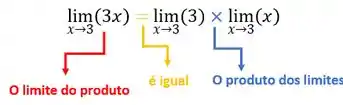
Beleza?!
Agora vamos juntar tudo! Vamos ficar com
Por fim, aplicaremos o limite em cada parcela
E assim temos a nossa resposta
Show de bola?!
Resposta
Exercício Resolvido #5
Determine a soma dos limites indicados abaixo:
Passo 1
Oiee, olha nós aqui novamente! E vamos partir pra mais uma questão “filé” de limites.
Bom, a questão pede pra gente resolver essa soma de limites.
E a primeira coisa que temos que ter atenção é que cada limite tende pra um valor diferente. Então, não podemos misturar as coisa, ok?
Ahhh, mas tem esse esquisitos ali! Fica tranquilo que esse é o logaritmo, e ele não vai ser um problema pra gente. já já a gente fala sobre ele. Vamos primeiro ver o que podemos fazer para aplicar o limite em cada parcela. 😉
Passo 2
Há uma propriedade dos limites específica pra quando vamos calcular o limite de um logaritmo. Ela nos diz que podemos levar o limite pra dentro do logaritmo e aplicá-lo a função que estiver lá dentro, e depois calculamos o logaritmo do resultado. Assim, nosso limite que era:
Se torna:
Passo 3
Agora podemos aplicar o limite em cada caso. Para isso nós tiramos o operador do primeiro e substituímos o por , e tiramos também o operador do segundo e substituímos o por . Ficando com:
Beleza, o limite já foi, agora o que nos resta é resolver essa expressão aí. Faremos isso no próximo passo.
Passo 4
Para resolver a expressão, começamos com as continhas que estão dentro dos logaritmos.
Beleza. Agora é hora de calcularmos os ’s.
Mas o que é o logaritmo? Na verdade, o logaritmo é o valor do expoente que devemos colocar numa base (que é esse valor pequenininho que fica embaixo do )pra que
resulte no número que teremos dentro dos parênteses. Veja no esquema:
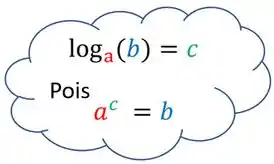
Logo, o que queremos saber é quem deve ocupar o lugar desse verdinho aí.
Ou seja:
O está perguntando pra gente, qual é o valor que devemos elevar o para encontrar como resultado o . E a resposta é , porque .
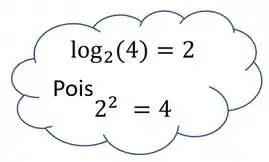
E o está perguntando pra gente, qual é o valor que devemos elevar o para encontrar como resultado o . E a resposta é , porque .
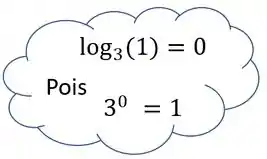
Com isso, temos:
Viu como entendendo o que a questão queria direitinho a gente conseguiu resolver?
E esse é o nosso resultado! 😁
Resposta
Exercício Resolvido #6
Avalie o seguinte limite:
Passo 1
Fala aiiii, tudo na paz? Bom, antes de resolvermos a nossa questão, vamos tentar interpretar o que está acontecendo ali. Ok?
O que esse limite está querendo saber é: De que valor a função se aproxima quando fazemos se ficar cada vez mais perto do 1. Ou seja, dizemos que o tende a 1 .
Agora dá aquela reparada na função:
Olhando bem pra carinha dela vemos que podemos separá-la em dois pedaços, e para resolvermos usando as propriedades dos limites vamos olhar pedacinho por pedacinho.
Podemos olha pra ela como sendo dois blocos que estão sendo multiplicados. Sendo:
e
Como é uma multiplicação desses dois carinhas aí, nós vamos precisar usar a propriedade do limite de um produto. Onde nós podemos aplicar o limite em cada um dos dois blocos (mas sem ser o de carnaval rs), saca só:
Aqui vai ser o nosso BLOCO 1 e o BLOCO 2. Agora vamos resolver esses blocos!
Passo 2
Analisando primeiro o BLOCO 1, nós vemos que temos uma constante multiplicando o então podemos jogar ela para fora do limite da seguinte forma:
Agora, vamos resolver esse limite fazendo a substituição direta do por , já que no nosso limite:
Show! BLOCO 1 foi, vamos deixar esse resultado guardadinho aqui. Agora partiu BLOCO 2.
Passo 3
No BLOCO 2 nós temos um número de Euler querendo dificultar a nossa vida, mas não vamos nos abalar! É só a gente não mexer com ele que ele não implica com a gente rsrsr. O que nos interessa é esse que está na dentro da raíz no expoente dele.
Como a função é contínua, nós podemos jogar o limite direto lá na raiz e ficamos com o seguinte:
Então nosso real problema é na verdade resolver só:
Tá, mas e agora, o que faço com aquele chatão? Nada! Você simplesmente substitui o limite na raiz e fica com:
Fim do BLOCO 2, agora vamos buscar aquele resultado do BLOCO 1 e juntar tudo?
Passo 4
Lembra que nossos BLOCOS estavam sendo multiplicados? O que nós tinhámos:
E agora encaixando o resultado de cada BLOCO no seu devido lugar ficamos com:
Feshow! 😊
Resposta
Exercício Resolvido #7
Suponha e . Determine:
Passo 1
Oi oi oiee, turubom? Nessa questão nós temos três limites de funções diferentes já com seus respectivos valores calculados. O que ela quer em cada item é que a gente calcule o novos limites para algumas operações que podem ser feitas com essas funções.

Calma que quem vai ajudar a gente nessa são as propriedades dos limites.
Repara que em todos esses limites vamos poder usar a mesma propriedade, pois tanto limite da soma, da multiplicação ou da divisão podem ser separados. Então vamos usar as propriedades e substituir os valores dados (uhuul \o/). Se liga como vai ser isso!
Passo 2
Nesse primeiro limite temos a soma das funções. Então, podemos aplicar o limite em cada parcela, tipo assim:
Cada limite separado que achamos aí é exatamente o que o problema deu pra gente. Olha que coisa boa!
Substituindo o valor de cada um teremos:
Ou seja,
Passo 3
Nesse segundo limite temos uma multiplicação de funções. Onde, também podemos colocar o limite em cada pedacinho dela. Usando as propriedades para separar em blocos ficamos com:
Novamente temos exatamente esses limites no enunciado, e substituindo os valores agora:
Ou seja,
É uma sensação boa quando você encontra uma multiplicação com né? Eu amo!
Passo 4
Nesse nosso último item temos a soma e divisão de funções. Sei que ela tá meio feinha, mas também podemos separar em bloco. Vamos começar separando a soma:
Repara que agora temos dois blocos que ainda precisamos destrinchar mais um pouco. Começando com o primeiro que tem uma constante sendo multiplicada pela função:
Substituindo o valor:
Passo 5
Agora analisando o nosso segundo bloco da letra (c) temos,
Repara que aqui também temos a multiplicação com uma constante, então:
Substituindo os valores de cada limite teremos:
Olha o ai de novo
Passo 6
Por fim, vamos juntar os blocos para voltar ao enunciado original, beleza? Ou seja,
Substituindo os valores:
Fim! 😊
Resposta
Exercício Resolvido #8
Se , determine:
Passo 1
- Olá! Tudo bem? Bora ver mais essa?
- Vamos tentar chegar no limite do enunciado aqui de novo. Perceba que a gente pode fazer o seguinte:
Aqui, a ideia é aplicar a propriedade dos limites. Se fizermos aparecer aquele limite que nos foi dado no enunciado poderemos substituí-lo por , certo? Dessa forma, vou forçar o limite do enunciado a aparecer, multiplicando em cima e embaixo por :
Aqui agora a gente vai poder separar em dois limites, utilizando a propriedade do produto de limites:
Beleza até aqui? Vamos continuar...
Passo 2
Do enunciado, a gente tem que . Então a gente vai substituir isso ali no nosso produto!
E aí nesse outro limite é só a gente substituir o por :
Beleza! Esse já foi😉
Passo 3
E aí a gente pode separar assim:
Passo 2
Olha o limite do eunciado ali! A gente sabe que:
Então a gente substituir isso no nosso produto, assim:
E aí nesse outro limite a gente pode substituir o por e fica:
E acabamos por aqui! 😁
Resposta
Exercício Resolvido #9
Calcule o limite:
Passo 1
Fala aí, vamos continuar nossa caminhada pelas propriedades dos limites, e esse exercício aqui vai ajudar a gente em outra aplicação bem legal dessas propriedades.
O que o enunciado pede pra gente é pra determinar pra que valor a função se aproximará quando nós fizermos o tender a .
Pra entendermos bem o que faremos, vamos olhar com calma para o limite.
Veja, que a função que está ali é uma fração, e essa fração ainda está elevada ao quadrado. Calma que não vamos precisar resolver essa potência “de cara” ainda não.
Para resolver esse limite faremos uso de algumas propriedades que vão deixar tudo bem mais simples. Vamos ver a primeira no próximo passo.
Passo 2
Bom, a primeira propriedade que iremos usar, diz pra gente que quando temos uma função elevada ao um expoente (como é o caso da nossa que está ao quadrado) nós podemos passa o limite pra dentro dela, calcular o limite do que está dentro, e só depois resolver a potência.
Vai ficar assim, ó:
Assim, essa potência chata aí não será mais um problema pra gente.
Passo 3
Agora vamos olhar o que ficou dentro da potência. Ficamos com o limite de pra resolver, e como é uma fração, podemos calcular o limite do numerador e do denominador separadamente, e essa é mais uma propriedade dos limites que podemos usar aqui. Assim, ficamos com:
Show, ainda dá para melhorar um pouco mais.
Passo 4
Agora repara que em cada um desses limites que sobraram, temos funções polinomiais com vários termos. Uma outra propriedade dos limites diz pra gente que podemos calcular o limite de cada termo separadamente e depois juntarmos tudo. Além disso, ainda podemos colocar o que for constante pra fora do limite multiplicando na frente dele. Com isso transformamos nosso limite em:
Maravilha, agora chegou a hora de resolver de fato o nosso limite!
Passo 5
Perceba que o que fizemos foi transformar nosso limites que era:
Em
E assim poderemos aplicar o limite em cada pedacinho separadamente. Pra isso a gente retira o operado e substitui o valor de por dois em todos os lugares que aparecer o . Aí ficaremos com:
Com isso, só nos resta resolver essa expressão que sobrou. Lembrando sempre de resolver primeiro as potências de dentro, depois as multiplicações, somas e subtrações do numerador e denominador. Depois a fração e só por último você aplica esse quadrado que está aí fora dos colchetes.
Vamos lá:
Agora só nos resta fazer essa potência. Pra isso a gente aplica o quadrado em cima e embaixo:
E assim achamos o valor do nosso limite. Eeehhh! 😊
Obs.: uma coisa importante que temos que ver é o seguinte, você poderia substituir diretamente o valor do por na função diretamente, desde o início da resolução. Dessa forma aqui:
O que torna nossa resolução bem mais simples e direta. Mas isso só é possível de ser feito por causa de todas as propriedades que mostramos na resolução. Então, se você pegou bem o que as propriedades nos permitem fazer, você pode substituir diretamente, sem medo de errar. Mas atenção! É sempre importante você entender as regras, ok?
Resposta
Exercício Resolvido #10
Calcule o limite:
Passo 1
Fala aí, vamos ver mais alguns propriedades dos limites com esse exercício aqui que parece ser bem cabeludo, mas que na verdade nós vamos deixar ele bem mais simples de resolver.
Antes, vamos fazer um combinado! Quando uma questão parecer difícil, você respira fundo e olha pra ela com calma tentando simplificar ao máximo sua resolução. Ok?

O que o enunciado pede pra gente é para determinar para qual valor a função se aproximará quando nós fizermos o tender a .
Pra entendermos bem o que faremos, vamos olhar com calma para o limite.
Veja que a função que está ali é uma fração, e essa fração ainda está dentro de uma raiz cúbica.
Para resolver esse limite faremos uso de algumas propriedades que vão deixar tudo bem mais simples. Vamos ver a primeira no próximo passo.
Passo 2
Bom, a primeira propriedade que iremos usar, diz pra gente que quando temos uma função dentro de uma raiz, nós podemos passa o limite pra dentro dela, calcular o limite do que está lá dentro, e só depois resolver a raiz.
Vai ficar assim, ó:
Assim, essa raiz cúbica não será mais um problema pra gente.
Passo 3
Agora vamos olhar o que ficou dentro da raiz. Ficamos com o limite de pra resolver, e como é uma fração, podemos calcular o limite do numerador e do denominador separadamente, e essa é mais uma propriedade dos limites que podemos usar aqui. Assim, ficamos com:
Show, ainda dá para melhorar um pouco mais.
Passo 4
Agora repara que em cada um desses limites que sobraram, temos funções polinomiais com vários termos. Uma outra propriedade dos limites diz pra gente que podemos calcular o limite de cada termo separadamente e depois juntarmos tudo. Além disso, ainda podemos colocar o que for constante pra fora do limite multiplicando na frente dele. Com isso transformamos nosso limite:
Em:
Maravilha, agora chegou a hora de resolver de fato o limite!
Passo 5
Perceba que o que fizemos foi transformar o limite que era:
Em
E assim poderemos aplicar o limite em cada pedacinho separadamente. Pra isso a gente retira o operado e substitui o valor de por em todos os lugares que aparecer o . Aí ficaremos com:
Com isso, só nos resta resolver essa expressão que sobrou. Lembrando sempre de resolver primeiro as potências de dentro, depois as multiplicações, somas e subtrações do numerador e denominador, e só por último você tira a raiz cúbica do que sobrou.
Vamos lá:
Primeiro as potências. Como são potências de base negativa , nós olhamos os expoentes. Quando o expoente for par, a potências terá resultado positivo, e quando for ímpar, terá resultado negativo. Assim e , ficando com:
Agora as multiplicações:
Somas e dubitações:
Agora só nos resta encontrarmos a raiz cúbica dessa fração que sobrou. Pra isso a gente aplica a raiz em cima e embaixo:
Você se lembra qual o valor que quando multiplicamos por ele mesmo 3 vez, dá como resultado o ? Esse valor é o , porque .
E qual o valor que multiplicado por ele mesmo vezes, tem como resultado o ? Esse valor é o próprio , porque Com isso:
E assim achamos o valor do nosso limite. Eeehhh! 😊
OBS.: Você poderia substituir o valor do por na função diretamente, desde o início da resolução. Dessa forma aqui:
O que torna nossa resolução bem mais direta. Mas isso só é possível de ser feito por causa de todas as propriedades que mostramos na resolução. Então, se você pegou bem o que as propriedades nos permitem fazer, você pode substituir diretamente, sem medo de errar. Mas atenção! É sempre importante você entender as regras, ok?