Assíntota oblíqua
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí, você acaba de chegar no Responde Aí! E vamos falar agora sobre assíntota oblíqua!
Então, confere essa nossa videoaula sobre o tema:
Assíntotas oblíquas
Uma assíntota oblíqua acontece quando o gráfico de uma curva tende a se alinhar com uma reta inclinada, como mostra na imagem:
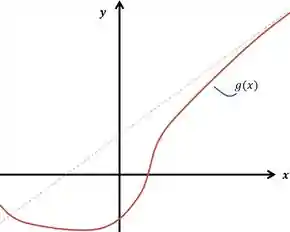
Ou seja, quando
Assim como nas assíntotas horizontais, uma função só pode ter, no máximo, duas assíntotas oblíquas: uma para
Como achar uma assíntota oblíqua?
O objetivo aqui é encontrar a equação da reta da assíntota.
Por definição a equação de uma reta é
Como podemos ver, precisamos de
Super de boas, não é mesmo!? Então vamos continuar e fazer uns exercícios 👇