Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.1 - Ex. 8
8 -
Passo 1
O valor próprio é a raiz da equação característica do . Aqui, é qualquer matriz e denota a matriz de identidade. Se o valor for positivo, o ponto crítico será instável; se o valor for negativo, o ponto crítico será assintoticamente estável. E se o valor é puramente imaginário, o ponto crítico é estável.
Passo 2
Considere o sistema:
a)
Vamos assumir como a solução do sistema. Portanto iremos substituir esse valor no sistema.
Passo 3
Os valores são as raízes da equação.
Portanto, os autovalores são e .
Passo 4
Quando , a equação fornece,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é: .
Passo 5
Quando , a equação fornece,
Cada linha gera a condição:
O autovetor correspondente ao autovalor é: .
Passo 6
b) Como os valores encontrados são reais, desiguais e têm o mesmo sinal, o ponto crítico é um nó. Agora, os dois autovalores são de sinal negativo; o ponto crítico é um nó assintoticamente estável.
Passo 7
c) O plano de fase do diferencial fornecido pode ser desenhado abaixo:
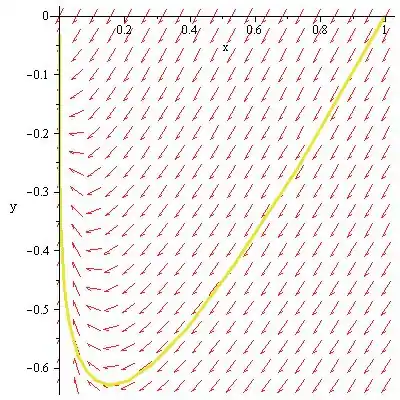
Resposta
- Os autovalores são e .
- O ponto crítico é um nó assintoticamente estável.
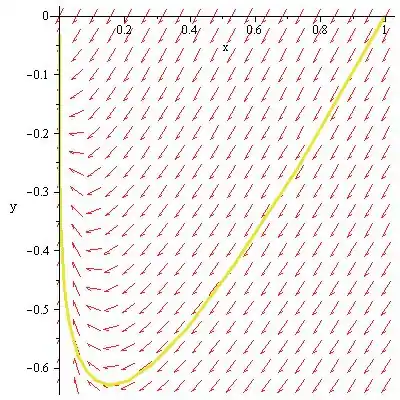
O autovetor correspondente ao autovalor é:
O autovetor correspondente ao autovalor é: