Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 4.2 - Ex. 1
1-10. Esboce o gráfico de onde
1.
Passo 1
Show de bolinhas galera, queremos expressar o gráfico da função definida por partes onde
Iradoso né galera, só aquele módulo ali que tá meio feio. Vamos fazer o seguinte, vamo pegar ele, fritar ele e fazer purê dele hahah brincadeirinha, vamos abrir esse módulo e ver se ele é isso tudo mesmo. Saca só, queremos o (módulo de ), quando ele se aproxima de 1, ou seja,
Logo podemos reescrever a função por partes como
Tá começando a ficar bonito hehehe
Passo 2
Show de bola, isso quer dizer que a gente pode separar essa função em 3 casos de acordo com os intervalos, a nossa funçãozinha está variando em função de , MAAAAASSSS a funçãozona está variando em função de , isso quer dizer que o domínio do nosso espaço está em , por esse motivo devemos separar os intervalos de , da mesma maneira que os intervalos de , e integrá-los separadamente. Saca só:
Se , temos que e .
Se , temos que
E se vamos ter que
Portanto, podemos definir como
Passo 3
Agora é só a gente pegar essa função definida por partes e esboçar o gráfico dela de acordo com os intervalos. Então para o primeiro intervalo, temos que e , logo
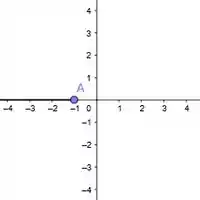
Se , temos que , e o gráfico no intervalo é
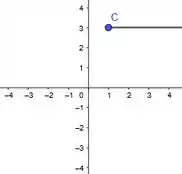
E se , e o gráfico fica no intervalo é
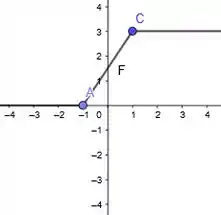
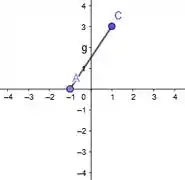
Portanto, junto todos esses gráficos, temos que o gráfico de será
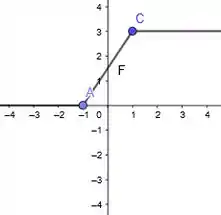
Agora tamo de boinhas fala memo hehehe
Resposta
