Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.5 - Ex. 20
14.20. Utilize o grafo da árvore para escrever a Regra da Cadeia para o caso dado. Assuma que todas as funções sejam diferenciáveis.
, onde ,
Passo 1
Vamos lá, o exercício pede para gente usar o grafo da árvore para escrever a Regra da Cadeia das funções, e para fazer isso, primeiro a gente precisa fazer o nosso grafo da árvore.
Repare que no topo da nossa árvore está , e se separa em e , pois então começa assim
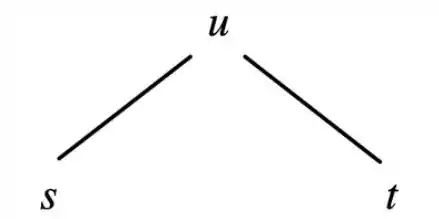
Mas o exercício diz também que é uma função de e também é uma função de
Então
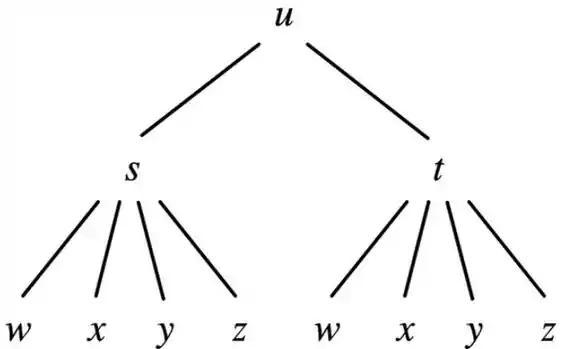
Passo 2
Agora a gente tem nossa árvore, fica mais fácil escrever a regra da cadeia, vamos derivar em relação à .
Começando por , essa derivada vai ser a mesma coisa que a derivada de em relação a multiplicado pela derivada de em relação a somado com a derivada de em relação a multiplicado pela derivada de em relação a .
Como é função de explicitamente, assim como também é, sabemos fazer essas derivadas.
Seguindo a mesma lógica
E por fim
Reparou que a única diferença entre as equações é uma letra?