Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.4 - Ex. 34

Ache a área da região limitada pela curva

y = x 2 - 9 x 2

pelo eixo x e pela reta x = 5 .

Passo 1

Primeiro passo é identificar que área é essa, né? Mas desenhar o gráfico dessa função é complicado e, na verdade, nem precisamos, pois essa é uma função positiva, pessoal. Nesse caso, ao calcular a integral em certo intervalo, o resultado é justamente a área!

Mas qual seria o nosso intervalo? O problema disse que a área é limitada pela curva, pelo eixo x e a reta x = 5 , então vamos ver onde essa função corta o eixo x no primeiro quadrante para descobrir o limite inferior da integral. Para isso, nós vamos igualar a função a 0 .

x 2 - 9 x 2 = 0   →         x 2 - 9 = 0           x = ± 3

Pronto, descobrimos que o limite inferior da integral será x = 3 , considerando apenas o primeiro quadrante. Vamos dar uma olhada no gráfico só para confirmar.

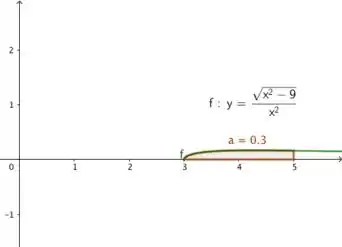
Passo 2

Agora, de acordo com os dados anteriores, a área será dada pela integral:

A = ∫ 3 5 x 2 - 9 x 2 d x

Podemos resolver essa integral de duas formas: calcular a indefinida e no final resolver a definida ou ir resolvendo direto trocando os limites de integração.

Nesta questão, nós vamos resolver a definida, no caminho, trocando os limites de integração, ok? Agora, para resolver, vamos precisar saber qual substituição trigonométrica usar.

Como nós temos a expressão x 2 - 9 = x 2 - 3 2 , isso indica a substituição com a secante, como vocês podem ver a seguir no quadro de substituições com os respectivos triângulos e intervalos.

Olhando o quadrinho, percebemos que a substituição deve ser x = 3 sec ⁡ θ .

Passo 3

Façamos então a substituição:

x = 3 sec ⁡ θ d x = 3 sec ⁡ θ tan ⁡ θ d θ

Dessa forma, x 2 = 9 sec 2 ⁡ θ     →     x 2 - 9 = 9 sec 2 ⁡ θ - 9 = 9 sec 2 ⁡ θ - 1 ⏞ tan 2 ⁡ θ = 3 2 tan 2 ⁡ θ .

Passo 4

Agora vamos trocar a variável da integral, mas antes vamos obter os limites de integração na variável θ . Seja então:

x = 3 → 3 = 3 sec ⁡ θ →           1 = sec ⁡ θ     →         θ = 0 x = 5 → 5 = 3 sec ⁡ θ →         θ = sec - 1 ⁡ 5 3

Substituindo na integral:

A = ∫ 3 5 x 2 - 9 x 2 d x = ∫ 0 sec - 1 ⁡ 5 3 3 2 tan 2 ⁡ θ 9 sec 2 ⁡ θ 3 sec ⁡ θ tan ⁡ θ d θ

= 9 9 ∫ 0 sec - 1 ⁡ 5 3 tan ⁡ θ sec ⁡ θ tan ⁡ θ d θ = ∫ 0 sec - 1 ⁡ 5 3 tan 2 ⁡ θ sec ⁡ θ d θ = ∫ 0 sec - 1 ⁡ 5 3 ( sec 2 ⁡ θ - 1 ) ⏞ tan 2 ⁡ θ sec ⁡ θ d θ

= ∫ 0 sec - 1 ⁡ 5 3 sec ⁡ θ - 1 sec ⁡ θ d θ = ∫ 0 sec - 1 ⁡ 5 3 sec ⁡ θ - cos ⁡ θ d θ

Prontinho!

Passo 5

Agora vamos resolver a definida.

Sabemos da integral definida que:

∫ a b f x d x = F b - F a

Em que F é uma primitiva de f .

Dessa forma, utilizando a integral ∫ sec ⁡ θ d θ = ln ⁡ sec ⁡ θ + tan ⁡ θ + C , ficamos com:

A = ∫ 0 sec - 1 ⁡ 5 3 sec ⁡ θ - cos ⁡ θ d θ = ln ⁡ sec ⁡ θ + tan ⁡ θ - sen ⁡ θ 0 sec - 1 ⁡ 5 3

= ln ⁡ sec ⁡ sec - 1 ⁡ 5 3 + tan ⁡ sec - 1 ⁡ 5 3 - sen ⁡ sec - 1 ⁡ 5 3 - ln ⁡ sec ⁡ 0 + tan ⁡ 0 - sen ⁡ 0

O resultado já é esse, mas vamos simplificar.

Passo 6

Para achar tan ⁡ sec - 1 ⁡ 5 3 vamos usar a relação:

tan 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x + 1 = sec 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x = 5 3 2

tan 2 ⁡ sec - 1 ⁡ 5 3 = 25 9 - 1 = 16 9

tan ⁡ sec - 1 ⁡ 5 3 = 4 3     pois       0 ≤ sec - 1 ⁡ 5 3 < π 2

Agora, para achar sen ⁡ sec - 1 ⁡ 5 3 = sen ⁡ sec - 1 ⁡ 5 3 , vamos usar a relação:

sen 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x + cos 2 ⁡ sec - 1 ⁡ 5 3 ⏟ x = 1

sen 2 ⁡ sec - 1 ⁡ 5 3 + 1 sec 2 ⁡ sec - 1 ⁡ 5 3 = 1

sen 2 ⁡ sec - 1 ⁡ 5 3 + 1 5 3 2 = 1

sen 2 ⁡ sec - 1 ⁡ 5 3 + 9 25 = 1

sen 2 ⁡ sec - 1 ⁡ 5 3 = 1 - 9 25 = 16 25

sen ⁡ sec - 1 ⁡ 5 3 = 4 5         pois       0 ≤ sec - 1 ⁡ 5 3 < π 2

Passo 7

Agora podemos simplificar o resultado achado.

A = ln ⁡ 5 3 + tan ⁡ sec - 1 ⁡ 5 3 - sen ⁡ sec - 1 ⁡ 5 3 - ln ⁡ sec ⁡ 0 + tan ⁡ 0 - sen ⁡ 0

= ln ⁡ 5 3 + 4 3 - 4 5 - ln ⁡ 1 + 0 - 0

A = ln ⁡ 3 - 4 5   u . a

Essa é a área procurada.

Resposta

A = ln ⁡ 3 - 4 5   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área total da região delimitada pela curva y = 2 ln ⁡ x x e o eixo x de x = 1 até y = e .
Determine a área total da região delimitada pela curva x = y 2 3 e pelas retas x = y e y = - 1 .
Determine os valores extremos de f x = x 3 - 3 x 2 e a área da região delimitada pelo gráfico de f e pelo eixo x .
Ache o centroide da região x = 1 a x = π 2 , limitada pela curva y = c o s x e pelo eixo x.
Ache o centroide da região limitada pelo eixo y e pelas curvas y = s e nx - cos ⁡ x e y = s e nx + cos ⁡ x de x = 0 a x = π 2 .