Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 2

2. Um arame tem a forma da curva obtida como interseção da porção da esfera

x 2 + y 2 + z 2 = 4

y ≥ 0

Com o plano

x + z = 2

Sabendo-se que a densidade em cada ponto do arame é dada por

f x , y , z = x y

Calcule a massa total do arame

Passo 1

Oiii. Temos aqui em mãos uma clássica questão de integral de linha em caso escalar. A primeira coisa a fazer é descobrir qual é a nossa curva, afinal temos 3 interseções

x 2 + y 2 + z 2 = 4

y ≥ 0

x + z = 2

O que nos gera a figura abaixo

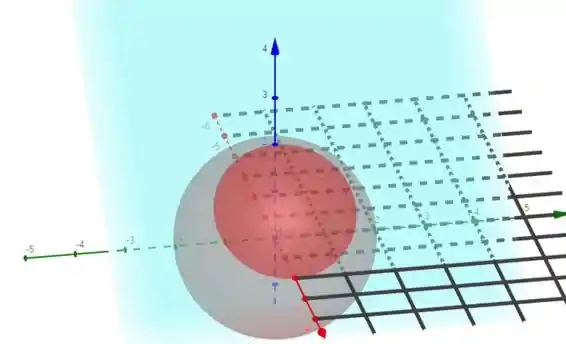
A parte preta tracejada é a parte y > 0 . Entao queremos apenas metade da elipse formada pela interseção de

x 2 + y 2 + z 2 = 4

x + z = 2

Vamos substituir uma equação na outra

z = 2 - x

x 2 + y 2 + 2 - x 2 = 4

x 2 + y 2 + 4 - 4 x + x 2 = 4

2 x 2 - 4 x + y 2 = 0

Se completarmos quadrados teremos

2   x - 1 2 - 2 + y 2 = 0

2 x - 1 2 + y 2 = 2

x - 1 2 + y 2 2 = 1

Logo teremos podemos parametrizar em coordenadas polares

cos ⁡ t = x - 1

x = 1 + cos ⁡ t

Agora vamos descobrir y

sen ⁡ t = y 2

y   = 2 sen ⁡ t

Agora vamos descobrir z

x + z = 2

z = 2 - x  

z = 2 - 1 - cos ⁡ t

  z = 1 - cos ⁡ t  

Com isso nossa parametrização é

σ t = 1 + cos ⁡ t ,   2 sen ⁡ t , 1 - cos ⁡ t

Passo 2

Geograficamente podemos perceber que nossa curva começa em z = 0 ate z = 2 . Vamos então ver o intervalo em t

z = 1 - cos ⁡ t

0 = 1 - cos ⁡ t

cos ⁡ t = 1

t = 0

Vamos ver agora com z = 2

2 = 1 - cos ⁡ t

cos ⁡ t =   - 1

t = π

Beleza!!! Nosso intervalo é

  t ∈ 0 ,   π

Passo 3

Queremos então calcular

∮ c f   d r

Um jeito de calcular isso é parametrizar nossa superfície r

r = σ t

d r = d σ t → σ ' t d t

Como estamos com um campo escalar, não podemos simplesmente plotar o vetor σ ' t d t na integral. Temos que transforma-lo em um escalar

v e t o r → e s c a l a r  

σ ' t d t → σ ' t d t

Então se parametrizarmos essa reta ficamos com

∫ t 0 t 1 f σ t ⋅ | σ ' t |   d t

Beleza!!! Vamos cair dentro \o/

Passo 4

Vamos parametrizar nossa função agora

f x , y , z = x y

f σ t → 1 + cos ⁡ t 2 sen ⁡ t

Beleza agora é calcular | σ ' t |

σ t = 1 + cos ⁡ t ,   2 sen ⁡ t , 1 - cos ⁡ t

σ ' t = - sen ⁡ t , 2 cos ⁡ t , sen ⁡ t

σ ' t = sen 2 ⁡ t + 2 cos 2 ⁡ t + sen ² ⁡ t

σ ' t = 2

Temos tudo o que precisamos para calcular nossa integração

Passo 5

∫ t 0 t 1 f σ t ⋅ σ ' t d t

∫ 0 π 1 + cos ⁡ t 2 sen ⁡ t ⋅ 2   d t

Vamos usar umas identidades trigonométricas para facilitar essa integração

2 ∫ 0 π sen ⁡ t + sen ⁡ 2 t 2   d t

  = 2 - cos ⁡ t - cos ⁡ 2 t 4 0 π

=   2   1 - 1 4 - - 1 - 1 4

= 2   3 4 + 5 4

= 4

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

massa total do arame

= 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4. Calcule ∫ C F ⋅ dr → Ondeh. Fx , y , z = x y , x 2 + z ,y 2 - x e C é a curva de interseção do cone x 2 + y 2 = z 2 ,z0 com o cilindro x = y 2 de 0,0 , 0 a 1,1 , 2
4. Calcule ∫ C F ⋅ dr → Ondeg. Fx , y , z = x 2 - y 2 ,z 2 - x 2 ,y 2 - z 2 e C é a curva de interseção da esfera x 2 + y 2 + z 2 = 4 com o plano y = 1 , percorrida no sentido anti-horario
Encontre a integral de linha de f ( x , y , x ) = 3 / x 2 + y 2 + z 2 sobre a curva r ( t ) = t i + t j + t k , 1 ≤ t ≤ ∞ .
Encontre a integral de linha de f ( x , y , z ) = x + y + z sobre o segmento de reta de ( 1,2 , 3 ) a ( 0 , - 1,1 ) .
Integre f ( x , y , z ) = x + y - z 2 sobre o caminho entre ( 0,0 , 0 ) a ( 1,1 , 1 ) (veja a figura a seguir) dado por: C 1 : r ( t ) = t i + t 2 j ,0 ≤ t ≤ 1 C 2 : r ( t ) = i + j + t k ,0 ≤ t ≤ 1