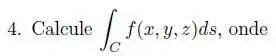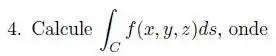Exercícios de Caso Escalar R³ - Lista de Exercícios Resolvida

Encontre a massa de um arame que tem a forma da interseção da esfera e do plano , se a densidade do arame em for .

Calcule , onde é a hélice definida por , .

Calcule

Onde é a hélice .

Seja a curva obtida pela interseção do cilindro elíptico com o plano , satisfazendo . Parametrize a curva e calcule .

Calcule a massa do fio cujo formato é o da curva da interseção das superfícies e , , , com densidade

Integre sobre o segmento de reta que une a origem ao ponto passando primeiro por . Dado a parametrização , .

Calcule

Onde e é a curva interseção das superfícies e situada no primeiro octante.

Calcule

Onde e é a curva interseção das superfícies , com e .

Achar a massa da curva dada por , , , , se a densidade em cada ponto é inversamente proporcional ao quadrado da distância do ponto à origem.

1. Um arame fino é entortado no formato da curva das superfícies e , situado no primeiro octante e que liga o ponto ao ponto . Calcule a massa do arame, sendo a densidade em cada ponto proporcional ao quadrado da distância do ponto ao plano .

Um arame fino tem a forma da curva de interseção das superfícies e , . Determine a massa do arame, se a densidade em qualquer ponto é igual ao quadrado da distância do ponto ao plano .

Seja a interseção das superfícies e A integral e igual a:

Seja uma curva espacial dada pela equação vetorial

(b)Calcule a integral de linha

Calcule a massa da curva dada pela intersecção das superfícies e , com densidade .

1)

1. Calcule a massa do arame com densidade

Sejam

1. Esboce a curva espacial e exiba uma parametrização regular para a mesma.
2. Seja o ponto de cuja coordenada é . Encontre uma parametrização da reta tangente a em .
3. Calcule as equações implícitas da reta tangente a em (i.e, para o valor do parâmetro que corresponde ao ponto ).
4. Calcule a integral de linha

1. Calcule

Onde:

1. e é a interseção das superfícies e , com e , percorrida uma vez do ponto ao .

1. Calcule

Onde:

1. e é a interseção das superfícies e , orientada de modo que sua projeção no plano se percorrida uma vez no sentido horário.

Questão 1: Calcule , onde é dada pela interseção das superfícies , , , , percorrida do ponto ao ponto .

Determine a massa do fio descrito pelas equações e com densidade .

Considere um arame fino com o formato da hélice de parametrização . Calcule o comprimento da curva e a massa do arame, sabendo que a densidade do fio em cada ponto é igual ao quadrado da sua distância à origem.

1) Considere a curva obtida como interseção da superfície com o plano , com :

1. Esboce .
2. Forneça uma parametrização regular de .
3. Calcule a integral de linha:
4. Calcule equações cartesianas da reta tangente a em .

Seja a curva regular espacial dada pela interseção das superfícies

1. Faça o esboço de .
2. Descreva uma parametrização regular de .
3. Calcule as equações implícitas da reta tangente a pelo ponto .
4. Calcule a integral de linha .

Questão 1: Considere a superfície parametrizada , cuja imagem denotaremos por .

a) Calcule uma equação implícita para .

b) Faça um esboço de .

c) é uma superfície parametrizada regular ou não? Justifique a resposta.

d) Calcule a equação implícita do plano tangente a no ponto .

e) Calcule a integral de superfície .

Seja a curva interseção da semiesfera , com o plano . Determine o valor de , se

Um pedaço de arame tem a forma da curva interseção da esfera como plano . Calcule a massa do arame se a densidade é dada por .

Questão 1) Seja o arco da curva

Cujo ponto de início é e o seu ponto de término é .

1. Determinar uma parametrização lisa da curva .
2. Determinar o comprimento da curva .

Questão 3) Sabendo que um arame tem o formato da curva

Seja , a função densidade linear do arame. Determine a massa do arame.

Questão 1: Calcule a integral de linha

Onde é o trecho da intersecção das superfícies e , do ponto ao ponto e que está contido no semi-espaço .

Considere a curva definida por

com .

1. Encontre as equações paramétricas da reta tangente à curva no ponto correspondente a .
2. Escreva a integral que representa o comprimento de .

Calcule a integral de linha

Onde a curva é descrita por , , , como .

Seja . Calcular a integral da função sobre a curva definida por , onde varia no intervalo .

Quando uma curva , passa pelo domínio de uma função no espaço, os valores de ao longo da curva são dados pela função composta . Quando integramos essa função composta em relação ao comprimento de arco de a , calcula-se a integral de linha de ao londo da curva.

Portanto .

Calcule a integral de linha onde é a hélice circular dada por , .

Seja . Calcular a integral da função sobre a curva definida por onde varia no intervalo .

Calcule

Onde e é a interseção do cilindro parabólico com a parte do plano , tal que .

Seja a curva parametrizada , .

1. Qual a distância, menor possível, do ponto da curva para ao ponto da curva para ?
2. Considere uma partícula de massa desprezível que percorre a curva . Qual seria a distância percorrida sobre a curva para a partícula ir do instante até o instante ?

Calcule a integral de linha , onde é dada pela função vetorial .

Calcule a integral de linha , onde é dada pela função vetorial .

6) Seja

Verifique se é conservativo e em qual domínio. Se for, obtenha um potencial tal que

Seja a curva regular dada pela interseção das superfícies

a) Faça um esboço das superfícies e da curva regular .

b) Descreva uma parametrização regular de (

c) Calcule as equações implícitas da reta tangente à parametrização , onde a componente atinge seu máximo.

d) Calcule a integral de linha.

Questão 1: Seja a curva regular obtida pela interseção das superfícies cujas equações implícitas são e , e tal que que .

1. Esboce cuidadosamente as superfícies e , destacando explicitamente os pontos de contato de com o plano .
2. Determine uma parametrização regular para .

(Dica: Tente com uma parametrização da forma )

3. Calcule , para a função escalar

Calcule a massa do arame com formato , onde é a curva obtida pela interseção das superfícies

Com densidade .

Considere a curva definida pela parametrização

com .

4) Calcule o comprimento do arco de curva de correspondente ao intervalo .

Calcule onde é a parte da interseção do plano com a superfície , , de ponto inicial e final .

Considere a superfície S definida pela parametrização

Com

1. Encontre uma equação cartesiana para a superfície S. Faça um esboço.
2. Escreva o elemento de superfície dS para S e a integral usada para o cálculo da área S.
3. Determine a equação do plano tangente a S no ponto definido por (2,3,0).

Questão 3: Calcule a integral de linha

Onde a curva é definida na seguinte maneira: