11 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
Além disso, considere a equação:
Se o valor de , então o valor de é:
Se o valor de , em seguida, os valores de e é:
Portanto, os pontos críticos são:
,
Passo 2
b)
O gráfico de direção é mostrado abaixo:
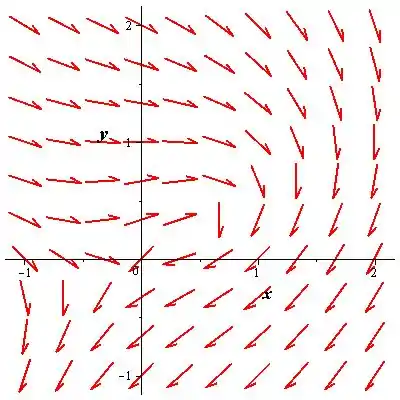
O gráfico de direção é mostrado abaixo:
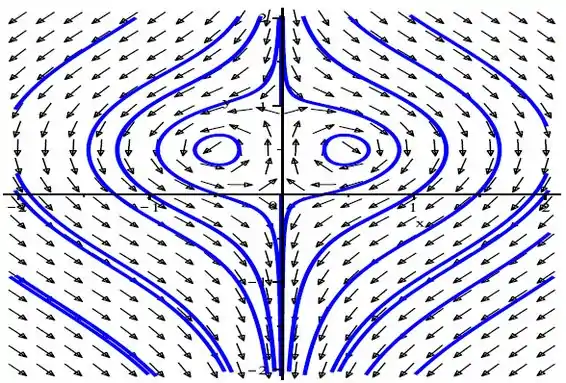
Passo 3
c) Observe o gráfico de direção na parte acima.
O ponto crítico é um ponto de sela e é instável.
O ponto crítico é um ponto de sela.
Portanto, o ponto crítico é um ponto de sela instável.
O ponto crítico é um centro.
Portanto, o ponto crítico é um centro e é assintoticamente estável.
O ponto crítico é um centro.
Portanto, o ponto crítico é um centro e é assintoticamente estável.
Passo 4
d) Observe o gráfico de direção na parte acima b.
O ponto crítico assintoticamente estável é e .
Portanto, a bacia de atração de cada ponto crítico e consiste no restante do plano .
Resposta
- Os pontos críticos,
- O gráfico de direção é mostrado abaixo:
- O ponto crítico é um ponto de sela.
- O ponto crítico assintoticamente estável é e .
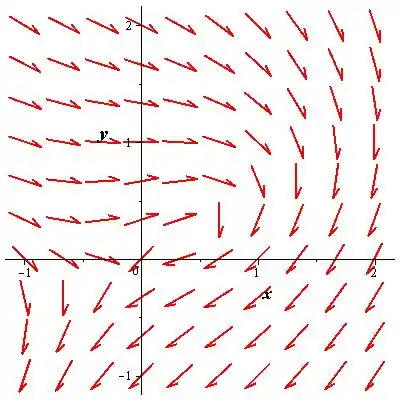
O gráfico de direção é mostrado abaixo:
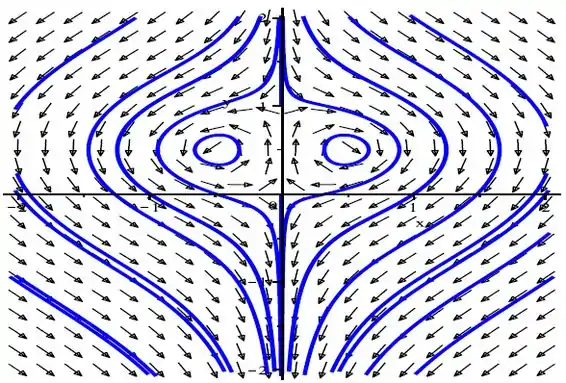
Portanto, o ponto crítico é um ponto de sela instável.
O ponto crítico é um centro.
Portanto, o ponto crítico é um centro e é assintoticamente estável.
O ponto crítico é um centro.
Portanto, o ponto crítico é um centro e é assintoticamente estável.
Portanto, a bacia de atração de cada ponto crítico e consiste no restante do plano .