Sistemas de EDO

Nessa página, nós do Responde Aí, estamos focados em te mostrar uma introdução sobre os Sistemas de Equações Diferenciais Ordinárias (EDO)

Conhecimentos Prévios

Bom, para que você entenda bem os sistemas de EDO ou Equações Diferenciais Ordinárias (muito melhor falar só EDO, não é? hahaha) é necessário que você saiba e conheça as EDOs no geral, o que elas são, como identificá-las, etc.

Então, é importante você conhecer previamente esses dois assuntos aqui:

✅ EDO de 1° Ordem

✅ EDO de 2° Ordem

Caso ainda tenha dúvidas, pausa a leitura dessa página, vai dar uma conferida nesses assuntos listados e depois retorna pra cá, combinado?

Sistema de EDO

Lembra lá no ensino médio que você tinha que resolver um sistema de equações pra encontrar o valor de e por exemplo?

Nós tínhamos duas variáveis, e , duas equações e quando resolvíamos esse sistema, chamado sistema de equações, nós tínhamos como resultado um valor para e outro para , correto?

Aqui temos um caso bem parecido, nós temos um sistema de equações, porém as equações envolvidas são equações diferenciais ordinárias, ou seja, EDOs.

Lembra que quando resolvíamos uma EDO nós obtinhamos uma função que obedecia aquela equação? A principal diferença entre um sistema de equação "normal" e o sistema de EDO é que ao resolver o sistema de EDO, nós encontramos funções como resultado e não um valor para uma variável.

Então, vamos supor que temos uma função, denominada por , e outra denominada por . Nós queremos descobrir quem são essas funções e a informação que temos é duas EDO que envolvem essas funções:

Para acharmos essas funções, temos que resolver esse sistema. Esse sistema de EDO é dito um sistema de EDO de primeira ordem porque só estão envolvidas EDOs de primeira ordem, beleza?

Uma coisa bem importante em sistemas de EDOs é saber escrevê-los na notação matricial. A cara de um sistema de EDO de primeira ordem na forma matricial é essa aqui:

Vamos ver rapidinho o que é cada coisa nessa equação aí, pegando como exemplo o sistema que vimos aí em cima.

será o vetor com as derivadas que aparecem nas equações. No nosso caso:

O vetor vai ser o vetor das funções, então:

Agora, será a matriz de coeficientes das funções que estão envolvidas nas equações, assim:

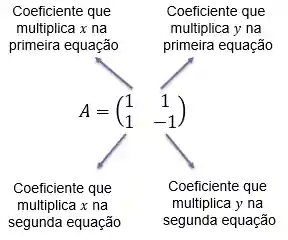
E por último, o vetor será o vetor da parte não homogênea das equações, onde temos a variável escrita explicitamente. No nosso caso fica assim:

Então, nosso sistema na forma matricial fica assim:

Poo, bem interessante, mas você pode estar se perguntando: Como eu resolvo esse sistema?

É isso que será explorado dentro do assunto Sistemas de EDO aqui no Responde Aí. É isso que você está precisando saber? Então não perca a oportunidade de continuar aqui com a gente e aprender isso.

Aqui nessa página nós mostramos pra você uma introdução breve do que é o sistema de EDO e como representá-lo na forma de matrizes. O conteúdo completo sobre esse assunto foi separado em capítulos e tópicos para você estudar de forma bem organizada, e nele nós abordamos os métodos de resolução e muitos outros aspectos. Confere nosso Raio-X aqui em baixo 👇🏽 e não perca a oportunidade de aprender com a plataforma de exatas que foi criada para salvar o seu semestre! 😉