Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.8 - Ex. 9
Em cada um dos problemas de 7 a 10:
(a) Encontre a solução do problema de valor inicial dado.
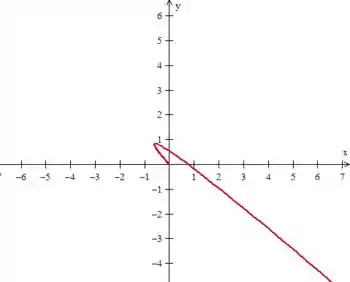
(b) Desenhe a trajetória da solução no plano e desenhe, também, o gráfico de em função de .
9.
Passo 1
Beleza! Vamos então resolver esses sistema de EDO linear. Para isso, aqui está a matriz de coeficientes retirada do nosso sistema:
E agora encontrar os seus autovalores !
Bem, como é apenas subtrair da diagonal principal...
Resolvendo o determinante...
Resolvendo por Báskara...
A solução de um sistema de EDO com real e único:
Onde e são:
Onde . e são os autovalores determinados a partir de:
Vamos então determinar esse autovetor !
Passo 2
Primeiro o autovalor :
Então para o teremos de coordenadas desconhecidas :
Ora, sabemos que asta subtrair da diagonal:
Essas duas linhas são Linearmente dependentes e sempre serão! Então, basta pegar a primeira linha e multiplicar com a coluna e igualar a (produto de matrizes):
Se falarmos que , então...
Então um autovetor para é:
Primeiro o autovalor :
Então para o teremos de coordenadas desconhecidas :
Ora, sabemos que asta subtrair da diagonal:
Essas duas linhas são Linearmente dependentes e sempre serão! Então, basta pegar a primeira linha e multiplicar com a coluna e igualar a (produto de matrizes):
Se falarmos que , então...
Então um autovetor para é:
Passo 3
Onde e são:
Então...
Beleza! Então chegamos aqui na solução do nosso sistema! Bora encontra a solução particular dada os valores iniciais...
Passo 4
Esses valores iniciais significam que...
Então substituindo o por ...
Resolvendo esse sisteminha em ...
Beleza! Agora é só substituir e simplificar:
Passo 5
Usando algum aplicativo de plotagem de gráficos (por exemplo, o winplot), podemos plotar o gráfico de implicitamente em funções de :
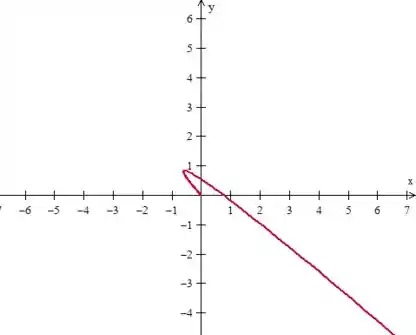
E para o gráfico de em função de ...
Resposta
Letra A:
Letra B:
