Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.1 - Ex. 10
Em cada um dos problemas de 1 e 12:
(a) Desenhe um campo de direções para a equação diferencial dada.
(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores grandes de t.
(c) Encontre a solução geral da equação diferencial dada e use – a para determinar o comportamento das soluções quando
Passo 1
Discutimos até esse ponto do livro como resolver alguns casos mais simples de EDO, a partir de agora vamos começar a lidar com equações que tem a seguinte cara:
O método para resolver tal equação que vamos utilizar é conhecido como método do fator integrante.
Dada uma equação no formato acima o que devemos primeiramente fazer é deixar a equação assim ó:
Passo 2
a)
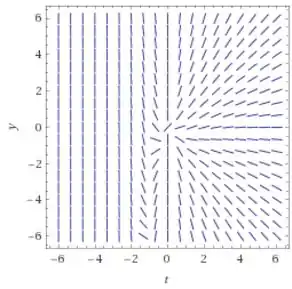
b) Para
Passo 3
c) Trabalhando em cima do nosso problema, vamos resolver pelo método...
Multiplicamos por
De modo que
Integrando nosso resultado acima( nesse passo, não incluímos a constante de integração ):
Repare que o lado esquerdo da nossa equação que foi multiplicada por é o resultado da regra do produto de derivação de 2 funcões
Subsituindo os valores encontrados e integrando
Para