Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 56
Calcule o ângulo entre a diagonal de um cubo e e a diagonal de uma de suas faces.
Passo 1
Pra facilitar nossas vidas, vamos pensar num cubo unitário, posicionado no primeiro ocutante, de modo que seu canto traseiro esquerdo esteja na origem e suas bordas estejam ao longo dos eixos coordenados , .
Assim:
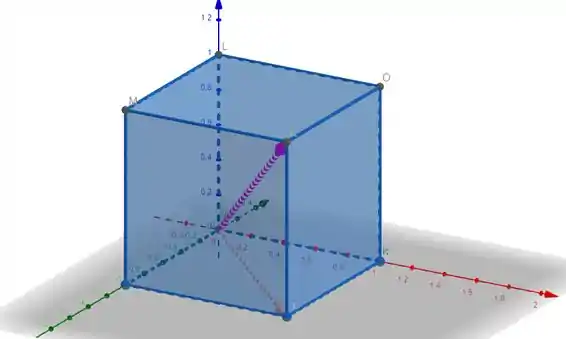
Esse vetor rosinha que eu desenhei dentro dele é uma diagonal. Ela começa na origem e termina no ponto , portanto, é o vetor
Esse outro vetor vermelhinho que eu desenhei é o vetor diagonal da face que tá no plano . Ele começa na origem e termina no ponto , portanto, é o vetor
Podemos dizer que o ângulo formado entre esses dois vetores é .
Passo 2
Dito isso, o ângulo entre dois vetores pode ser calculado por
Vamos então calcular esse produto escalar do numerador e o modulo dos vetores do denominador:
Passo 3
Substituindo tudo na formula:
Assim,