Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.4 - Ex. 3

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green.

∮ C x y   d x + x 2 y 3 d y

C é o triangulo com vértices 0,0 ,   1,0 e 1,2

Passo 1

Fala, meus amigos! Tranquilo?

Nossa questão pede a integral de linha

∮ C x y   d x + x 2 y 3 d y

Em que C é o triangulo com vértices 0,0 ,   1,0 e 1,2 .

A parte a) quer o método direto. Nele vamos ter que dividir C em três partes de forma que C = C 1 ∪ C 2 ∪ C 3 , onde cada parte é uma reta que liga um ponto ao outro, de forma que

∮ C F ⋅ d r = ∫ C 1 F ⋅ d r 1 + ∫ C 2 F ⋅ d r 2 + ∫ C 3 F ⋅ d r 3

Onde F = ( x y , x 2 y 3 )

E resolver cada integral de linha separadamente, usando a parametrização adequada para cada um dos 4 segmentos.

Já para a parte b) vamos usar o Teorema de Green:

∫ C P   d x + Q   d y = ∬ ∂ Q ∂ x - ∂ P ∂ y d A

Onde P é nossa função integrada em d x e Q é nossa função integrada em d y . Então vamos calculas as derivadas parciais dessas funções, substituir na equação do Teorema de Green e resolver nossa integral dupla resultante da forma que já sabemos.

Bora lá!

Passo 2

  1. Como C é um triangulo, vamos ter que dividir C em três partes de forma que C = C 1 ∪ C 2 ∪ C 3 , onde cada parte é uma reta que liga um ponto ao outro, de forma que

    2. ∮ C F ⋅ d r = ∫ C 1 F ⋅ d r 1 + ∫ C 2 F ⋅ d r 2 + ∫ C 3 F ⋅ d r 3

    Onde F = ( x y , x 2 y 3 )

    Colocando os quatro pontos no plano para ficar claro de quais retas precisamos

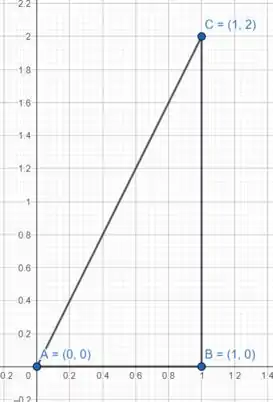
    Para que a orientação seja positiva, precisamos da reta de ( 0,0 ) a ( 1,0 ) .

    Precisamos inicialmente definir qual será a função r t . A parametrização da reta é calculada por:

    r t = P 1 + t P 2 - P 1

    Os pontos da nossa reta são:

    P 1 = ( 0,0 )

    e

    P 2 = ( 1,0 )

    Então:

    r t = 0 , 0 + t 1 , 0 - 0 , 0

    Subtraindo os pontos:

    r t = 0 , 0 + t 1 , 0

    Somando finalmente, temos:

    C 1 : r 1 t = t , 0 ,   0 ≤ t ≤ 1

    Derivando:

    d r 1 = r 1 ' t = 1,0

    E a integral é

    ∫ C 1 F ⋅ d r 1 = ∫ 0 1 t ⋅ 0 , t 2 0 3 ⋅ 1,0   d t

    Fazendo o produto escalar, chegamos na integral de zero!

    ∫ C 1 F ⋅ d r 1 = ∫ 0 1 0   d t = 0

    Passo 3

    Outra reta sai de ( 1,0 ) e vai até ( 1,2 ) que tem parametrização de processo igual à que fizemos no passo 2.

    C 2 : r 2 t = 1,2 t ,   0 ≤ t ≤ 1

    Derivando:

    r 2 ' t = 0,2

    E a integral é

    ∫ C 2 F ⋅ d r 2 = ∫ 0 1 2 t , 1 2 2 t 3 ⋅ 0,2   d t

    Fazendo o produto escalar:

    = ∫ 0 1 2 4 t 3   d t = 16 t 4 4 0 1

    Aplicando os limites de integração:

    ∫ C 2 F ⋅ d r 2 = 16 4 = 4

    Por fim temos a reta que vai de ( 1,2 ) até a origem, fechando a curva C . Parametrizando como no passo 2:

    C 3 : r 3 t = 1 - t , 2 - 2 t ,   0 ≤ t ≤ 1

    r 3 t = 1 - t , 2 1 - t

    Derivando essas equações paramétricas:

    d r 3 = r 3 ' t = - 1 , - 2

    Substituindo na integral:

    ∫ C 3 F ⋅ d r 3 = ∫ 0 1 1 - t 2 1 - t , 1 - t 2 2 1 - t 3 ⋅ - 1 , - 2   d t

    Fazendo o produto escalar:

    = ∫ 0 1 - 2 1 - t 2 - 2 4 1 - t 5   d t

    Integrando em t :

    = 2 3 1 - t 3 + 16 6 1 - t 6 0 1

    Podemos aplicar os limites de integração:

    ∫ C 3 F ⋅ d r 3 = - 2 3 - 8 3 = - 10 3

    Então temos que

    ∮ C F ⋅ d r = ∫ C 1 F ⋅ d r 1 + ∫ C 2 F ⋅ d r 2 + ∫ C 3 F ⋅ d r 3

    = 0 + 4 - 10 3 = 2 3

    Então:

    ∮ C F ⋅ d r = 2 3

    Passo 4

  2. Pelo Teorema de Green temos que

∮ C x y   d x + x 2 y 3 d y = ∬ D ∂ ∂ x x 2 y 3 - ∂ ∂ y x y d A

Calculando as derivadas parciais:

= ∬ D 2 x y 3 - x   d A

Analisando D podemos usar D = x , y 0 ≤ x ≤ 1 ,     0 ≤ y ≤ 2 x }

= ∫ 0 1 ∫ 0 2 x 2 x y 3 - x   d y d x

Integrando por dentro, primeiro em y , tratando x como constante:

= ∫ 0 1 x y 4 2 - x y 0 2 x   d x

Aplicando os limites:

= ∫ 0 1 8 x 5 - 2 x 2   d x

Agora é só integramos em x :

= 8 x 6 6 - 2 x 3 3 0 1 = 8 6 - 2 3

= 4 3 - 2 3 = 2 3

Então:

∮ C F ⋅ d r = 2 3

Prontinho! Veja que chegamos no mesmo resultado pelos dois métodos!

Resposta

2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 1-4, verifique a conclusão do teorema de Green calculando ambos os lados das Equações 3 e 4 para o campo F = M i + N j . Tome os domínios de integração em cada caso como sendo o disco R
Nos Exercícios 19 e 20, encontre o trabalho realizado por F paramover uma partícula uma vez em sentido anti-horário ao redor dacurva dadaF = (4x – 2y)i + (2x – 4y)jC: A circunferência (x – 2)2 + (y –
Nos Exercícios 1-4, verifique a conclusão do teorema de Green calculando ambos os lados das Equações 3 e 4 para o campo F = M i + N j . Tome os domínios de integração em cada caso como sendo o disco R
Nos Exercícios 1-4, verifique a conclusão do teorema de Green calculando ambos os lados das Equações 3 e 4 para o campo F = M i + N j . Tome os domínios de integração em cada caso como sendo o disco R
Aplique o teorema de Green para calcular as integrais nos Exercí-cios 21-24 ∮ C y 2 d x + x 2 d y C: O triângulo limitado por x = 0 , x + y = 1 , y = 0 .