Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.7 - Ex. 18
Calcule a integral tripla.
, onde é limitado pelo cilindro e pelos planos , e no primeiro octante
Passo 1
A equação , representa um círculo no plano , onde é uma constante qualquer, já que a equação não depende de , então é como de pegássemos a circunferência e esticássemos ela de menos infinito até mais infinito, formando um cilindro de altura infinita com centro sendo o eixo , ou .
Então se isolarmos
Podemos pegar a variação como sendo , agora analisando as outras equações, e e a outra restrição é o máximo valor de na equação , que acontece quando , onde , então no plano temos
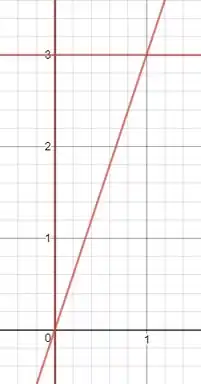
Podemos botar a variação como sendo e .
Passo 2
Resolvendo a integral, temos
Agora calculando a integral dupla
Resposta
Exercícios de Livros Relacionados
Calculem) int int int_B e^(x^2) * d x * d y * d z onde B é o conjunto 0 = x = 1 , 0 = y = x e 0 = z = 1 .
Calculee) int int int_B d x * d y * d z onde B é o conjunto x^2 + y^2 = z = 2 * x .
Calculeg) int int int_B d x * d y * d z onde B é o conjunto x^2 + y^2 = z = 2 * x + 2 * y - 1
Calculel) int int int_B x * d x * d y * d z onde B é o conjunto x^2 - y^2 = z = 1 - 2 * y^2 .
Calculen) int int int_B x * d x * d y * d z onde B é o conjunto x^2 = y = x , 0 = z = x + y .