Uma companhia de sopa deseja fabricar uma lata na for- ma de um cilindro circular reto que tenha capacidade para 500 cm3 de líquido. O material para a tampa e a base custa 0,02 centavos/cm2 , enquanto o material para a lateral custa 0,01 centavos/cm2

(a) Estime o raio r e a altura h da lata que custa menos para ser fabricada. [ Sugestão: Expresse o custo C em termos de r.]

(b) Suponha que a tampa e a base de raio r sejam tiradas de folhas quadradas, cujos lados têm comprimento 2r, e os retalhos são descartados. Levando em conta o custo das folhas quadradas, você esperaria que o custo da lata mais barata seja maior ou menor do que em (a)? Explique.

(c) Estime o raio, a altura e o custo da lata em (b) e determine se sua conjectura estava certa.

É aí que entra o volume! Queremos que o cilindro tenha de capacidade. Então, esse deve ser o nosso volume! E como calculamos o volume de um cilindro? Produto da área da base com a altura, certo? Assim:

E, como já vimos ali em cima até, a área da base do cilindro é a área de um círculo:

Como nosso volume deve ser :

E, para achar a relação entre a altura e o raio, vamos isolar a altura nessa equação:

Substituindo isso na fórmula do custo do passo 1:

Simplificando e multiplicando o 500 com o 0,02:

Para saber as dimensões do cilindro mais barato, vamos plotar o gráfico do custo e ver qual o valor de que minimiza esse custo. Mas antes vamos lembrar que, como é uma medida de comprimento, não teremos valores de negativos!! O gráfico do custo fica, então:

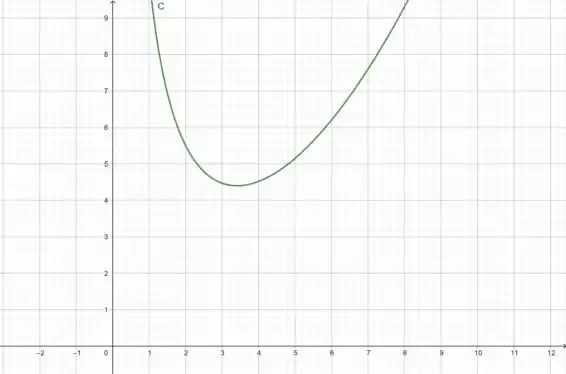
Bom, com isso, a gente vê que o valor de que minimiza o custo está entre e . Vamos pegar, então, , ok? O custo será em torno de centavos.

Se , a altura será:

Então, essas são as dimensões do cilindro mais barato: e .

(b) Temos como resolver essa questão sem fazer uma conta. Só pensar o seguinte:

Se eu vou usar esses quadrados para pegar minha base e minha tampa, eles devem ter uma área maior do que minha base e minha tampa. Senão vai faltar material! Porque aí minha base seria maior que o quadrado, ou seja, o quadrado não seria suficiente para construir minha base.

Dessa forma, como a área do quadrado deve ser maior, o custo também será maior do que o esperado em (b).

Se você não acredita em mim, vou usar as contas para te mostrar que isso é verdade:

Temos um quadrado de lado , logo, sua área será .

E, para esse quadrado, temos uma base de raio , sua área é

Por comparação, como , que é menor que , . Mas você pode substituir o valor de que encontramos no passo anterior e verificar isso também! Isso vai acontecer para a tampa também, pois a área da tampa é igual a da base e o quadrado também não muda.

E, se temos uma área maior, temos um custo maior, logo, levando em consideração os quadrados, o custo seria maior!

(c) O raio e a altura, já sabemos, serão os mesmos de (a). Para saber o custo, precisamos calcular a soma dos custos com a lateral e com a base e a tampa.

O custo da lateral será:

E, como cada custa 0,01 centavo:

O custo base e da tampa será o custo de duas folhas quadradas:

E, como cada custa 0,02 centavo:

Com isso, o custo total será:

Comparando com o valor do passo 3 ( centavos), vemos que o custo realmente aumentou.