Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.1 - Ex. 3
Considere um triângulo Isósceles situado no semiplano y e com a base paralela ao eixo x. Mostre que o volume do sólido obtido pela rotação deste triângulo, em torno do eixo x, é igual ao produto da área deste triângulo pelo comprimento da circunferência gerada, na rotação, pelo baricentro do triângulo.
Passo 1
Primeiro temos que entender o que está sendo dito na questão.
Se sabemos que o triângulo tem a base paralela ao eixo x e ele é isósceles, então podemos desenhá-lo dessa maneira:
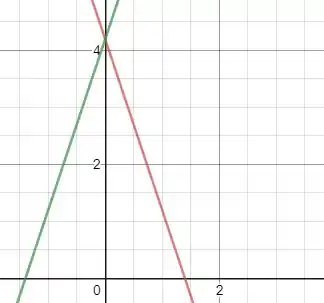
Gráfico para duas função de modelo
No desenho dá pra perceber que cada reta lateral do triângulo se parece com uma reta do tipo , ou seja, , sendo e
Se calcularmos o m com dois pontos conhecidos como os pontos em que cortam o eixo x e o eixo y, teremos os pontos (0, y0) e (xf, 0) e teremos:
Com isso temos o valor de y, que vai ser importante na hora de calcularmos tanto o volume como a área da figura, assim y é:
Beleza, agora sabemos o que é o triângulo e como escrevê-lo matematicamente, mas o que ele quer?
Ele quer saber se duas coisas são iguais, assim encontramos essas coisas isoladamente e vemos se os resultados batem!
Essas coisas são:
- O volume do sólido obtido pela rotação deste triângulo, em torno do eixo x;
- O produto da área deste triângulo pelo comprimento da circunferência gerada, na rotação, pelo baricentro do triângulo.
Mão na massa!
Passo 2
Pra calcular o volume do sólido obtido pela rotação deste triângulo, em torno do eixo x usamos:
Sendo y=f(x) e lembrando que essa função só descreve metade do triângulo , temos que multiplicar a função por 2 antes de aplicar, ficamos com:
Passo 3
Sabemos que a área de um retângulo é:
Sendo a base do triângulo xf e a altura y0 temos que:
Porém como são dois triângulos:
O baricentro de um triângulo isósceles é um terço da altura, então ficamos que no fim O produto da área deste triângulo pelo comprimento da circunferência gerada, na rotação, pelo baricentro do triângulo é:
Isso se dá por que consideramos o baricentro como raio e fazemos a rotação, assim o é multiplicado por 2 para conseguirmos a circunferência.
Passo 4
Com isso concluímos que ambos são iguais:
Resposta
Ei, a resposta está no passo a passo :)