1. Construir os gráficos das funções quadráticas . Dar o domínio e conjunto imagem.

1. , se

O que essas funções tem em comum?

Elas seriam o que chamamos de família de parábolas que passam pelo centro, pois para todas essas funções

Para, temos que a função parte do , tem concavidade para cima, pois

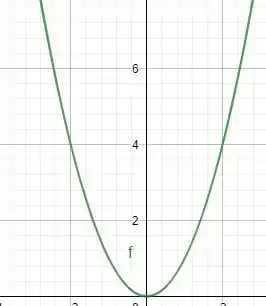
Outra coisa que eu disse que retiraríamos do gráfico, é o conjunto imagem, você consegue perceber qual é a imagem? Ou seja, quais o valores que esse gráfico consegue “alcançar” em .

Caso não tenha a resposta! Eu te digo de qualquer forma, mas são apenas os valores maiores que zero, com o zero incluso, ou seja:

Vamos para o próximo valor e faremos a mesma coisa!

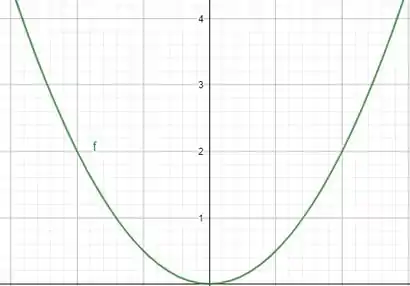
Para , temos que a função é escrita como e parte do tente lembrar que todas elas vão partir desse ponto! Tem concavidade para cima, porém quando . O gráfico dela seria assim:

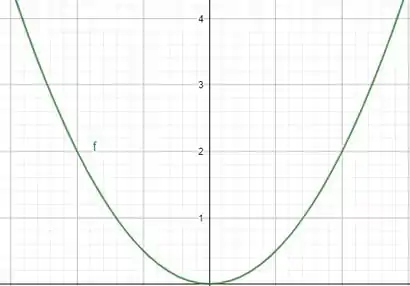
Vamos retirar desse gráfico a imagem e como você está analisando, a imagem são os valores de para cima!

Então:

Estamos indo para a última!!

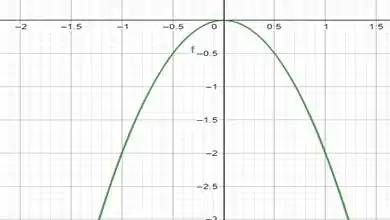
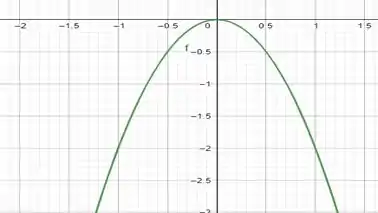
Vamos lá, na última teremos a diferença de que o número é negativo!

Para , temos que .

As características dessa função são, a concavidade é para baixo, assim como todas as funções anteriores, ela passa pelo e quando , temos que . Construindo esse gráfico:

Assim como nas outras funções, iremos determinar a imagem a partir do gráfico! E se você entendeu como achamos o conjunto imagem antes, você vai conseguir obter agora!

Ora, o conjunto imagem são apenas os números negativos, olha lá no gráfico, a parábola parte do e só vai para baixo!