Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.7 - Ex. 14

Converta a integral:

∫ - 1 1 ∫ 0 1 - y 2 ∫ 0 x x 2 + y 2 d z d x d y

Em uma integral equivalente em coordenada cilíndricas e calcule o resultado

Passo 1

Faaaala, cara! Tranquileba?

Vamos olhar o gráfico para que fique mais fácil de entendermos

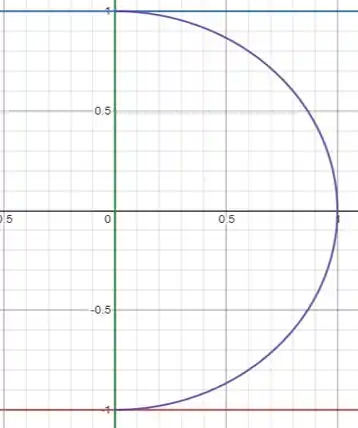
E lembremo-nos das coordenadas cilíndricas f ( r , θ , z )

Onde temos que:

x = r cos ⁡ θ

y = r   s e n θ

r 2 = x 2 + y 2

E com isso já conseguimos verificar no gráfico que:

0 ≤ r ≤ 1

- π 2 ≤ θ ≤ π 2

E se z = x   no superior z = r cos ⁡ θ

E dada função de demonstração x 2 + y 2 temos que é igual a r 2 , assim:

∫ - π 2 π 2 ∫ 0 1 ∫ 0 r c o s θ r 2 d z   r   d r   d θ

Onde o r adicional é o Jacobiano das coordenadas cilíndricas, que nos permite fazer essa transformação

Passo 2

∫ - π 2 p i 2 ∫ 0 1 ∫ 0 r cos ⁡ θ r 3 d z   d r   d θ

∫ - π 2 π 2 ∫ 0 1 r 3 z 0 r cos ⁡ θ d r   d θ

∫ - π 2 π 2 ∫ 0 1 r 4 cos ⁡ θ d r   d θ

∫ - π 2 π 2 cos ⁡ θ 5 r 5 0 1   d θ

Passo 3

1 5 ∫ - π 2 π 2 cos ⁡ θ d θ

1 5 s e n θ - π 2 π 2

2 5

Resposta

2 5

Exercícios de Livros Relacionados

Encontre os volumes dos sólidos nos Exercícios 43-48.
Cilindro e planos Encontre o volume da região delimitadapelo cilindro x2 + y2 = 4 e os planos z = 0 e x + y + z = 4.
Cilindro e paraboloide Encontre o volume da região delimitada inferiormente pelo plano z = 0, lateralmente pelo cilindrox2 + y2 = 1 e superiormente pelo paraboloide z = x2 + y2.
Encontre os volumes dos sólidos nos Exercícios 43-48.
Paraboloide e cilindro Encontre o volume da região delimitada superiormente pelo paraboloide z = 9 – x2 – y2, inferiormente pelo plano xy e fora do cilindro x2 + y2 = 1.