Derivada de . Represente graficamente a função para . Depois, na mesma tela, faça o gráfico de
Para e. Experimente outros valores de , incluindo valores negativos. O que acontece ? Explique este comportamento.
Passo 1
Esta é uma questão que necessita de recursos tecnológicos. Precisamos obter os gráficos de múltiplas funções para entender o que acontece a medida em que diminuímos o valor de . Além disto, a questão nos diz para testar outros valores aleatórios de , a fim de que tenhamos certeza do que ocorre com a função. Esta intepretação vai surgir naturalmente a partir do momento em que observarmos as curvas. Entretanto, para poder explicar melhor o fenômeno por trás, vamos relembrar como obtemos a derivada de uma função pela definição. Para isto, calculamos o seguinte limite:
Agora que relembramos este conceito, vamos direto as contas!
Passo 2
O nosso ponto de partida é obter o gráfico das funções e o gráfico da função
Quando ; e . Sendo assim, temos:
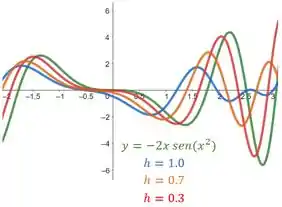
Passo 3
A medida em que diminuímos o valor de , podemos ver que as curvas da função se aproxima da curva da função . Inicialmente, temos a sensação de que, quando ,
Passo 4
Vamos confirmar o que acontece quando e um número bem próximo de . Para isto, vamos fazer e. Sendo assim, temos o seguinte gráfico:
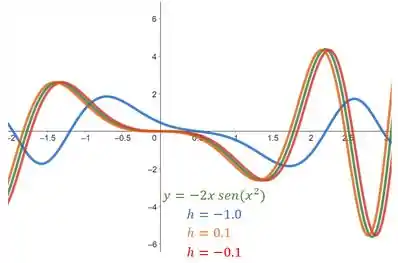
Passo 5
Confirmamos agora que a nossa função nada mais é que a definição de derivada. Inclusive, a curva em que encontra-se totalmente sobreposta do gráfico da função . Portanto, quando , temos a derivada da função , que é a função .
Resposta
Quando , temos a derivada da função , que é a função .